#105 从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]返回如下的二叉树:
3
/
9 20
/
15 7题解
- 递归
- 递归+HashMap确定树根、栈的方式
- 更清晰的图解过程
- 相似题:106. 从中序与后序遍历序列构造二叉树,可用相同模板AC。
- 在递归方法中,传入数组的切片实际是将数组复制了一次。改进方案为传入子数组的边界索引。(来自106题解)
模板
class Solution(object):
def buildTree(self, preorder, inorder):
"""
:type preorder: List[int]
:type inorder: List[int]
:rtype: TreeNode
"""
if len(inorder) == 0:
return None
# 前序遍历第一个值为根节点
root = TreeNode(preorder[0])
# 因为没有重复元素,所以可以直接根据值来查找根节点在中序遍历中的位置
mid = inorder.index(preorder[0])
# 构建左子树
root.left = self.buildTree(preorder[1:mid+1], inorder[:mid])
# 构建右子树
root.right = self.buildTree(preorder[mid+1:], inorder[mid+1:])
return root#120 三角形最小路径和
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[ [2], [3,4], [6,5,7], [4,1,8,3]]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
说明:
如果你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分。
题解
- 三角形最小路径和 :自底向上的动态规划,最终结果为
dp[0][0],递推式dp[i,j] = min(dp[i+1,j],dp[i+1][j+1])+dp[i,j]。 - 优化:因为只需要下层的结果,将二维dp数组降为一维dp数组。
- 优化:直接将triangle数组替换成dp数组(原地dp),不会对结果造成影响,省下了dp数组的空间。
- 自顶向下动态规划也可以,但是需要特殊判断的情况更多,首元素和尾元素均需要特判;而自底向上就不会有这样的问题。
- 相似题: 62. 不同路径 、 63. 不同路径 II
模板
动态规划的模板主要注意两点
- 先写出递推式
- 注意递推式中下标的边界
#152 乘积最大子序列
给定一个整数数组 nums ,找出一个序列中乘积最大的连续子序列(该序列至少包含一个数)。
示例 1:
输入: [2,3,-2,4] 输出: 6 解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: [-2,0,-1] 输出: 0 解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
题解
- 动态规划。维护一个dp数组,分别保存到该位置为止最大值和最小值(用来放负数)。当前的最大最小值只可能从三个数中产生,即
dp[i-1][0] * nums[i],dp[i-1][1] * nums[i]和nums[i],类比于最大子序列和中要么选当前元素,要不不选。最后结果为dp[i][0] - 优化:其实动态规划的过程只需要用到上一步的最大最小值,因此将二维数组降为两个数保存
imax,imin,但是注意这两个数在更新时时独立的,在更新其中一个的过程中会用到另一个值,比如先更新imax,再更新imin的过程中用到imax时,需要用没更新之前的imax,所以需要一个临时变量保存未更新之前的imax。 - 双向遍历。分情况讨论:
- 若数组全是正数,答案即为所有元素乘积。
- 若数组中负数为偶数,答案同上。
- 若数组中负数为奇数,则答案要么不包含最左边的负数,要么不包含最右边的负数。
- 若数组中有0,则乘到该位置时会让后续的结果都变为0,所以将max置为1,继续上述过程,等于把0跳过去了。
#84 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
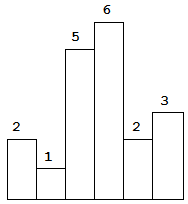
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
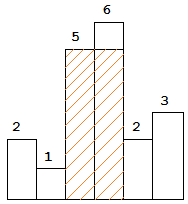
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3] 输出: 10
题解
- 柱状图中最大的矩形
- 暴力:找所有两个柱子形成的面积,面积取决于两个柱子之间最矮的柱子。
- 优化暴力:数组保存上述的最矮柱子的高度。
minheight[j]表示从第j个柱子开始到当前的柱子,最矮的高度是多少。 - 分治:最大面积存在三种情况,取当前所有柱子中最矮的作切分。
- 优化分治:针对排序数组,用线段树。
- 栈:
模板
分治算法:
public class Solution {
public int calculateArea(int[] heights, int start, int end) {
// 边界情况
if (start > end)
return 0;
// 找到当前分区内最矮的柱子
int minindex = start;
for (int i = start; i <= end; i++)
if (heights[minindex] > heights[i])
minindex = i;
// 合并最优解,三种情况:最优解在左子问题,最优解在右子问题,最优解在合并左右问题
return Math.max(heights[minindex] * (end - start + 1),
Math.max(calculateArea(heights, start, minindex - 1),
calculateArea(heights, minindex + 1, end)));
}
public int largestRectangleArea(int[] heights) {
return calculateArea(heights, 0, heights.length - 1);
}
}栈法:
class Solution(object):
def largestRectangleArea(self, heights):
"""
:type heights: List[int]
:rtype: int
"""
# -1 进栈
stack = [-1]
max_area = 0
# 对于每个柱子height[i]
for i in range(len(heights)):
# 如果当前高度比栈顶高度小
while stack[-1] != -1 and heights[i] <= heights[stack[-1]]:
# 栈顶元素出栈
pop_ind = stack.pop()
# 新栈顶元素
top_ind = stack[-1]
# 高度为栈顶元素高度,宽度为新栈顶元素到当前位置的上一个位置的下标之差
area = heights[pop_ind] * (i - top_ind - 1)
# 更新最大面积
max_area = max(area, max_area)
# 如果height[i] 比栈顶高度大,直接进栈
# 如果height[i] 比栈顶高度小,经过上面的出栈操作后,将现在的柱子进栈
stack.append(i)
# 到达数组末端,此时栈并不为空,做最后一次比较,相当于在最后进栈了0,因为0肯定比任何元素都小,所以又做了一次上面的当前高度比栈顶高度小的情况。
while stack[-1] != -1:
pop_ind = stack.pop()
top_ind = stack[-1]
area = heights[pop_ind] * (len(heights) - top_ind -1)
max_area = max(max_area, area)
return max_area#85 最大矩形
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
输入: [ ["1","0","1","0","0"], ["1","0","1","1","1"], ["1","1","1","1","1"], ["1","0","0","1","0"] ] 输出: 6
题解
- 最大矩形 (转化为84题的解法)
- 详细通俗的思路分析,多解法
- 更直白一点的动态规划 (思路可以,代码和图可能有问题)
- c++单调栈解法 (更为清晰的解法)
- 精妙解法,位运算 (跪着看的解法)