15. Scipy Tutorial- 快速傅立叶变换fft
傅立叶变换是数字信号处理领域一种很重要的算法。要知道傅立叶变换算法的意义,首先要了解傅立叶原理的意义。
傅立叶原理表明:任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号,以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。
因此,可以说,傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号(信号的频谱),可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅立叶反变换将这些频域信号转换成时域信号。
从现代数学的眼光来看,傅里叶变换是一种特殊的积分变换。它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换$(dft)$。
快速傅氏变换$(fft)$是离散傅氏变换$(dft)$的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是进了一大步。$fft$的计算结果和$dft$是完全等价的,只是运算量降低了。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。
用$dft$对模拟信号进行谱分析,只能是近似的,其近似程度取决于信号带宽、采样频率和截取长度。采样定理告诉我们,如果以超过函数最高频率的两倍的取样率来获得样本,连续的带限函数可以完全地从它的样本集来恢复。采样频率为$F_s$,信号频率为$F$,采样点数为$N$,频域抽样间隔为$F_0$,即频率分辨力。模拟信号经过A/D转换变为数字信号的过程称为采样。为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的2倍,这称之为采样定理。
假设采样频率为fs,采样点数为N,那么FFT结果就是一个N点的复数,每一个点就对应着一个频率点,某一点n(n从1开始)表示的频率为:fn=(n-1)*fs/N。
举例说明:用1kHz的采样频率采样128点,则FFT结果的128个数据即对应的频率点分别是0,1k/128,2k/128,3k/128,…,127k/128 Hz。
傅里叶变换在图像处理领域的应用是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。换句话说,傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数。傅里叶逆变换是将图像的频率分布函数变换为灰度分布函数。
import numpy as np
import matplotlib.pyplot as plt
def signal_samples(t):
return np.sin(1 * np.pi * t) + np.sin(2 * np.pi * t) + np.sin(4 * np.pi * t)
B = 5.0
f_s = 2 * B
delta_f = 0.01
N = int(f_s / delta_f)
T = N / f_s
t = np.linspace(0, T, N)
f_t = signal_samples(t)
fig, axes = plt.subplots(1, 2, figsize=(8, 3), sharey=True)
axes[0].plot(t, f_t)
axes[0].set_xlabel("time (s)")
axes[0].set_ylabel("signal")
axes[1].plot(t, f_t)
axes[1].set_xlim(0, 5)
axes[1].set_xlabel("time (s)")
plt.show()
from scipy import fftpack
F = fftpack.fft(f_t)
f = fftpack.fftfreq(N, 1.0/f_s)
mask = np.where(f >= 0)
fig, axes = plt.subplots(3, 1, figsize=(8, 6))
axes[0].plot(f[mask], np.log(abs(F[mask])), label="real")
axes[0].plot(B, 0, 'r*', markersize=10)
axes[0].set_ylabel("$\log(|F|)$", fontsize=14)
axes[1].plot(f[mask], abs(F[mask])/N, label="real")
axes[1].set_xlim(0, 2.5)
axes[1].set_ylabel("$|F|$", fontsize=14)
axes[2].plot(f[mask], abs(F[mask])/N, label="real")
axes[2].set_xlabel("frequency (Hz)", fontsize=14)
axes[2].set_ylabel("$|F|$", fontsize=14)
plt.show()
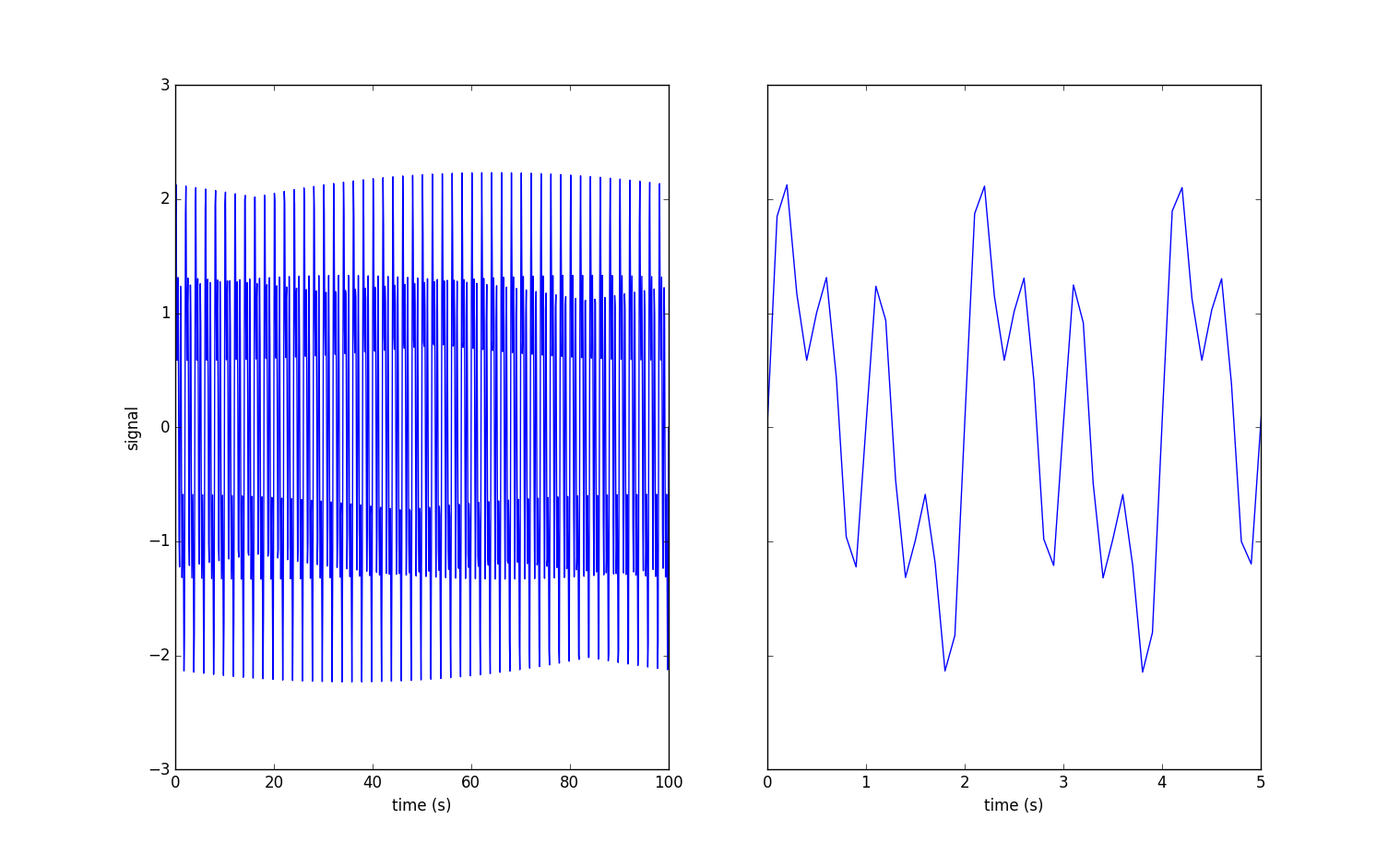
程序有两次图像输出,第一次是绘制时域的信号:由频率为2Hz、1Hz和0.5Hz的正弦波组成。
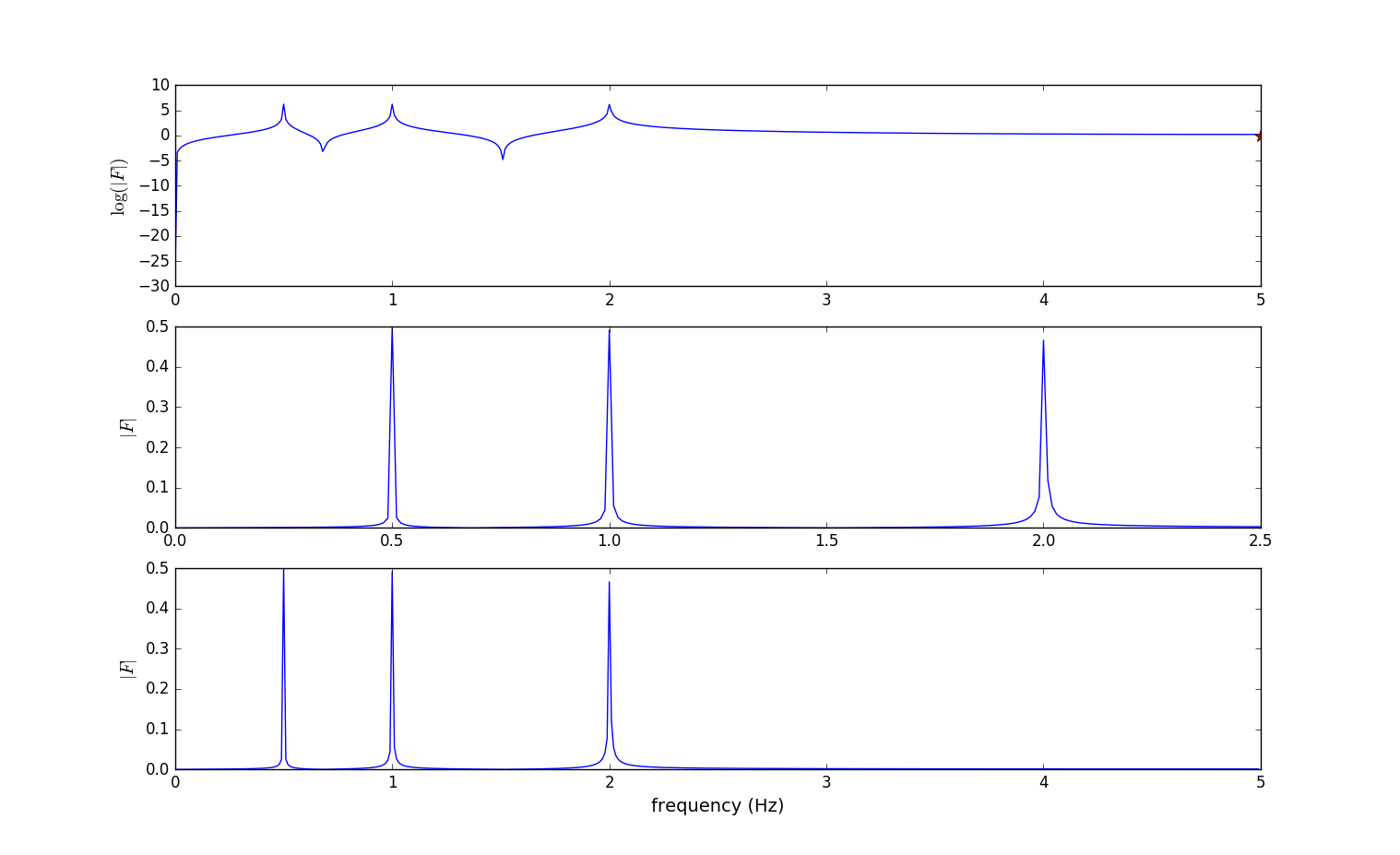
第二次输出的是经fft转化的频域图。
从两张图可以看出时域信号很难分析、看清楚信号的特征,而经fft处理后的频率信号可以清晰的看出有3个频率的(正弦)波。
(1). 定义可以生成离散时域信号的函数$signal_samples$:
$$
y = \sin(\pi t) +\sin(2\pi t) + \sin(4\pi t)
$$
对应频率分别为$2Hz$、$1Hz$和$0.5Hz$、
import numpy as np
import matplotlib.pyplot as plt
def signal_samples(t):
return np.sin(1 * np.pi * t) + np.sin(2 * np.pi * t) + np.sin(4 * np.pi * t)
(2). 下面定义的是采样率等信息。$\odot$由于定义的产生时域信号的函数signal_samples里的正弦函数的频率最大是$2Hz$所以依据采样定理,采样率大于信号中最高频率成分的2倍,那么$f_s > 2 * 2 = 4$即可,为了可视化化更清晰些,可以设定$\ \ f_s = 10Hz\ $。$\odot$设置频谱(frequency spectrum)精度$\Delta f = 0.01Hz$,$\odot$那么需要的采样点的个数$N = \frac{f_s}{\Delta f} = \frac{10}{0.01} = 1000$个。$\odot$需要在$T = \frac{N}{f_s} = \frac{1000}{10} = 100s $秒完成(采用时间)。
B = 5.0
f_s = 2 * B
delta_f = 0.01
N = int(f_s / delta_f)
T = N / f_s
(3). 采样时域信号。$t$表示从$100$秒内共1000个采样点(时间点)。连续信号经采样变成离散信号。
t = np.linspace(0, T, N)
f_t = signal_samples(t)
t传给函数signal_samples生成时域上的信号$f_t$的采样数据共1000个。
(4). 绘制时域信号f_t的可视化图。
t = np.linspace(0, T, N)
f_t = signal_samples(t)
fig, axes = plt.subplots(1, 2, figsize=(8, 3), sharey=True)
axes[0].plot(t, f_t)
axes[0].set_xlabel("time (s)")
axes[0].set_ylabel("signal")
axes[1].plot(t, f_t)
axes[1].set_xlim(0, 5)
axes[1].set_xlabel("time (s)")
plt.show()
(5). 时域信号经fft处理后转化为频率信号数据。scipy的fftpack包里的fft函数可以将采样得到的离散信号从时域转为频域的数据。而fftfreq函数可以求得各个采样点的频率值。
from scipy import fftpack
F = fftpack.fft(f_t)#参数为时域信号
f = fftpack.fftfreq(N, 1.0/f_s)#参数为采样点数和周期
mask = np.where(f >= 0)
实信号频谱是对称的,单边谱就代表了这个信号的全部信息,所以用mask来过滤掉频谱的负半轴数据。
(6). 绘制频率信号可视化图。
fig, axes = plt.subplots(3, 1, figsize=(8, 6))
axes[0].plot(f[mask], np.log(abs(F[mask])), label="real")
axes[0].plot(B, 0, 'r*', markersize=10)
axes[0].set_ylabel("$\log(|F|)$", fontsize=14)
axes[1].plot(f[mask], abs(F[mask])/N, label="real")
axes[1].set_xlim(0, 2.5)
axes[1].set_ylabel("$|F|$", fontsize=14)
axes[2].plot(f[mask], abs(F[mask])/N, label="real")
axes[2].set_xlabel("frequency (Hz)", fontsize=14)
axes[2].set_ylabel("$|F|$", fontsize=14)
plt.show()
可视化图中间的图在频率为$2Hz$、$1Hz$、$0.5Hz$处出现了峰值(peak)对应于函数$signal_samples$里的各个正弦波的频率。
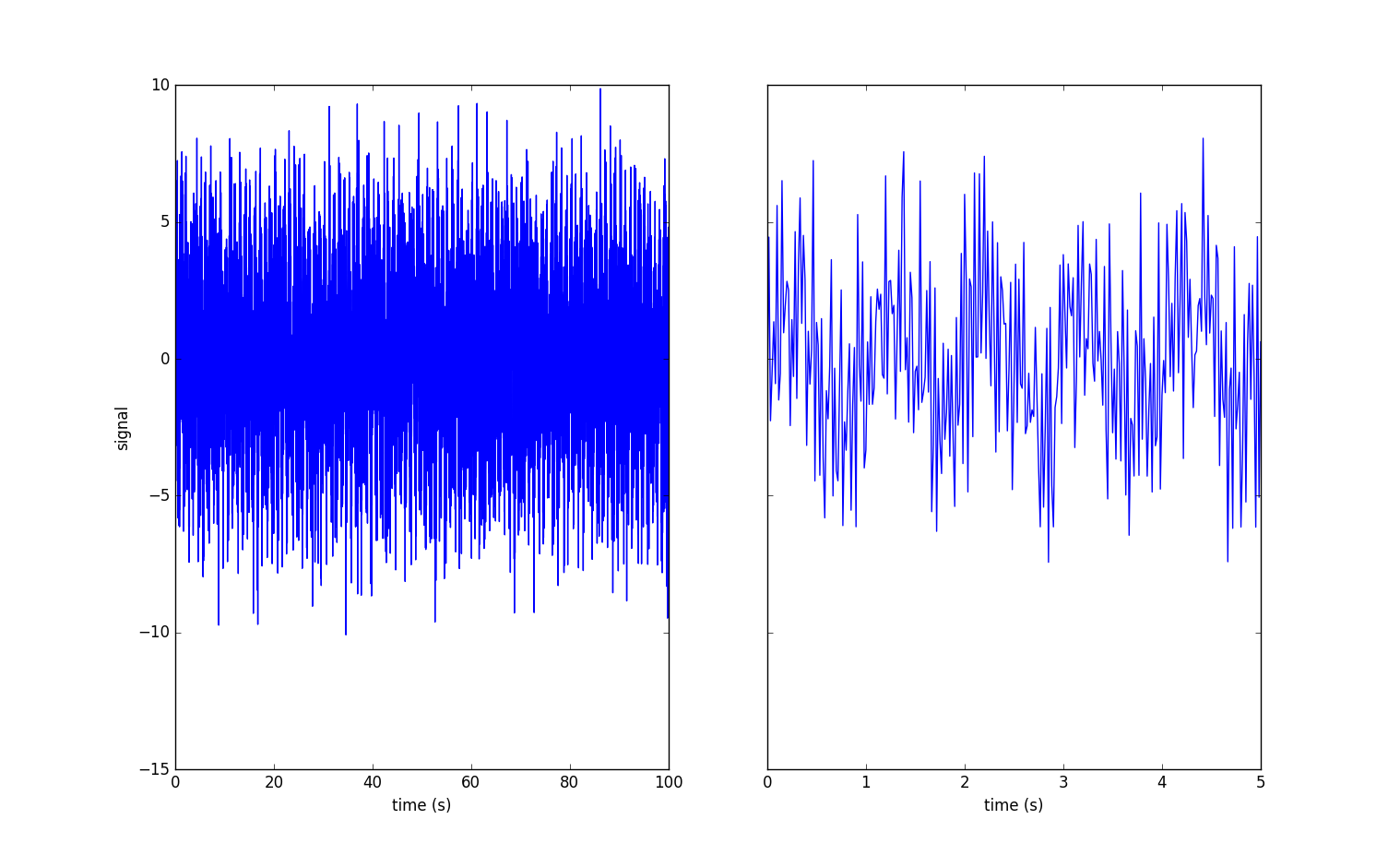
加噪声。前面的例子里的信号是干净的信号,这里对$signal_samples$进行简单的处理,增加一点儿噪声,看看fft的用处如何?
def signal_samples(t):
return (2 * np.sin(2 * np.pi * t) + 3 * np.sin(22 * 2 * np.pi * t) + 2 * np.random.randn(*np.shape(t)))
这里的np.random.randn(*np.shape(t)))产生噪声,信号里只有两个正弦波。
import numpy as np
import matplotlib.pyplot as plt
def signal_samples(t):
return (2 * np.sin(2 * np.pi * t) + 3 * np.sin(22 * 2 * np.pi * t) + 2 * np.random.randn(*np.shape(t)))
B = 30.0
f_s = 2 * B
delta_f = 0.01
N = int(f_s / delta_f)
T = N / f_s
t = np.linspace(0, T, N)
f_t = signal_samples(t)
fig, axes = plt.subplots(1, 2, figsize=(8, 3), sharey=True)
axes[0].plot(t, f_t)
axes[0].set_xlabel("time (s)")
axes[0].set_ylabel("signal")
axes[1].plot(t, f_t)
axes[1].set_xlim(0, 5)
axes[1].set_xlabel("time (s)")
plt.show()
from scipy import fftpack
F = fftpack.fft(f_t)
f = fftpack.fftfreq(N, 1.0/f_s)
mask = np.where(f >= 0)
fig, axes = plt.subplots(3, 1, figsize=(8, 6))
axes[0].plot(f[mask], np.log(abs(F[mask])), label="real")
axes[0].plot(B, 0, 'r*', markersize=10)
axes[0].set_ylabel("$\log(|F|)$", fontsize=14)
axes[1].plot(f[mask], abs(F[mask])/N, label="real")
axes[1].set_xlim(0, 2.5)
axes[1].set_ylabel("$|F|$", fontsize=14)
axes[2].plot(f[mask], abs(F[mask])/N, label="real")
axes[2].set_xlim(21, 23)
axes[2].set_xlabel("frequency (Hz)", fontsize=14)
axes[2].set_ylabel("$|F|$", fontsize=14)
plt.show()
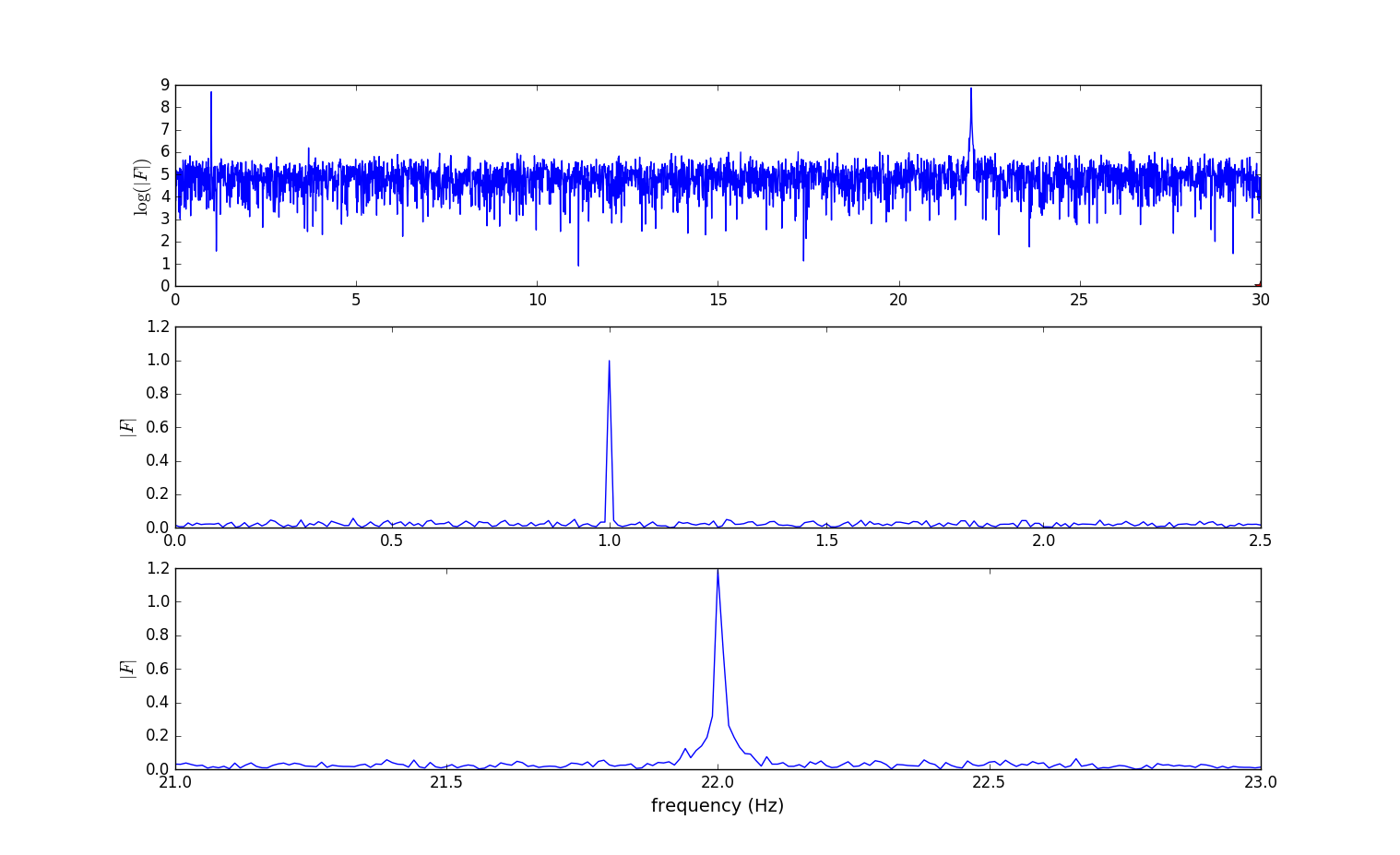
程序里的采用率修改了,代码其他部分基本没有太大的变化。
这幅图能看出啥?下面的频谱图最上面的子图能看出在频率为$1Hz$和$22Hz$处出现了峰值,对应于signal_samples函数里的两个正弦波的频率。