前言

读本文前，你应该有基本的圆锥曲线知识，能够应对中等难度的题目；能够熟练运用韦达定理等传统方法解题；且有一定的数学功底。阅读本文后，你可以尝试自己推导所有结论，并形成较为系统的笔记，方便以后复习。

强烈推荐GeoGebra这款数学绘图软件。本文所有图片均由GeoGebra绘制。

---

极坐标

PS：写这篇文章的时候我还没学极坐标和参数方程，所以难免有不太规范的地方（比如

极坐标下，若把圆锥曲线的焦点放在极点，则圆锥曲线的统一方程为：

下面以椭圆为例（抛物线、双曲线类似）：

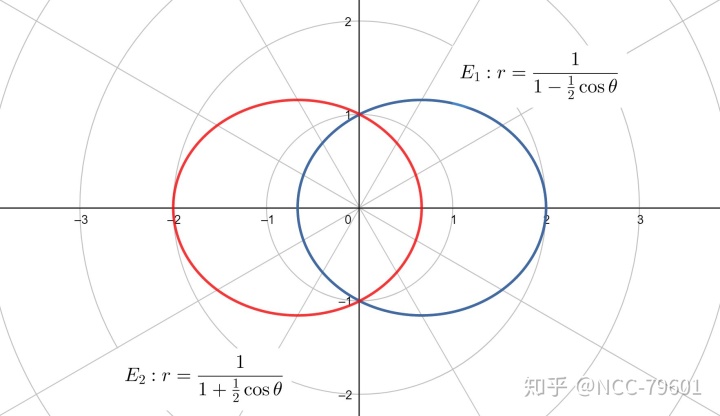
可以看出， 此处的正负号并不影响圆锥曲线的形状，只影响圆锥曲线的位置。

推导：

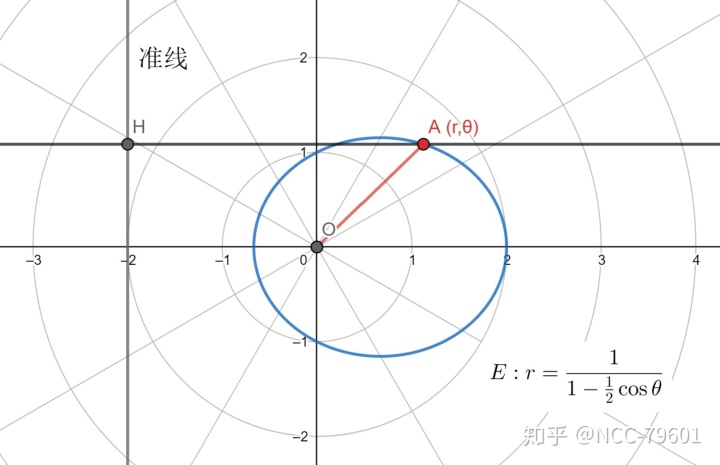
如图，设椭圆

又由圆锥曲线第二定义可知：

若右焦点在极点，则推导时用右准线即可。

应用

1) 极坐标下的焦半径公式

焦半径即极坐标方程中的

更新：有朋友在评论区问

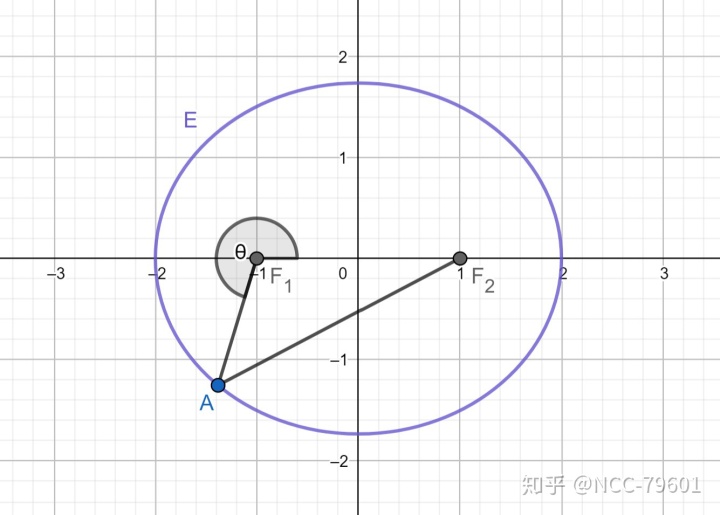
注意，这里

方向相同时转过的最小正角（类似辐角），而非 倾斜角，原因是在上图这种刁钻情况下， 倾斜角代替极角，那么公式中的那个正负号就需要 反号。对于双曲线，由于双曲线 有两支，因此对于左焦点

2) 倾斜角表示焦点弦长

拿左焦点弦为例，设左焦点弦所在直线倾斜角为

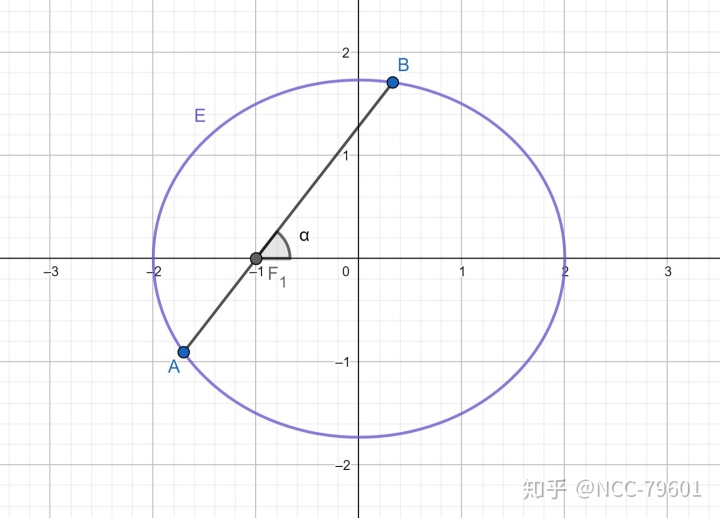
由于

双曲线的焦点弦比较复杂：

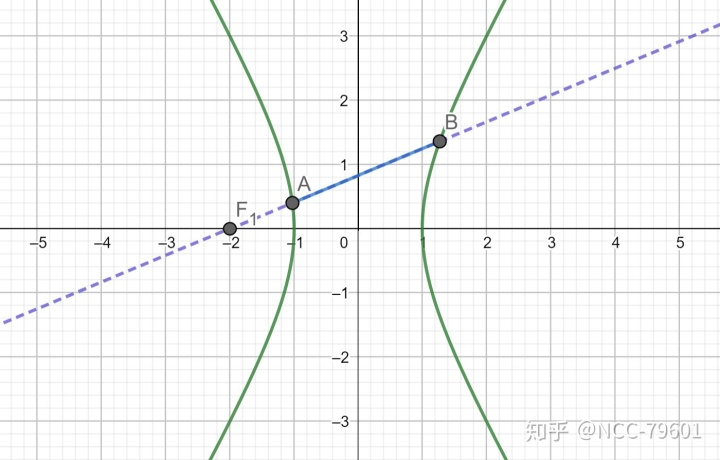
上图便出现了

抛物线中，由于离心率

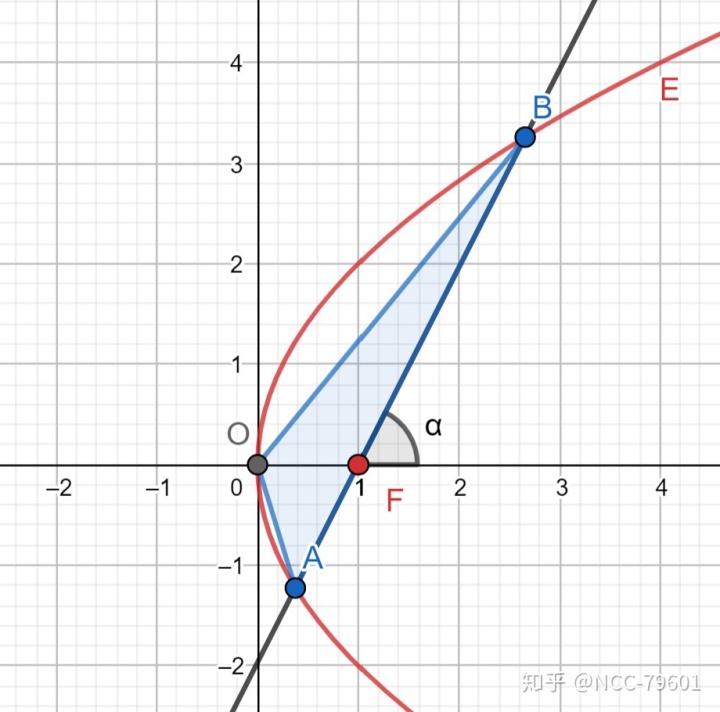
运用极坐标下的抛物线焦点弦长公式，如图所示的

而

中心在极点时的极坐标方程

不过有些时候，把焦点放在极点仍然不太方便，就可以直接把中心（直角坐标系中的原点）放在极点。

推导

设椭圆

整理可得：

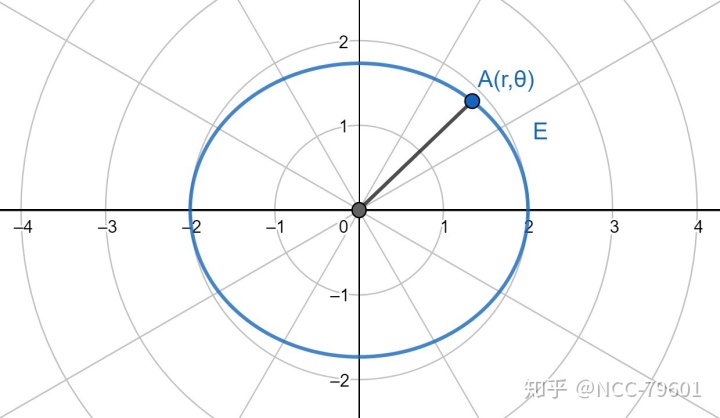
如果用

这两个方程表示的是同一个椭圆。双曲线与椭圆类似。

而对于抛物线，由于其方程为

应用

你应该还记得这道题：

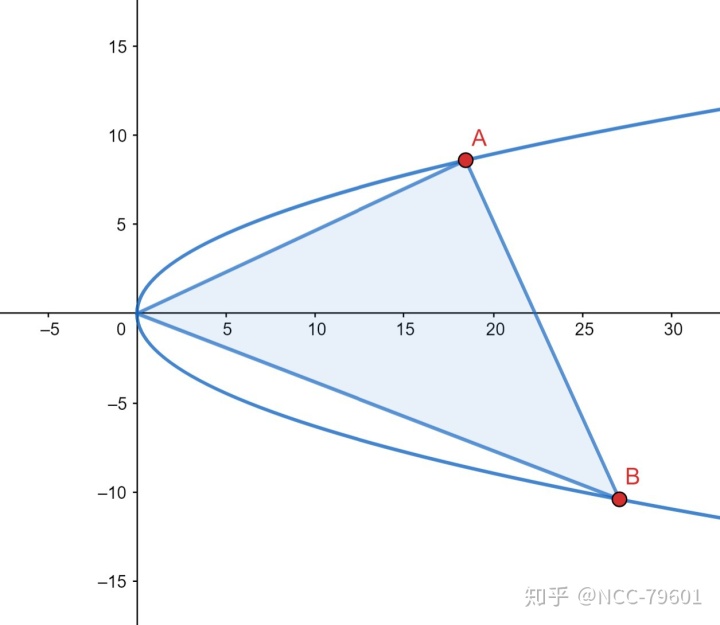
抛物线

当时你是怎么做的呢？我反正是设

这实在有些麻烦，不仅要暴解两个点的坐标，还要构造一个全等，证明过程书写量极大。而如果我们使用中心在极点的抛物线极坐标方程来证明这道题，事情会简单得多：

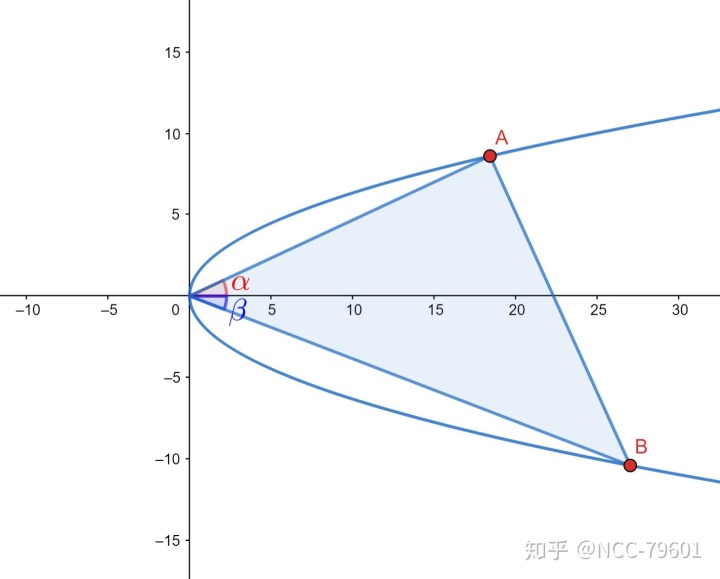
设

由抛物线方程

利用三角恒等变换化简上述等式，可得：

我现在需要证明

所以得证。

有没有感觉计算量、书写量都少了许多呢？

---

向量叉乘（外积）

叉乘是一种巧算三角形面积

平行四边形面积的好方法。它本是一种复杂的运算法则，其结果为垂直于原平面的一个新向量，物理的电磁学中很多东西（洛伦兹力等）都跟它有关；然而作为一个普通的高中生，我们只需要熟悉它作为面积计算工具的功能即可。如果已知

运算规则

设两向量

平行四边形面积为：

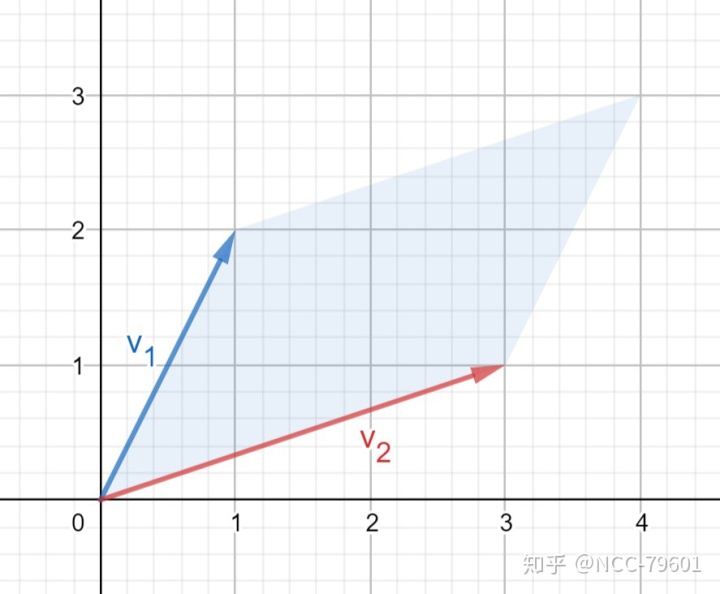
证明

此处只给出暴力证法。

设

也就是说，平面中的叉乘公式为：

注意上式中的两个

向量的模，右边表示 绝对值。

计算三角形面积

很容易想到，把上面的

应用

假设有一道圆锥曲线大题，你通过暴算的方法获知了三个点的坐标，现在需要求出三点围成的三角形面积的最值。传统方法是设出直线，利用各种距离公式暴算。但有了叉乘这个工具之后，只需要用两点坐标相减的方法随便求出两个向量，然后直接叉乘即可算出表达式。由于这两种方法本质相同（叉乘仅仅是简化了中间运算过程），因此得到的表达式一定是一致的，这也就意味着叉乘过程中将会出现大量的约分、抵消，为运算带来愉悦感。

此种方法甚至适用于计算这种异形四边形的面积：

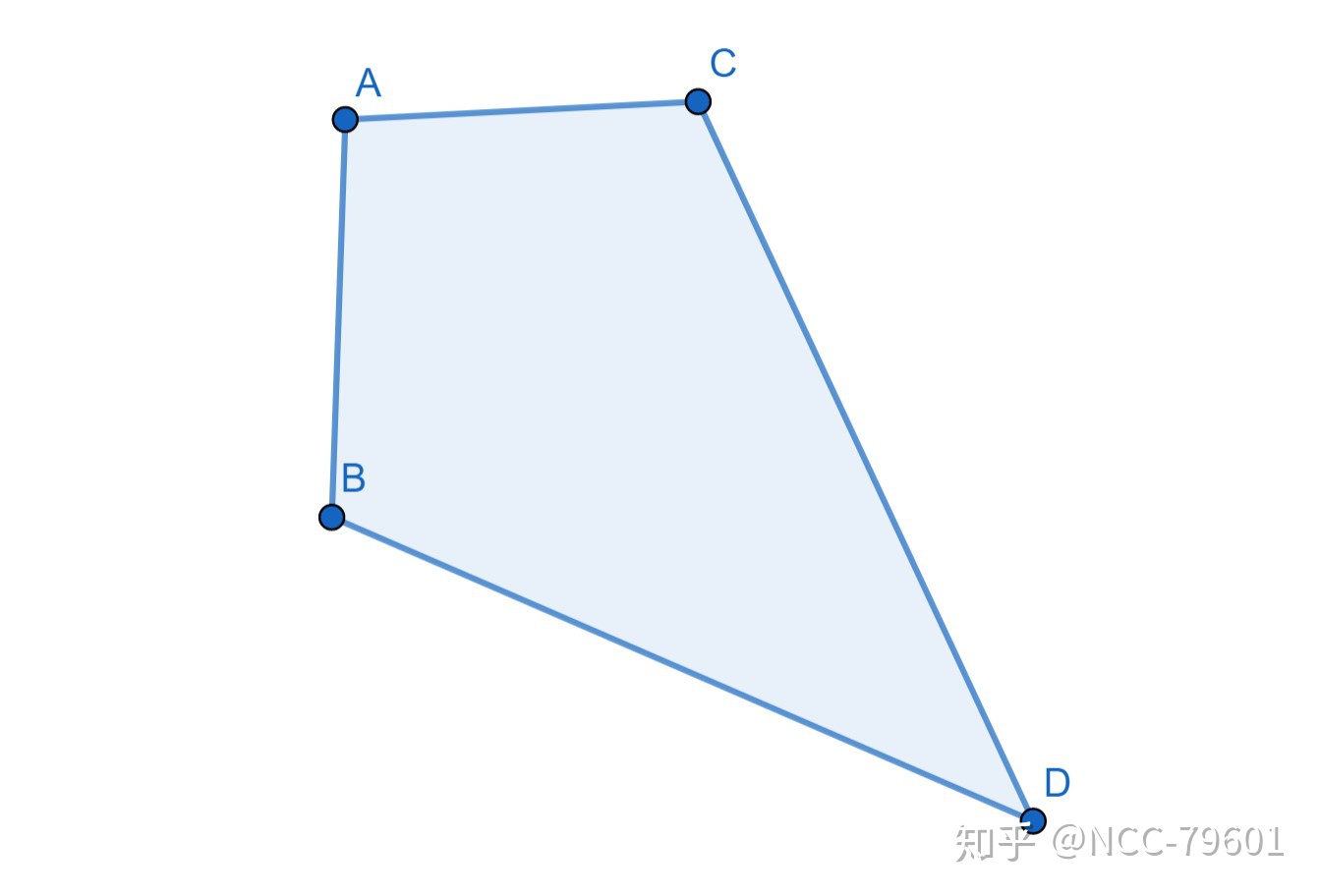
传统方法是切割为两个三角形，分别计算后相加。这种方法虽然容易想到，但其计算量与书写量非常大。如果使用叉乘工具，可以这样进行计算：

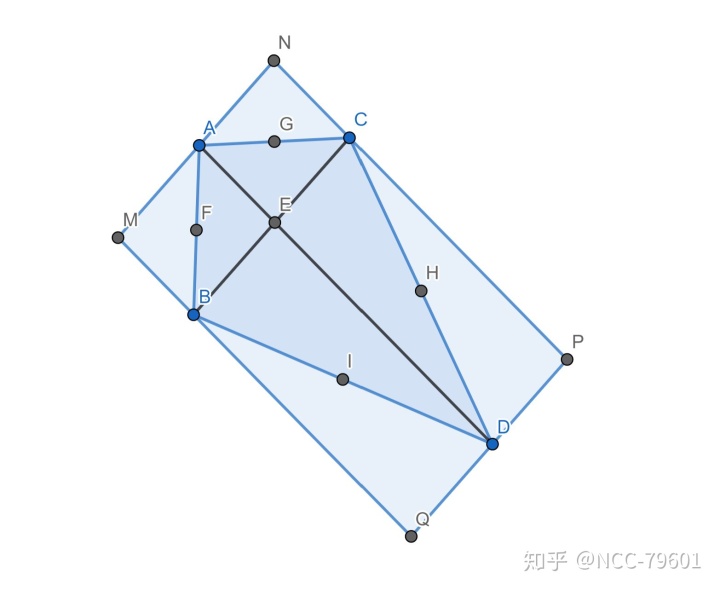
首先将多边形补全为一个平行四边形，为使用叉乘作准备。

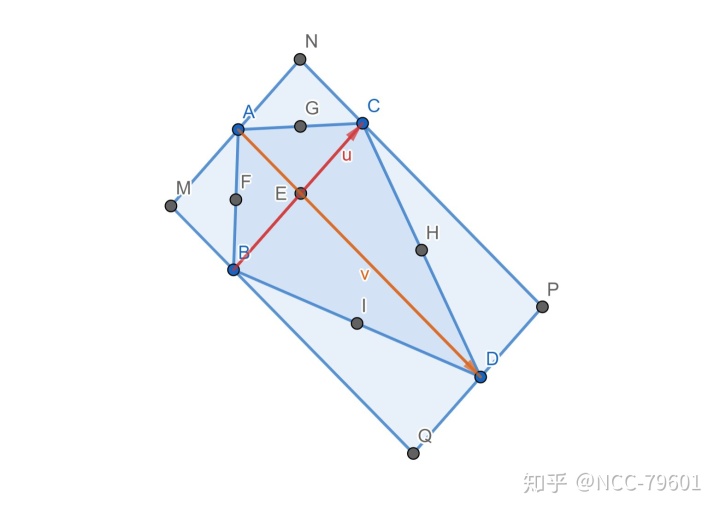
现在需要考虑的是如何计算出

然后取

这样就可以简便地算出

上面所述的方法仅在最后一步中有较大的字母运算量。不过正如上文提到的，叉乘仅仅简化了运算过程，最后的这部分运算是获得答案的必经之路，没有哪个方法能够将这个过程简化掉。所以，叉乘的计算量会比一般的方法少很多（关键是更好写，更装逼），除非你把向量的坐标算错了。

（更新）参数方程下的转换工具

实际上，叉乘还可以作为把表达式转化为三角函数的工具。比如下面这个例子：

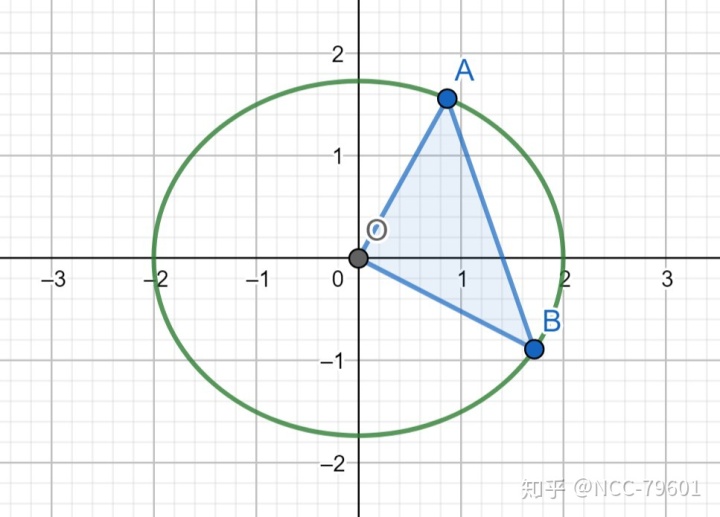
我们可以设

然后呢？似乎无法继续了。

实际上，我们可以使用椭圆的一种参数方程，把这道题转换为简单的三角函数求最值问题。参数方程如下：

所以重新设

非常明显有：

这也可以算作一个小结论。

---

优雅的暴力：暴解方程

如果你发现你需要解一个高次方程，并且你确定自己的方程是正确的，那么就可以用暴力的方法，获得方程的有理解（除非万不得已，不推荐主动使用）。

有理根定理

对于一个多项式函数

正负因数）。

证明

涉及到部分数论知识。我之前学过信竞，所以对此略有了解。若阅读起来有困难，就跳过证明，直接当结论记吧；反正这个定理还是比较简单的。

设最简分数

两边同时乘以

等式两边同时对

由于题设

应用

最简单的应用当然是快速解高次方程。如果你赌它的解为有理数，那么就可以列出最高次项、常数项的所有因数，然后获得所有可能的根，一个个地试。由于可能存在多个有理解，所以建议把所有可能的根都试一遍。

例如：对于

当然，既然知道了根，那就可以顺便把

不过，如果方程的解不幸地都是无理数，那么这个方法就没有用武之地了（只能脑解），直接猜

---

极点极线

注意：极点极线在大题中不能使用（高中教材中没有相关内容）！毕竟没有多少老师知道这玩意儿，所以写在试卷上几乎不可能得到过程分。不过有一种投机取巧的方法，那就是我的同学们津津乐道的四川话：

麻证麻解，把改卷老师麻到起！

不错，你可以列好所有方程，令

直接写出来的！这样就不会出现任何会引起改卷老师怀疑的地方，毕竟没有人会管你的计算过程；因此所有分数都到手了（笑）。

概念

极点极线是一种圆锥曲线（也适用于圆，因为圆是特殊的圆锥曲线）中的概念，它本质上是平面上点与直线之间的一种双映射：也就是说，关于同一个圆锥曲线，一个点唯一对应一条直线，一条直线也唯一对应一个点。

计算法则

设圆锥曲线

通俗一点，对于圆锥曲线的一般方程（注意，必须完全展开才能使用结论）

• 换为
  ；
• 换为
  ；
• 换为
  ；
• 常数项不变。

获知极线方程以后，也可以利用圆锥曲线方程反算出极点坐标，毕竟极点极线是一种双映射。

至于极点极线相关性质的证明，作为高中生（而非数竞选手）不需要过多深入研究。

几何意义

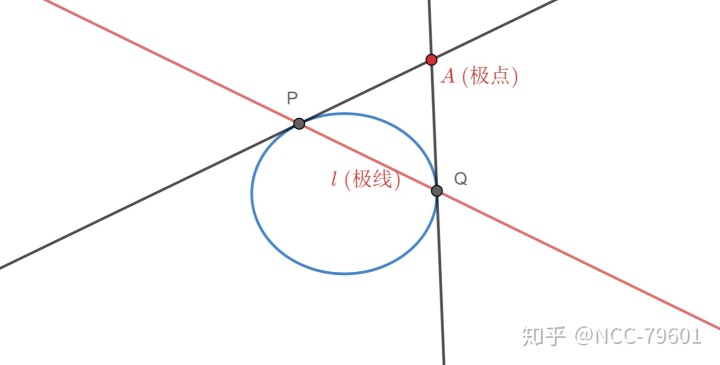
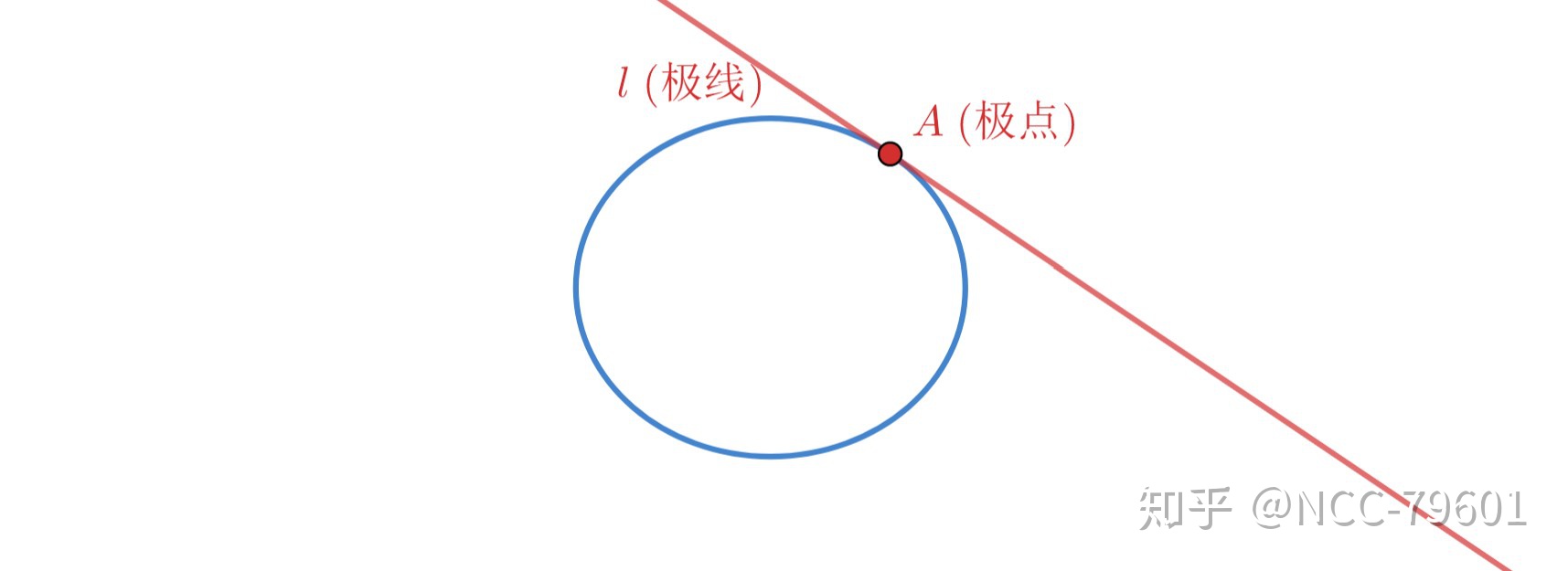
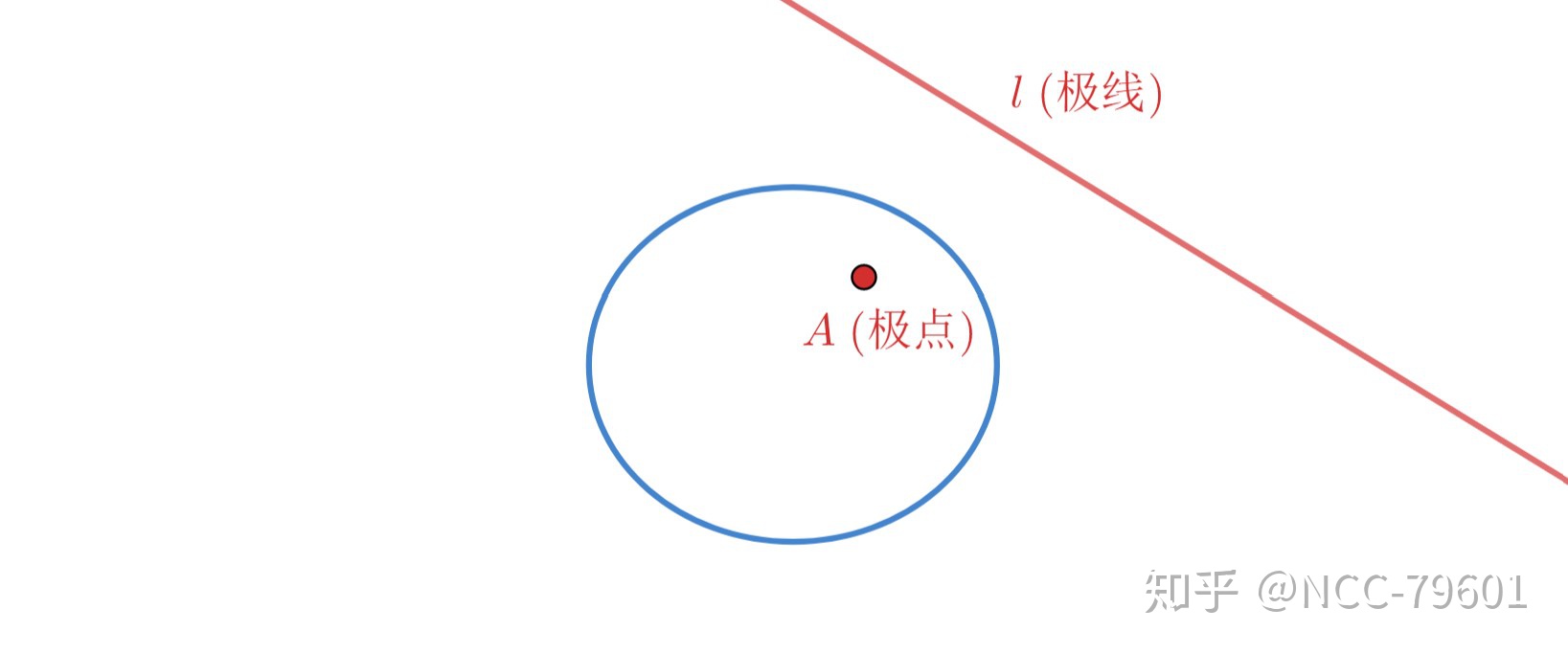
由上面三幅图可以很清晰地看出，极点

1. 点在圆锥曲线
   外，则
   为
   点的
   切点弦方程；
2. 点在圆锥曲线
   上，则
   为
   点处的
   切线方程；
3. 点在圆锥曲线
   内，则
   为与圆锥曲线
   相离的一条直线（虚切点弦方程）。

一个不太严谨的推导（隐函数求导）

我偷个懒…就用最简单的椭圆

首先，

①如果点

式子中的

所以

即

②如果点

我们又知道

对这个两个式子，我们可以反着理解：除了说这是“

所以

当你写切线方程或者切点弦方程的时候，就可以用这种方式秒杀。

几何意义

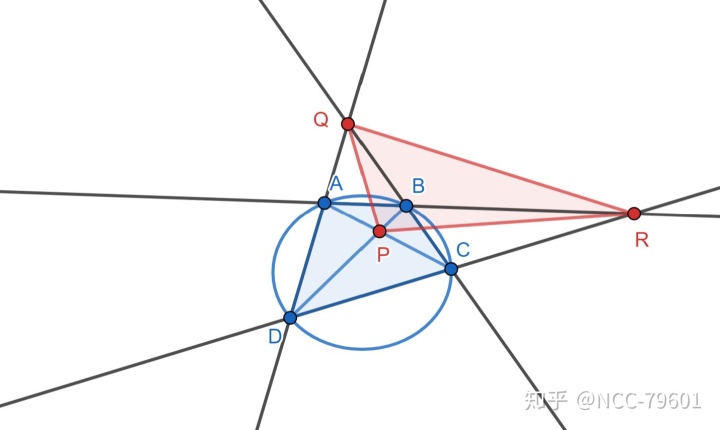
上图中，

任意一个顶点的对边就是它关于圆锥曲线的极线。这个三角形叫做 自极三点形。

这个性质实际上除了美妙并没有太大的用处，但是在原图基础上再作一些线，就会出现极点极线的另一个几何性质：

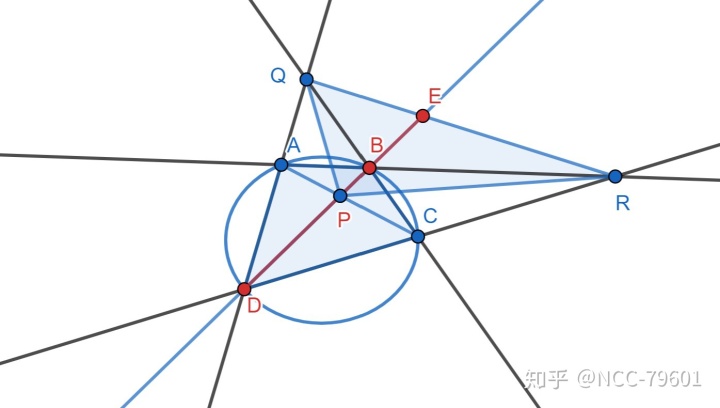
延长

或者调换一下顺序：

这四个点叫做调和点列。有一堆专有名词来描述它们的位置关系，这里我们只需要记住

如何记住这个比值关系呢？我有比较精炼的一句话：两点到另两点的距离之比相等。

“调和共轭”这个概念已经略微接触高等几何了，不建议深究证明。

应用

1) 巧算切线

切点弦方程

上文已经提到过，为了保证不被扣过程分，建议还是写上直线与圆锥曲线联立方程，然后令

更新：除了这种方法外，也可以使用我在推导过程中用到的隐函数求导来写切线

2) 处理复杂几何关系

调和共轭的比值式有多种变形，最常见的是取一个中点，然后告诉你一条线段长度的平方等于另外两条线段长度之积。这种时候要进行倍长处理，然后对等式瞎代换一通；或者利用等比性质，把等式转化为熟悉的比值式。这些以调和共轭作为背景的题目，一般都是几何翻译难度较高、计算量极大，所以还是可以采用麻解的方法。

总而言之，一旦你知道了这些题目的背景，它那些看似唬人的条件对于你来说只是个花架子罢了；要不是因为过程分的束缚，你是可以秒杀它的。

---

更新：LZ马上高三，已经学完导数了，相关的内容也更新了。现在才发现这些花里胡哨的东西的用处并不是很大，韦达定理+暴力真香（汗）。

需要强调的是，上面这些高级方法的意义只能是“锦上添花”。如果你还不能熟练使用韦达定理简化运算，还不知道如何巧设参变量、函数如何求最值，那么即使学了我所讲的这些技巧也不会对提分有任何帮助。毕竟，这些所谓高级方法能够解的题目，韦达定理 + 暴算是绝对能解的，只是前者思维难度更大，后者计算量更大。因此，基本功是最重要的，不刷够题目就不要来学这些旁门左道。

希望这篇文章对你有所帮助，有所启发。