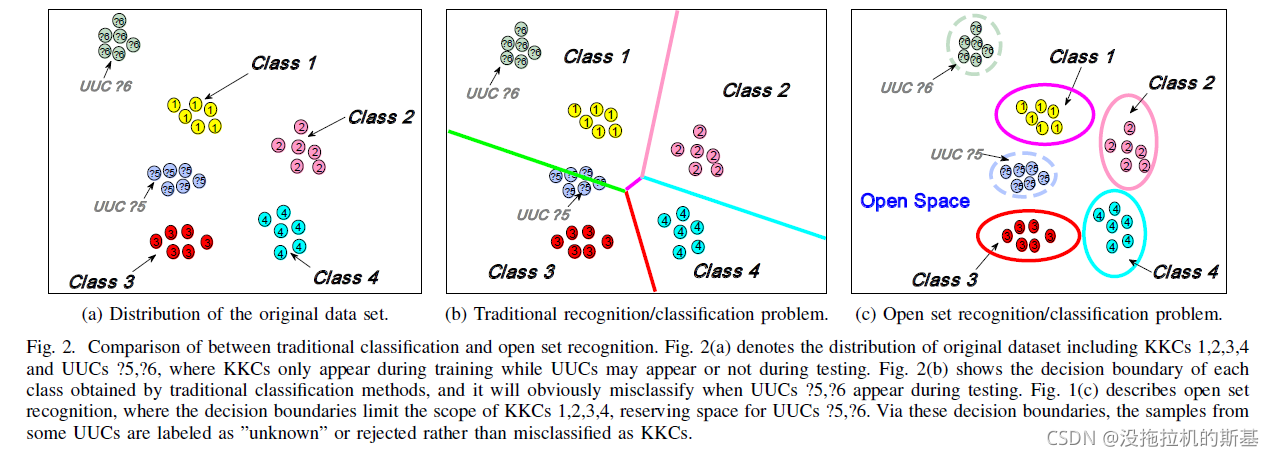
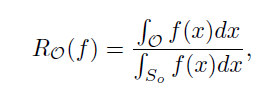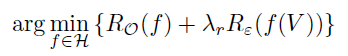开集识别
闭集识别
训练集中的类别和测试集中的类别是一致的,最常见的就是使用公开数据集进行训练,所有数据集中的图像的类别都是已知的,没有未知种类的图像。传统的机器学习的算法在这些任务上已经取得了比较好的效果。
开集识别简述
现实场景中更多的是开放和非静态的环境,比如,一些没有见过的情况会意外出现。针对这一挑战提出的方法有持续学习、迁移学习、域适应、零样本、少样本学习、开集识别和分类等。
开集识别简单定义是,一个在训练集上训练好的模型,当利用一个测试集(该测试集的中包含训练集中没有的类别)进行测试时,如果输入已知类别数据,输出具体的类别,如果输入的是未知类别的数据,则进行合适的处理(识别为unknown)。
示例 : 猫狗识别模型,输入一张荷花或者大象的图像,模型可能会告诉你80% 的概率为 猫。
想要的结果 : 输入不为猫狗的图像,模型输出为未知类别,输入猫狗图像,模型输出对应具体的类别
数据集类别划分
-
KKCs known known classes
具有明确标签的正训练样本(对其他KKCs为负样本),包含相应的伴随信息(语义和属性信息等)的类别
-
KUCs known unknown classes
被标记为负样本,不必要被划分为一个具体的类别,比如background class,universum class(对于一个具体问题不属于任何类别的样本)
-
UKCs unknown known classes
训练时没有可用的样本,但是有可用的伴随信息(语义和属性信息等)
-
UUCs unknown unknown classes
训练时没有可用样本,也没有伴随信息(语义和属性信息等)
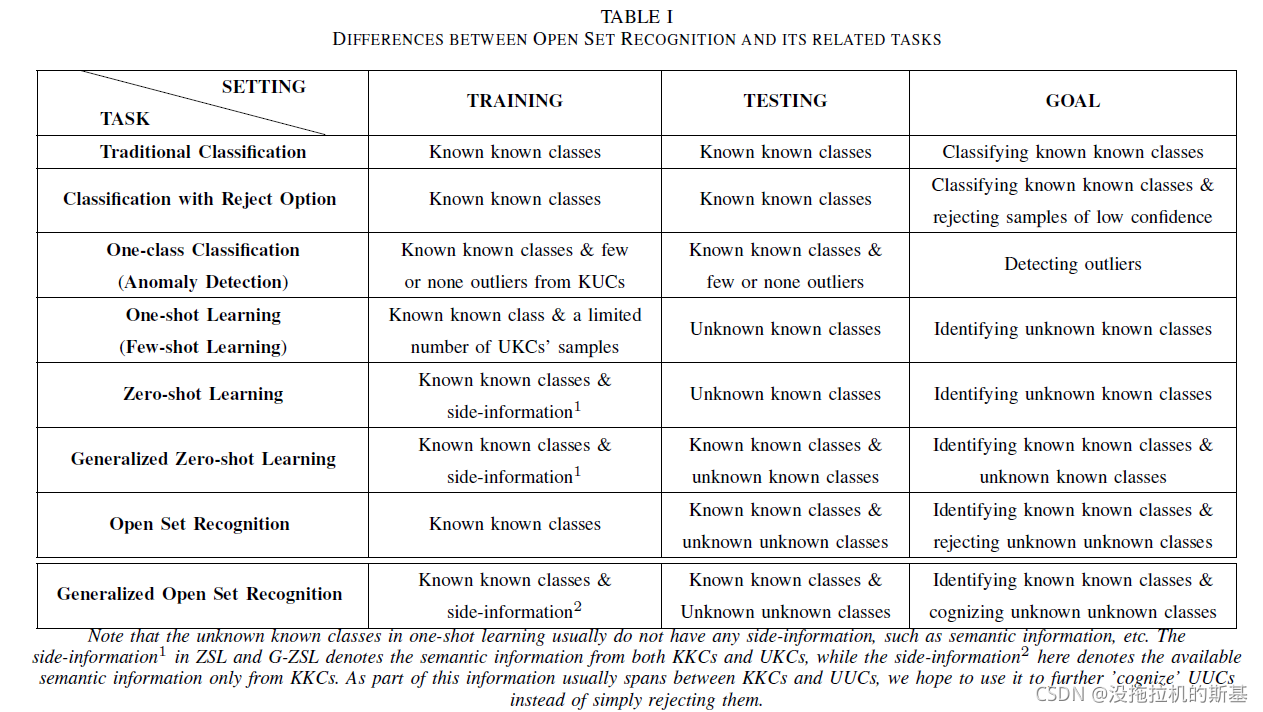
传统分类只考虑KKCs;zero-shot learning(ZSL) 关注识别UKCs;one/few-shot看作是ZSL的扩展,训练时有有限数量的UKCs;开集识别(OSR)训练时只有KKCs,测试时有UUCs,需要准确分类KKCs同时需要正确的策略拒绝UUCs。
下表描述了开集识别和相关任务的区别:
相关定义
- 开放空间风险
远离已知数据的空间(包括KKCs和KUCs)通常被认为是开放空间 O,因此将该空间中的任何样本任意标注为KKC必然会带来风险,这被称为开放空间风险(open space risk):
R
O
R_O
RO 。由于UUCs在训练中是不可知的,因此通常很难对开放空间风险进行定量分析。另外,给出了
R
O
R_O
RO 的定性描述,其中它被形式化为开放空间 O 相对于整体测度空间 的相对测度,计算如下:
式中,f 为可测识别函数。f(x) = 1表示KKCs中的某些类被识别,否则 f(x) = 0。在这种形式化下,开放空间中越多的样本被标记为KKCs,
R
O
R_O
RO 越大。
- 开放集识别问题
设 V 为训练数据,设
R
O
R_O
RO 、
R
ε
R_{\varepsilon}
Rε 分别为开放空间风险和经验风险(对训练集中的所有样本点损失函数的平均最小化,经验风险越小说明模型f(x)对训练集的拟合程度越好)。那么开放集识别的目标就是找到一个可测量的识别函数:f ∈H,其中f(x) > 0表示识别正确,f 是通过最小化以下Open Set Risk来定义的:
Open Set Risk 在允许识别函数的空间上平衡了经验风险和开放空间风险。
开集识别的解决方案
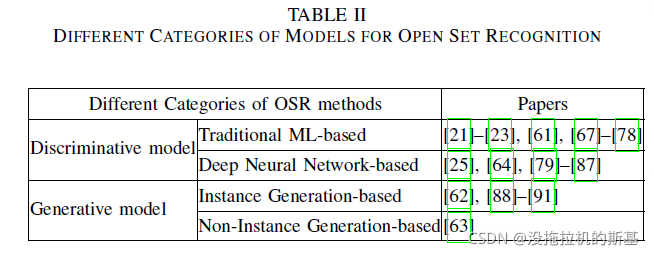
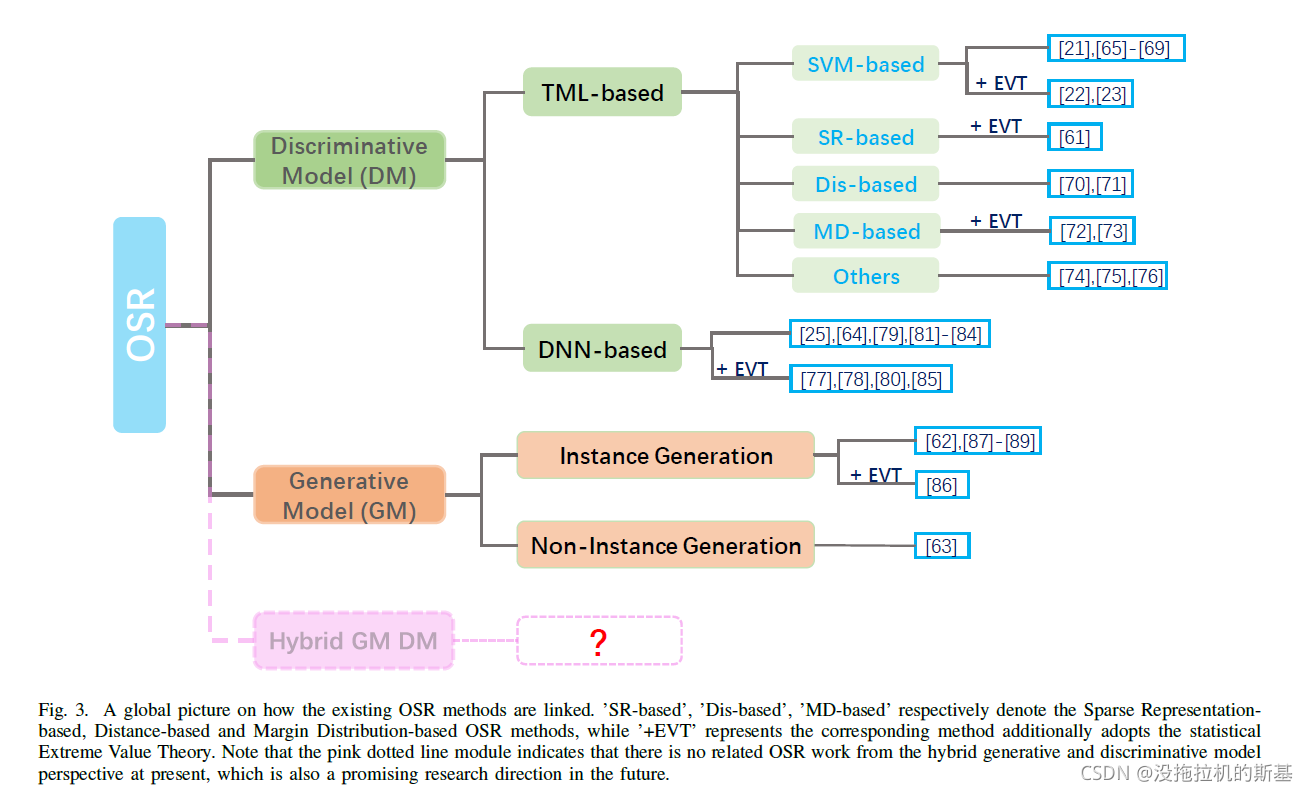
可以通过判别模型和生成模型的角度将开集识别的模型进行分类【判别模型和生成模型的区别】
OpenMax
Towards Open Set Deep Networks
Softmax是深度学习分类网络中最常见的最后一层的激活函数,用于概率值的生成。**这不可避免地会带来归一化问题,使其固有的封闭集特性。**例如,在处理UUCs的样本时,DNNs常常做出错误的预测,甚至过于自信。所以《Towards Open Set Deep Networks》提出了openmax层来替代softmax,作为开放集深度网络的第一个解决方案。
算法流程:
只计算并保留所有预测样本正确样本(预测错误的输出舍弃)的特征值(特征值的长度就是类别的长度,比如最后的类别数量为3,那么整个特征就是长度为3的向量,而不是之前一层的向量)。
求出所有预测正确样本的向量,根据不同的类别将这些向量对应分开,然后分别计算每个类别对应向量的均值作为该类别的中心。
分别计算每个类别中每个样本对应向量和其类别中心的距离,然后对这些距离进行排序,针对排序后的几个尾部极大值进行极大值理论分析,这些极大值的分布符合weibull分布,所以使用weibull分布(libmr中的fithigh方法)来拟合这些极大的距离,得到一个拟合分布的模型。
当来了一个新的测试图像的时候,这时候输入模型,先得到对应的dense向量(softmax的前一层),然后针对该向量分别针对每个类别计算与其之间的距离(共得到N个距离),然后针对上述得到的每个距离分别使用每个类别对应的拟合模型对其进行预测,最后会分别得到一个分数FitScores,这个分数就是指该测试图像特征值归属于其对应类别的概率,所以一共是有N个分类的。然后根据该图像的最终输出(此处为softmax的输出),根据该概率分数的输出继进行排序,然后计算w的值(该值的计算就是根据采用tail的个数(即阿尔法的值)来计算的)
f
o
r
i
=
1...
α
w
=
1
−
F
i
t
S
c
o
r
e
s
∗
(
α
−
i
)
/
α
for \quad i = 1...\alpha \quad w = 1-FitScores*(\alpha-i)/\alpha
fori=1...αw=1−FitScores∗(α−i)/α
然后将该向量分别针对每个类别计算与其之间的距离与上述得到的W进行相乘,后续再进行类似softmax的操作,最终得到两个分数,一个是openmax后的分数,一个是unknown的分数,注意这里得到的openmax的类别比softmax输出的类别多一个类别,也就是unknown的类别。
极值理论(EVT):
每过一段时间,小概率时间就会发生,比如巨大的台风,或者跳高记录被打破。但是到底这样的事件有多极端?极值理论可以回答这个问题。利用以往的记录,比如说500年来的洪水记录,极值理论就可以预测将来发生更大洪水的可能性。
极值理论关注风险损失分布的尾部特征,通常用来分析概率罕见的事件,它可以依靠少量样本数据,在总体分布未知的情况下,得到总体分布中极值的变化情况,具有超越样本数据的估计能力。
韦伯分布(可靠性分析):