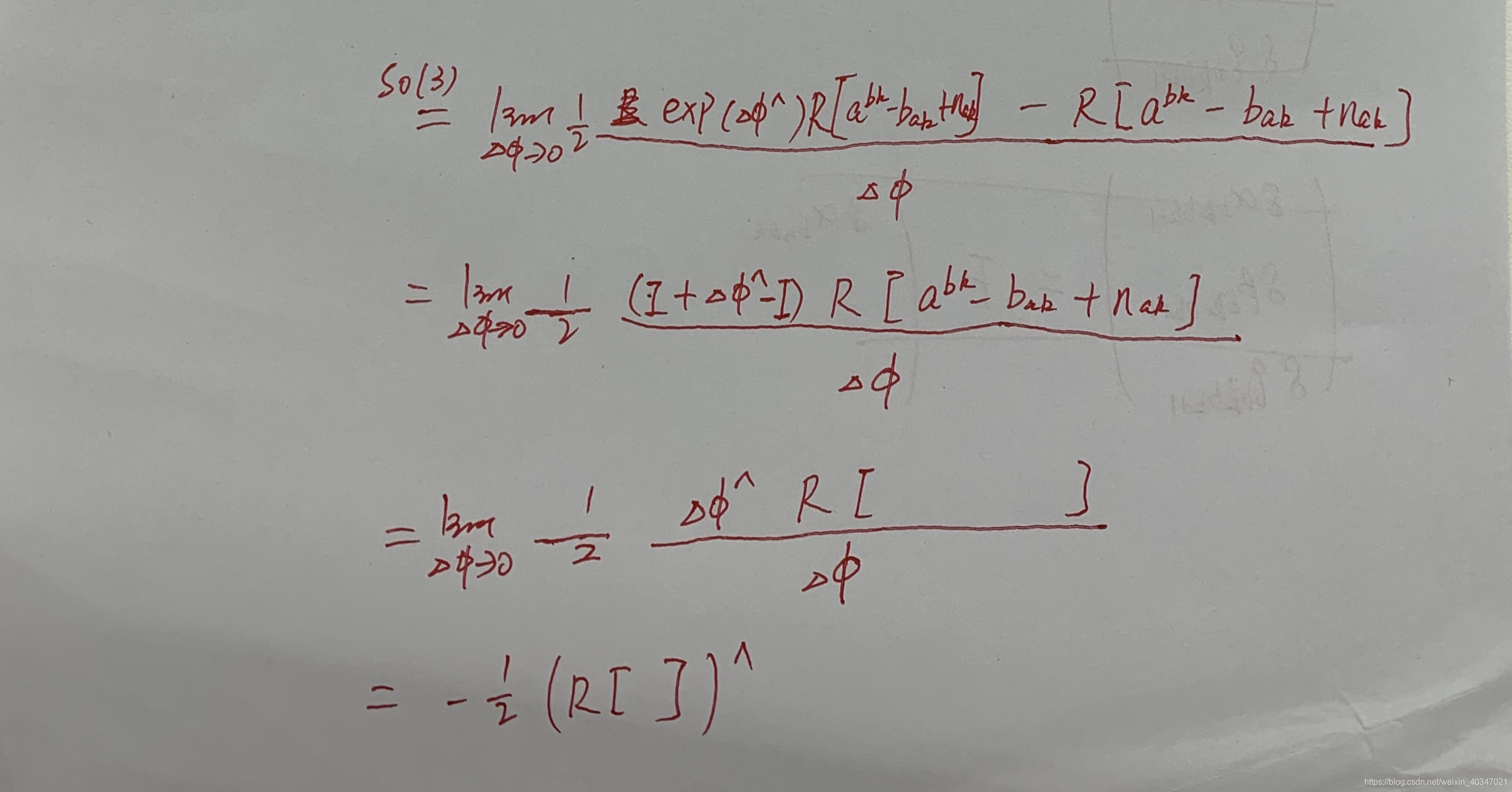视觉slam vins 双目 第一讲 IMU预积分及其残差
视觉slam入门者,欢迎大佬指正错误
主要以vins为切入点分析vio(视觉惯性耦合系统)
第一讲主要分系imu。
1. imu预积分
预积分就是为了简便计算,对每两帧图像之间的imu数据进行积分(vins中采用中值积分),并且以这两帧图像之间的第一帧imu数据为标准系进行积分:
2. 预积分离散化
3. 预积分的误差传递以及协防差矩阵
4. IMU残差(放入ceres求解)
vins中对应的代码及其注释
// An highlighted block
#pragma once
#include "../utility/utility.h"
#include "../estimator/parameters.h"
#include <ceres/ceres.h>
using namespace Eigen;
class IntegrationBase
{
public:
IntegrationBase() = delete;
IntegrationBase(const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
: acc_0{_acc_0}, gyr_0{_gyr_0}, linearized_acc{_acc_0}, linearized_gyr{_gyr_0},
linearized_ba{_linearized_ba}, linearized_bg{_linearized_bg},
jacobian{Eigen::Matrix<double, 15, 15>::Identity()}, covariance{Eigen::Matrix<double, 15, 15>::Zero()},
sum_dt{0.0}, delta_p{Eigen::Vector3d::Zero()}, delta_q{Eigen::Quaterniond::Identity()}, delta_v{Eigen::Vector3d::Zero()}
{
// 噪声矩阵
// ACC_N, GYR_N: 加速度计和陀螺白噪声均值
// ACC_W, GYR_W: 加速度计和陀螺随机游走
noise = Eigen::Matrix<double, 18, 18>::Zero();
noise.block<3, 3>(0, 0) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity(); // k时刻三轴加速度噪声
noise.block<3, 3>(3, 3) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity(); // k时刻三轴角速度噪声
noise.block<3, 3>(6, 6) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity(); // k+1时刻三轴加速度噪声
noise.block<3, 3>(9, 9) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity(); // k+1时刻三轴角速度噪声
noise.block<3, 3>(12, 12) = (ACC_W * ACC_W) * Eigen::Matrix3d::Identity(); // k时刻加速度偏置噪声
noise.block<3, 3>(15, 15) = (GYR_W * GYR_W) * Eigen::Matrix3d::Identity(); // k时刻角速度偏置噪声
}
void push_back(double dt, const Eigen::Vector3d &acc, const Eigen::Vector3d &gyr)
{
dt_buf.push_back(dt);
acc_buf.push_back(acc);
gyr_buf.push_back(gyr);
propagate(dt, acc, gyr);
}
//状态重传播函数(reprogate)
//该函数在后端完成优化,给出加速度计和陀螺仪零偏新的最优估计值后,基于新的估计值对已有的IMU预积分进行重递推,
//函数入口参数为优化后的零偏值_linearized_ba和_linearized_bg。
void repropagate(const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
{
sum_dt = 0.0;
acc_0 = linearized_acc;
gyr_0 = linearized_gyr;
delta_p.setZero();
delta_q.setIdentity();
delta_v.setZero();
linearized_ba = _linearized_ba;
linearized_bg = _linearized_bg;
jacobian.setIdentity();
covariance.setZero();
for (int i = 0; i < static_cast<int>(dt_buf.size()); i++)
propagate(dt_buf[i], acc_buf[i], gyr_buf[i]);
}
void midPointIntegration(double _dt,
const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1,
const Eigen::Vector3d &delta_p, const Eigen::Quaterniond &delta_q, const Eigen::Vector3d &delta_v,
const Eigen::Vector3d &linearized_ba, const Eigen::Vector3d &linearized_bg,
Eigen::Vector3d &result_delta_p, Eigen::Quaterniond &result_delta_q, Eigen::Vector3d &result_delta_v,
Eigen::Vector3d &result_linearized_ba, Eigen::Vector3d &result_linearized_bg, bool update_jacobian)
{
//ROS_INFO("midpoint integration");
//和论文中推导采用欧拉积分法不同,代码中实际采用的是中值积分法,且认为在整个[k,k+1][k,k+1]过程中,加速度计和陀螺仪零偏保持不变。
Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);
Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);
Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt;
result_delta_v = delta_v + un_acc * _dt;
result_linearized_ba = linearized_ba;
result_linearized_bg = linearized_bg;
if(update_jacobian) // update_jacobian = 1
{
Vector3d w_x = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
Vector3d a_0_x = _acc_0 - linearized_ba;
Vector3d a_1_x = _acc_1 - linearized_ba;
Matrix3d R_w_x, R_a_0_x, R_a_1_x;
R_w_x<<0, -w_x(2), w_x(1),
w_x(2), 0, -w_x(0),
-w_x(1), w_x(0), 0;
R_a_0_x<<0, -a_0_x(2), a_0_x(1),
a_0_x(2), 0, -a_0_x(0),
-a_0_x(1), a_0_x(0), 0;
R_a_1_x<<0, -a_1_x(2), a_1_x(1),
a_1_x(2), 0, -a_1_x(0),
-a_1_x(1), a_1_x(0), 0;
MatrixXd F = MatrixXd::Zero(15, 15);
F.block<3, 3>(0, 0) = Matrix3d::Identity();
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt +
-0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt;
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt;
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt;
F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt +
-0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
F.block<3, 3>(6, 6) = Matrix3d::Identity();
F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
F.block<3, 3>(9, 9) = Matrix3d::Identity();
F.block<3, 3>(12, 12) = Matrix3d::Identity();
//cout<<"A"<<endl<<A<<endl;
MatrixXd V = MatrixXd::Zero(15,18);
V.block<3, 3>(0, 0) = 0.25 * delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 3) = 0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * 0.5 * _dt;
V.block<3, 3>(0, 6) = 0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 9) = V.block<3, 3>(0, 3);
V.block<3, 3>(3, 3) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(3, 9) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(6, 0) = 0.5 * delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 3) = 0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * 0.5 * _dt;
V.block<3, 3>(6, 6) = 0.5 * result_delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 9) = V.block<3, 3>(6, 3);
V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;
//step_jacobian = F;
//step_V = V;
// 预积分更新的雅克比,主要是用对于bias的雅克比,来更新预积分值
// 求得是对于i时刻的jacobi矩阵,,,而F代表的雅克比是对上一帧imu数据的雅克比
jacobian = F * jacobian; //jacobian的初始化为单位阵I
//预积分误差的协方差的传递
covariance = F * covariance * F.transpose() + V * noise * V.transpose();
}
}
void propagate(double _dt, const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1)
{
dt = _dt;
acc_1 = _acc_1;
gyr_1 = _gyr_1;
Vector3d result_delta_p;
Quaterniond result_delta_q;
Vector3d result_delta_v;
Vector3d result_linearized_ba;
Vector3d result_linearized_bg;
// 预积分量的中值积分
midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1, delta_p, delta_q, delta_v,
linearized_ba, linearized_bg,
result_delta_p, result_delta_q, result_delta_v,
result_linearized_ba, result_linearized_bg, 1);
//checkJacobian(_dt, acc_0, gyr_0, acc_1, gyr_1, delta_p, delta_q, delta_v,
// linearized_ba, linearized_bg);
//赋值成上一时刻的误差
delta_p = result_delta_p;
delta_q = result_delta_q;
delta_v = result_delta_v;
linearized_ba = result_linearized_ba;
linearized_bg = result_linearized_bg;
delta_q.normalize();
sum_dt += dt;
//赋值成上一时刻
acc_0 = acc_1;
gyr_0 = gyr_1;
}
/*****************************************************************************
* 残差评估函数(evaluate)
* 该函数用于在后端非线性优化中每一次优化后评估IMU预积分的残差,函数入口参数分别为:
* 优化后的第k帧预积分状态变Pi、Qi、Vi、Bai、Bgi
* 优化后的第k+1帧预积分状态量Pj、Qj、Vj、Baj、Bgj
* 函数返回值为k和k+1之间IMU预积分状态与非线性优化状态之间的残差,用于构建后端的非线性优化误差函数
* (理想状态下残差应该为零,实际情况下残差应该逐渐收敛于一个小值附近)。
* ————————————————
*********************************************************************************/
// 注意是优化之后的残差!!!!!!!!!!!!!!!!!!!!!
Eigen::Matrix<double, 15, 1> evaluate(const Eigen::Vector3d &Pi, const Eigen::Quaterniond &Qi, const Eigen::Vector3d &Vi, const Eigen::Vector3d &Bai, const Eigen::Vector3d &Bgi,
const Eigen::Vector3d &Pj, const Eigen::Quaterniond &Qj, const Eigen::Vector3d &Vj, const Eigen::Vector3d &Baj, const Eigen::Vector3d &Bgj)
{
Eigen::Matrix<double, 15, 1> residuals;
/****************************
* O_P = 0,
* O_R = 3,
* O_V = 6,
* O_BA = 9,
* O_BG = 12
****************************/
Eigen::Matrix3d dp_dba = jacobian.block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = jacobian.block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dq_dbg = jacobian.block<3, 3>(O_R, O_BG);
Eigen::Matrix3d dv_dba = jacobian.block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = jacobian.block<3, 3>(O_V, O_BG);
// Bai是优化之后的i时刻的偏置 linearized_ba是定值 Bai Baj 是需要优化的值
Eigen::Vector3d dba = Bai - linearized_ba;
Eigen::Vector3d dbg = Bgi - linearized_bg;
// 下面代表预计分的值 在i时刻附近的bias附近使用一阶泰勒展开来近似
// 当bias估计轻微改变时,我们可以使用如下的一阶近似 对中值积分得到的预积分测量值进行矫正,
// 而不重传播,从而得到 更加精确的预积分测量值(bias修正的线性模型)
Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg);
Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg;
Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg;
// 计算优化残差
residuals.block<3, 1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt) - corrected_delta_p;
residuals.block<3, 1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
residuals.block<3, 1>(O_V, 0) = Qi.inverse() * (G * sum_dt + Vj - Vi) - corrected_delta_v;
residuals.block<3, 1>(O_BA, 0) = Baj - Bai;
residuals.block<3, 1>(O_BG, 0) = Bgj - Bgi;
return residuals;
}
double dt; // 每次预积分的时间周期长度 imu的帧间
Eigen::Vector3d acc_0, gyr_0; // t时刻对应的IMU测量值
Eigen::Vector3d acc_1, gyr_1; // t+1时刻对应的IMU测量值
const Eigen::Vector3d linearized_acc, linearized_gyr; // k帧图像时刻对应的IMU测量值(与图像对齐的IMU的测量值)
Eigen::Vector3d linearized_ba, linearized_bg; // 加速度计和陀螺仪零偏,在[k,k+1]图像关键帧区间上视为不变
Eigen::Matrix<double, 15, 15> jacobian, covariance; // 预积分误差的雅克比矩阵
Eigen::Matrix<double, 15, 15> step_jacobian;
Eigen::Matrix<double, 15, 18> step_V;
Eigen::Matrix<double, 18, 18> noise; //系统噪声矩阵
double sum_dt; //所有IMU预积分区间的总时长,由于量测的不同步性,不一定有sum_dt = (k+1)-k
Eigen::Vector3d delta_p; // 位置预积分
Eigen::Quaterniond delta_q; // 旋转四元数预积分
Eigen::Vector3d delta_v; // 速度预积分
std::vector<double> dt_buf; // 用于存储每次预积分时间dt的寄存器
std::vector<Eigen::Vector3d> acc_buf; // 用于存储每次预积分加速度量测的寄存器
std::vector<Eigen::Vector3d> gyr_buf; // 用于存储每次预积分角速度量测的寄存器
};