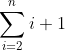第8章---排序

void InsertSort(ElemType a[], int n)
{
	int i, j;
	for (i = 2; i < n; i++) {//依次将a[2]~a[n]插入到前面已排序序列
		if (a[i] < a[i - 1]) {
			a[0] = a[i];//复制为哨兵
			for (j = i - 1; a[0] < a[j]; j--)
				a[j + 1] = a[j];//从后往前查找插入位置，并且向后挪位
		    a[j + 1] = a[0];	
        }
	}
}

空间效率：仅使用了常数个辅助单元，为O(1)。

时间效率：在排序过程中，向有序子表中逐个插入元素的操作进行了n-1趟，每趟操作都分为比较关键字和移动元素，而比较次数和移动次数取决于待排序表的初始状态。

在最好情况下，表中元素已有序，都只需要比较一次而不用移动元素，时间复杂度为O(1)。
在最坏情况下，表中元素顺序刚好与排序结果相反(逆序)，总的比较次数达到最大为 $\sum_{i=2}^{n}i+1$

所以平均情况下总的比较次数与总移动次数约为n^2/4。因此直接插入排序算法的时间复杂度为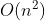 $O(n^{2})$ 。

稳定性：由于每次插入元素总是从后往前比较再移动，所以不会改变相对位置，即直接插入排序是一个稳定的排序方法。

适用性：顺序存储和链式存储结构均适用。

8.1.2 折半插入排序

void InsertSort2(ElemType a[], int n)
{
	int i, j;
	int low, high, mid;
	for (i = 2; i < n; i++) {
		a[0] = a[i];
		low = 1; high = i - 1;
		while (low < high) {
			mid = (low + high) / 2;
			if (a[mid] > a[0])
				high = mid - 1;
			else
				low = mid + 1;//若mid==a[0]为保证稳定性，继续向右查找
		}
		for (j = i - 1; j >= high + 1; --j)//插入到high之后
			a[j + 1] = a[j];
		a[high + 1] = a[0];
	}
}

当排序表为顺序表时，才可以使用折半插入排序。从上述算法中，元素的比较次数为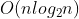 $O(nlog_{2}n)$ ，该比较次数仅取决于元素个数n；而移动次数并未改变。因此折半插入排序的时间复杂度仍是 $O(n^{2})$ 。

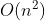
折半插入排序是一种稳定的排序。

8.1.3 希尔排序

直接插入排序的时间复杂度是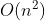 $O(n^{2})$ ，但若是待排序列是正序的，其时间复杂度可提升为 O(n) 。希尔排序正是基于这两点分析对直接插入排序进行改进而得来的，又称缩小增量排序。

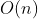
void ShellSort(ElemType a[], int n)
{
	int dk,i,j;
	for (dk = n / 2; dk >= 1; dk /= 2) {
		for (i = dk + 1; i <= n; ++i) {
			if (a[i] < a[i - dk]) {
				a[0] = a[i];	//此处a[0]仅作暂存作用
				for (j = i - dk; j > 0 && a[0] < a[j]; j -= dk)
					a[j + dk] = a[j];
				a[j + dk] = a[0];
			}
		}
	}
}

空间效率：仅使用了常数个辅助单元，空间复杂度为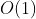 O(1) 。

时间效率：当n处于某个特定范围时，时间复杂度约为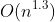 $O(n^{1.3})$ ，再最坏情况下时间复杂度为 $O(n^{2})$

希尔算法可能会改变记录的相对次序，因此是不稳定的算法；并且只适用于线性表为顺序存储结构的情况。

8.2 交换排序

所谓交换，是指根据序列中两个元素关键字的比较结果来兑换这两个记录在序列中的位置。

8.2.1 冒泡排序

冒泡排序的基本思想是：从后往前或者从前往后两两比较相邻元素的值，若为逆序(a[i-1]>a[i])，则交换他们。

每趟冒泡排序就是把序列中最小的元素放在序列的最终位置。

//冒泡算法
void swap(int a, int b)
{
	int temp;
	a = temp;
	a = b;
	b = temp;
}
void BubbleSort(ElemType a[], int n)
{
	int i, j;
	bool flag;
	for (i = 0; i < n; i++) {
		flag=false;//标记此趟是否发生了交换
		for (j = n - 1; j > n; j--) {
			if (a[j] < a[j - 1]){
				swap(a[j], a[j - 1]);
				flag = true;
			}
		}
	}
	if (flag = false)
		return;
}

空间效率：仅使用了常数个辅助单元，空间复杂度为O(1)。

时间效率：最好情况下是初始序列有序，仅需比较n-1次，无需移动；最坏情况下是序列逆序，需要比较n-1次并且移动n-i次。从而平均时间复杂度为O(n^2)。

稳定性：冒泡排序是稳定的算法。

8.2.2 快速排序

在待排序列任选一个元素作为pivot，通常是第一个元素，通过一趟排序使得pivot分为两部分，左部分比pivot小，右部分比pivot大，pivot放在其最终位置上。

//快速排序
int Partition(ElemType a[], int low, int high)
{
	ElemType pivot = a[low];
	while (low < high) {
		while (low < high && a[high] > pivot)
			high--;				//以此找到比pivot小的元素
		a[low] = a[high];
		while (low < high && a[low] &