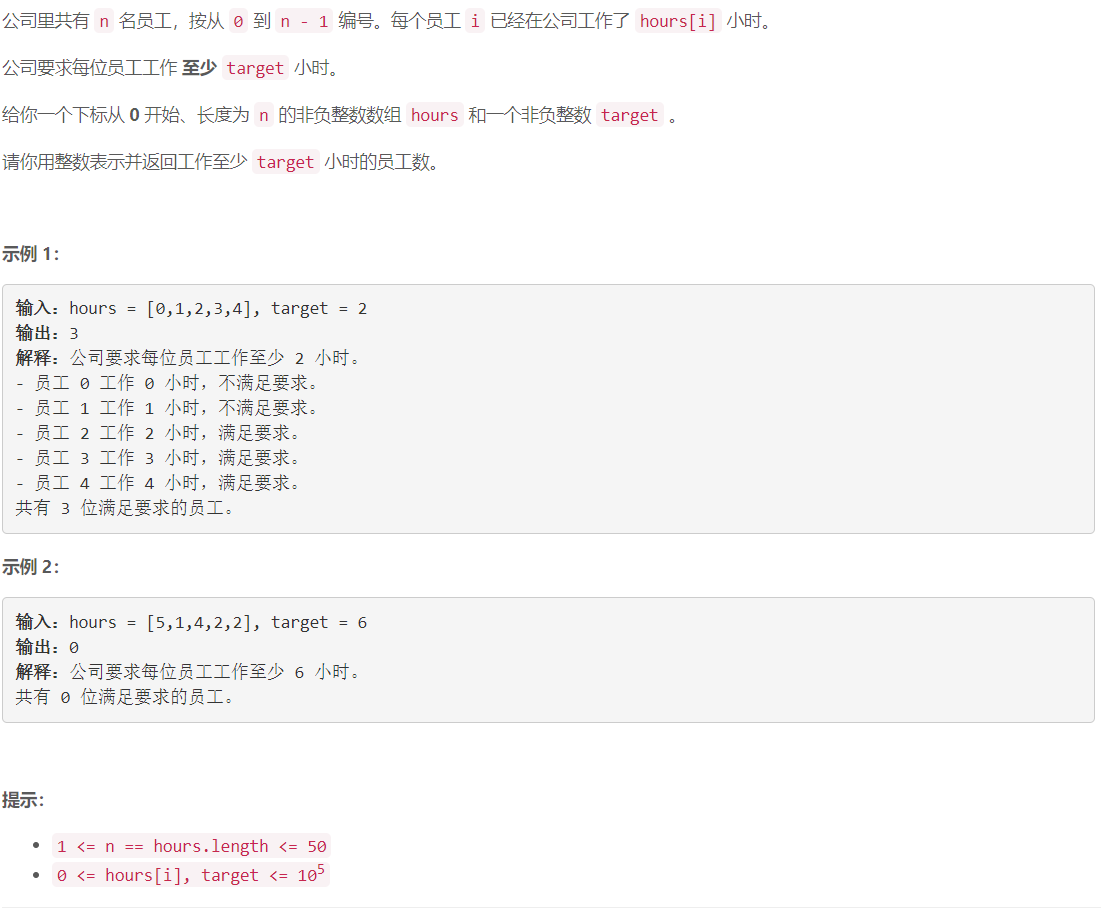
A 满足目标工作时长的员工数目

签到题

class Solution {
public:
    int numberOfEmployeesWhoMetTarget(vector<int> &hours, int target) {
        int res = 0;
        for (auto x: hours)
            if (x >= target)
                res++;
        return res;
    }
};

B 统计完全子数组的数目

枚举子数组：枚举子数组的长度，滑动窗口枚举定长子数组，同时维护数组中不同元素的数目

class Solution {
public:
    int countCompleteSubarrays(vector<int> &nums) {
        int n = nums.size();
        int mx = *max_element(nums.begin(), nums.end());
        vector<int> cnt(mx + 1);
        for (auto x: nums)
            cnt[x] = 1;
        int tar = accumulate(cnt.begin(), cnt.end(), 0);//数组中不同元素的数目
        int res = 0;
        for (int len = 1; len <= n; len++) {
            fill(cnt.begin(), cnt.end(), 0);
            int cur = 0;
            for (int i = 0; i < len - 1; i++)
                if (cnt[nums[i]]++ == 0)
                    cur++;
            for (int i = 0, j = i + len - 1; j < n; i++, j++) {
                if (cnt[nums[j]]++ == 0)
                    cur++;
                if (cur == tar)
                    res++;
                if (--cnt[nums[i]] == 0)
                    cur--;
            }
        }
        return res;
    }
};

C 包含三个字符串的最短字符串

枚举排列: 若$a,b,c$存在一个串是另一个串的子串的情况，则先删除$a,b,c$中的子串，再枚举剩余串的出现顺序，对于给定顺序每两个邻接串共用尽可能长的公共部分(eg：abc和bcd拼接共用bc)

class Solution {
public:

    string get(string &a, string &b) {//返回拼接a和b的最短串
        for (int k = min(b.size(), a.size()); k > 0; k--) {
            int i, j;
            for (i = a.size() - k, j = 0; j < k; i++, j++)
                if (a[i] != b[j])
                    break;
            if (j == k)
                return a + b.substr(k);
        }
        return a + b;
    }

    string minimumString(string a, string b, string c) {
        vector<string> li{a, b, c};
        sort(li.begin(), li.end(), [](string &s1, string &s2) { return s1.size() < s2.size(); });
        int cnt = 3;//剩余串的个数
        if (li[1].find(li[0]) != li[1].npos || li[2].find(li[0]) != li[2].npos) {//li[0]是某串的子串所以删除
            li.erase(li.begin());
            if (li[1].find(li[0]) != li[1].npos)//只剩1个串的情况
                return li[1];
            cnt = 2;
        }
        if (li[2].find(li[1]) != li[2].npos) {li[1]是某串的子串所以删除
            li.erase(li.begin() + 1);
            cnt = 2;
        }
        if (cnt == 2) {
            string s1 = get(li[0], li[1]);
            string s2 = get(li[1], li[0]);
            if (s1.size() != s2.size())
                return s1.size() < s2.size() ? s1 : s2;
            return s1 < s2 ? s1 : s2;
        }
        sort(li.begin(), li.end());
        string res(305, ' ');
        do {//枚举a,b,c串的排列顺序
            string t = get(li[0], li[1]);
            t = get(t, li[2]);
            if (t.size() < res.size() || t.size() == res.size() && t < res)
                res = t;
        } while (next_permutation(li.begin(), li.end()));
        return res;
    }
};

D 统计范围内的步进数字数目

定义$sum(s)$为闭区间$[1,s]$内的的步进数字数目，则区间$[low,high]$内的的步进数字数目为$sum[high]-sum[low]$（若$low$为步进数字则还要$+1$），定义$p_{loc,pre,val,eql}$为在 “当前待处理的下标为$loc$，前一位选择的数字（若存在）为$pre$，$val$：前面是否有选择数字（0：没有，1：有），$eql$：前面选择的数是否严格等于$s[0,loc-1]$（0：否，1：是）” 这种情况下可以构成多少个$[1,s]$内的步进数字，通过记忆化搜索进行计算。

class Solution {
public:
    typedef long long ll;
    ll mod = 1e9 + 7;

    int countSteppingNumbers(string low, string high) {
        int islow = 1;
        for (int i = 1; i < low.size(); i++)//判断low是否是步进数字
            if (abs(low[i] - low[i - 1]) != 1)
                islow = 0;
        return ((sum(high) - sum(low) + islow) % mod + mod) % mod;
    }

    ll sum(string &s) {
        int n = s.size();
        ll p[n + 1][10][2][2];
        memset(p, -1, sizeof(p));
        function<ll(int, int, int, int)> get = [&](int loc, int pre, int val, int eql) {
            if (p[loc][pre][val][eql] != -1)
                return p[loc][pre][val][eql];
            if (loc == n) {//已处理完每一位
                return p[loc][pre][val][eql] = val;
            }
            ll &cur = p[loc][pre][val][eql];
            cur = 0;
            if (val) {//前面有数字
                if (!eql) {//前面选择的数不严格等于s[0,loc-1]
                    if (pre != 0) {
                        cur += get(loc + 1, pre - 1, val, eql);
                        cur %= mod;
                    }
                    if (pre != 9) {
                        cur += get(loc + 1, pre + 1, val, eql);
                        cur %= mod;
                    }
                } else {//前面选择的数严格等于s[0,loc-1]
                    if (pre != 0 && pre - 1 <= s[loc] - '0') {
                        cur += get(loc + 1, pre - 1, val, pre - 1 == s[loc] - '0' ? 1 : 0);
                        cur %= mod;
                    }
                    if (pre != 9 && pre + 1 <= s[loc] - '0') {
                        cur += get(loc + 1, pre + 1, val, pre + 1 == s[loc] - '0' ? 1 : 0);
                        cur %= mod;
                    }
                }
            } else {//前面没有数字
                cur += get(loc + 1, 0, val, 0);
                if (!eql) {//前面选择的数不严格等于s[0,loc-1]
                    for (int i = 1; i <= 9; i++) {
                        cur += get(loc + 1, i, 1, 0);
                        cur %= mod;
                    }
                } else {//前面选择的数严格等于s[0,loc-1]
                    for (int i = 1; i <= s[loc] - '0'; i++) {
                        cur += get(loc + 1, i, 1, i == s[loc] - '0' ? 1 : 0);
                        cur %= mod;
                    }
                }
            }
            cur = (cur + mod) % mod;
            return cur;
        };
        return get(0, 0, 0, 1);
    }
};