动态规划
一、适合问题
存在若干步骤,并且每个步骤都面临若干选择。如果要求列出所有解就是回溯法。如果是求最优解(通常是最大值最小值)就用动态规划。
1.波契那亚数列和爬楼梯
2.背包问题
3.打家劫舍
4.股票问题
5.子序列问题
二、动态规划五部曲
1.dp数组及实际含义
数组dp用来保存每个问题结果的缓存,避免重复计算。
2.dp数组如何初始化
3.递推公式
用一个等式表示其中某一步的最优解和前面若干步的最优解的关系。
4.遍历顺序
for(i 背包)
for(j 物品)
5.打印dp数组
三、斐波那契数
斐波那契数,通常⽤ F(n) 表⽰,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后⾯的每⼀项数字都是前⾯两项数字的和。也就是:1 1 2 3 5 8
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给你n ,请计算 F(n) 。
1.确定dp[i]含义 dp[i]:第i个斐波那契数值为dp[i]。
2.递推公式 dp[i]=dp[i-1]+dp[i-2]
3.dp数组如何初始化 dp[0]=1 dp[1]=1
4.遍历顺序 从前到后(根据递推公式来的)
5.打印dp数组
四、爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的⽅法可以爬到楼顶呢?
注意:给定 n 是⼀个正整数。
⽰例 1:
输⼊: 2
输出: 2
解释: 有两种⽅法可以爬到楼顶。
1 阶 + 1 阶
2 阶
(依赖于前两阶)
几阶
1阶 1种
2阶 2种
3阶 3种
4阶 5种
1.确定dp[i]含义 dp[i]:到达i阶有dp[i]种方法
2.递推公式 dp[i]=dp[i-1]+dp[i-2](第i阶是由i-1阶和i-2阶得来的,因为只要再走一步or二步)
3.dp数组如何初始化 dp[0]=1 dp[1]=1 dp[2]=2
4.遍历顺序:从前到后
5.打印dp数组
五、使⽤最⼩花费爬楼梯
数组的每个下标作为⼀个阶梯,第 i 个阶梯对应着⼀个⾮负数的体⼒花费值 cost[i](下标从0 开始)。每当你爬上⼀个阶梯你都要花费对应的体⼒值,⼀旦⽀付了相应的体⼒值,你就可以选择向上爬⼀个阶梯或者爬两个阶梯。请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
⽰例 1:
输⼊:cost = [10, 15, 20]
输出:15
解释:最低花费是从 cost[1] 开始,然后⾛两步即可到阶梯顶,⼀共花费 15 。
解释:最低花费⽅式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,⼀共花费 6 。
1.确定dp[i]含义 dp[i]:到达第i个台阶的最小花费为dp[i]
2.递推公式dp[i]=min((dp[i-1]+cost[i-1]),(dp[i-2]+cost[i-2]))
dp[i]
dp[i-1]+cost[i-1]
dp[i-2]+cost[i-2]
3.dp数组如何初始化 dp[0]=0 dp[1]=0(一开始可以选择哪个台阶开始,还不用跳,都可以为0
4.遍历顺序:从前到后
5.打印dp数组
六、不同路径
⼀个机器⼈位于⼀个 m x n ⽹格的左上⾓ (起始点在下图中标记为 “Start” )。
机器⼈每次只能向下或者向右移动⼀步。机器⼈试图达到⽹格的右下⾓(在下图中标记为
“Finish” )。
问总共有多少条不同的路径?
⽰例 1:
1.确定dp[i][j]含义 dp[i][j]:到达位置(i,j)的路径数
2.递推公式dp[i][j]=dp[i][j-1]+dp[i-1][j]
3.dp数组如何初始化 (第一行跟第一列必须初始化,如果这两个没有初始化没办法接下来计算)
dp[0][j]=1
dp[i][0]=1
for (int i=0;i<m;i++) dp[i][0]=1;
for(int j=0;j<n;j++)dp[0][j]=1;
4.遍历顺序:从上到下,从左到右遍历
5.打印dp数组
六、不同路径II
⼀个机器⼈位于⼀个 m x n ⽹格的左上⾓ (起始点在下图中标记为“Start” )。
机器⼈每次只能向下或者向右移动⼀步。机器⼈试图达到⽹格的右下⾓(在下图中标记为
“Finish”)。
现在考虑⽹格中有障碍物。那么从左上⾓到右下⾓将会有多少条不同的路径?
输⼊:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:
3x3 ⽹格的正中间有⼀个障碍物。
从左上⾓到右下⾓⼀共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
1.确定dp[i]含义 dp[i]:到达i阶有dp[i]种方法
2.递推公式dp[i][j]=dp[i][j-1]+dp[i-1][j](多一个条件就是遇到障碍不用继续推导)
if(obs[i][j]==0) 当遇不上障碍时开始推导。
3.dp数组如何初始化 (第一行跟第一列必须初始化,如果这两个没有初始化没办法接下来计算)但是如果这两行遇到障碍,之后都是0
for(int i=0;i<m&&dos[i][0]==0;i++) dp[i][0]=1;
for(int j=0;j<m&&dos[i][0]==0;i++) dp[0][j]=1;
4.遍历顺序:从上到下,从左到右遍历
5.打印dp数组
七、整数拆分
给定⼀个正整数 n,将其拆分为⾄少两个正整数的和,并使这些整数的乘积最⼤化。 返回
你可以获得的最⼤乘积。
⽰例 1:
输⼊: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
1.确定dp[i]含义 dp[i]:是给定一个数i,能拆得最大乘积
j×(i-j) 拆成2个
j×dp[i-j]拆成3个或3个以上
2.递推公式dp[i]=max(j*(i-j),j*dp[i-j])
3.dp数组如何初始化
dp[0]=0(没有意义)
dp[1]=0(没有意义)
dp[2]=1
3.dp数组如何初始化
从dp[3]开始,因为dp[0],dp[1],dp[2]都已经初始化了。
for(i=3;i<=n;i++)
for(j=1;j<i;j++)
dp[i]=max(j*(i-j),j*dp[i-j],dp[i])
4.遍历顺序
4.打印dp数组
八、不同的二叉搜索树
1.确定dp[i]含义 dp[i]:1到i为节点组成的⼆叉搜索树的个数为dp[i]。
2.递推公式dp[i]=max(j*(i-j),j*dp[i-j])
在上⾯的分析中,其实已经看出其递推关系, dp[i] += dp[以j为头结点左⼦树节点数量] *
dp[以j为头结点右⼦树节点数量]
j相当于是头结点的元素,从1遍历到i为⽌。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左⼦树节点数量,i-j 为以j为
头结点右⼦树节点数量
3.dp数组如何初始化
dp[0]=1(空树)
4.遍历顺序:从小到大
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
dp[i]+=dp[j-1]*dp[i-j];
5.打印dp数组
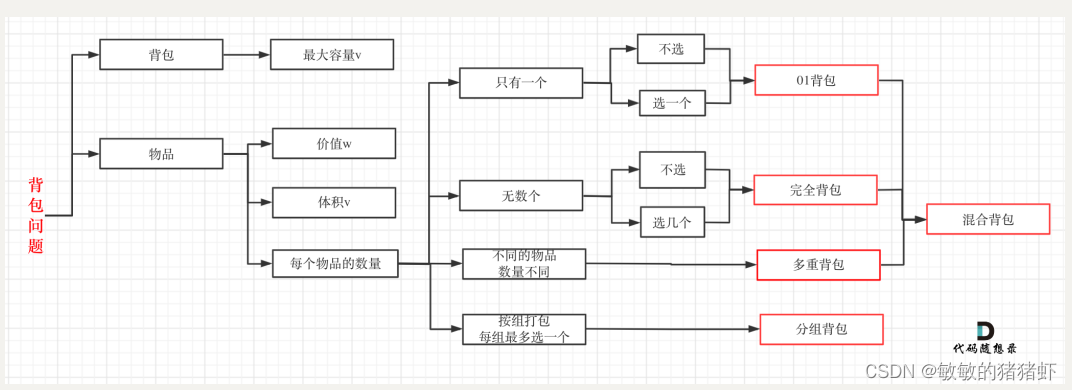
九、背包问题
1.确定dp[i][j]含义 dp[i][j]:即dp[i][j] 表⽰从下标为[0-i]的物品⾥任意取,放进容量为j的背包,价值总和最⼤是多少
2.递推公式
对于每个物品有两种选择:放与不放
不放物品i:dp[i-1][j]
放物品i:dp[i-1][j-weight]+value
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight]+value)
3.dp数组如何初始化
递推公式是由上一行推导来的,所以要初始化第一行和第一列。第一列都为0,因为代表0重量情况下无法装入任何物品。第一行如果编号i物品可以装入,则是该物品的价值,如果重量导致不能装入则为0
4.遍历顺序:可以先遍历物品再遍历背包,也可以先遍历背包再遍历物品
for()物品
for()背包
二维数组无所谓谁先谁后,但是一维滚动数组就有顺序
十、背包问题-滚动数组
1.确定dp[j]含义 :在⼀维dp数组中,dp[j]表⽰:容量为j的背包,所背的物品价值可以最⼤为dp[j]。
2.递推公式
dp[j]=max(dp[j],dp[j-weight[i]]+value[i])
可以看出相对于⼆维dp数组的写法,就是把dp[i][j]中i的维度去掉了。
3.dp数组如何初始化
关于初始化,⼀定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
dp[j]表⽰:容量为j的背包,所背的物品价值可以最⼤为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最⼤价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);看⼀下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候⼀定是取价值最⼤的数,如果题⽬给的价值都是正整数那么⾮0下标都
初始化为0就可以了,如果题⽬给的价值有负数,那么⾮0下标就要初始化为负⽆穷。
这样才能让dp数组在递归公式的过程中取的最⼤的价值,⽽不是被初始值覆盖了。
那么我假设物品价值都是⼤于0的,所以dp数组初始化的时候,都初始为0就可以了。
4.遍历顺序:一维dp遍历,背包从大到小,倒序遍历为了保证物品i只被放入一次。并且只能先物品后背包容量。
for(int i = 0; i < weight.size(); i++) {
// 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) {
// 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
5.打印dp数组
十一、分割等和子集
给定⼀个只包含正整数的⾮空数组。是否可以将这个数组分割成两个⼦集,使得两个⼦集的
元素和相等。
注意:
每个数组中的元素不会超过 100
数组的⼤⼩不会超过 200
⽰例 1:
输⼊: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
抽象成背包问题,容量和价值一样,比如把容量11的背包装满之后价值也是11.
1.确定dp[j]含义 :在⼀维dp数组中,dp[j]表⽰:容量为j的背包,所背的物品价值可以最⼤为dp[j]。
2.递推公式
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weightt[i]+value[i])
降维了
dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
3.dp数组如何初始化
dp[0]=0
整个dp数组初始化为0
4.遍历顺序:先遍历物品后遍历背包,背包是倒叙防止重复
// 开始 01背包
for(int i = 0; i < nums.size(); i++) {
for(int j = target; j >= nums[i]; j--) {
// 每⼀个元素⼀定是不可重复放
⼊,所以从⼤到⼩遍历
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
5.打印dp数组
十二、最后⼀块⽯头的重量II
有⼀堆⽯头,每块⽯头的重量都是正整数。
每⼀回合,从中选出任意两块⽯头,然后将它们⼀起粉碎。假设⽯头的重量分别为 x 和 y,
且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块⽯头都会被完全粉碎;
如果 x != y,那么重量为 x 的⽯头将会完全粉碎,⽽重量为 y 的⽯头新重量为 y-x。
最后,最多只会剩下⼀块⽯头。返回此⽯头最⼩的可能重量。如果没有⽯头剩下,就返回
0。
⽰例:
输⼊:[2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
1.确定dp[j]含义 :装满容量为j的最大重量是dp[j]
2.递推公式
dp[j]=max[dp[j],dp[j-weight[i]+value[i]]]
3.dp数组如何初始化
dp[0]=0
整个dp数组初始化为0
定义多大的数组,sum/2
最后结果是sum-dp[target]-dp[target]
4.遍历顺序:先遍历物品后遍历背包,背包是倒叙防止重复
5.打印dp数组
十三、目标和
给定⼀个⾮负整数数组,a1, a2, …, an, 和⼀个⽬标数,S。现在你有两个符号 + 和 -。对于
数组中的任意⼀个整数,你都可以从 + 或 -中选择⼀个符号添加在前⾯。
返回可以使最终数组和为⽬标数 S 的所有添加符号的⽅法数。
⽰例:
输⼊:nums: [1, 1, 1, 1, 1], S: 3
输出:5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
⼀共有5种⽅法让最终⽬标和为3。
left+right=Sum
left-right=target
right=Sum-left
left-(Sum-left)=target
left=(target+Sum)/2
1.确定dp[j]含义 :装满容量为j,有dp[j]种方法
2.递推公式
dp[j]+=dp[j-num[i]]
3.dp数组如何初始化
从递归公式可以看出,在初始化的时候dp[0] ⼀定要初始化为1,因为dp[0]是在公式中⼀切
递推结果的起源,如果dp[0]是0的话,递归结果将都是0。
dp[0] = 1,理论上也很好解释,装满容量为0的背包,有1种⽅法,就是装0件物品。
dp[j]其他下标对应的数值应该初始化为0,从递归公式也可以看出,dp[j]要保证是0的初始
值,才能正确的由dp[j - nums[i]]推导出来。
4.遍历顺序:先遍历物品后遍历背包,背包是倒叙防止重复
for(i=0;i<nums.size;i++)
for(j=bagsize;j>=nums[i];j–)
十四、一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ,因此答案是 4 。 其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = [“10”, “0”, “1”], m = 1, n = 1
输出:2
解释:最大的子集是 {“0”, “1”} ,所以答案是 2 。
提示:
1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100
1.确定dp[i][j]含义 :最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
思路:一个容器有两个维度。m和n。
2.递推公式
dp[i][j]=max(dp[i-x][j-y]+1,dp[i][j])
3.dp数组如何初始化
dp[0][0]=0
非0也初始化为0
4.遍历顺序:先遍历物品后遍历背包,背包是倒叙防止重复
class Solution{
public int findMaxForm(String[] strs,int m,int n){
int[][] dp=new [m+1][n+1];
int oneNum,zeroNum;
for (String str:strs){
oneNum=0;
zeroNum=0;
for(char ch:str.toCharArray()){
if(ch=='0'){
zeroNum++;
}else{
oneNum++;
}
}
//倒序遍历
for(int i=m;i>=zeroNum;i--){
for(int j=n;j>=oneNum;j--){
dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);
}
}
}
return dp[m][n];
}
}
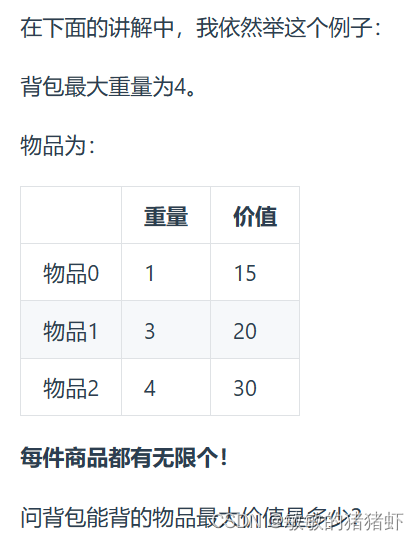
十五、完全背包理论
完全背包和01背包唯一不同的地方,每种物品有无限件。在代码中体现在遍历顺序上。
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。遍历物品在外层循环,遍历背包容量在内层循环。
private static void testCompletePack(){
int[] weight={
1,3,4};
int[] value={
15,20,30};
int bagWeight=4;
int[] dp=new int[bagWeight+1];
for (int i=0;i<weight.length;i++){
for(int j=weight[i];j<=bagWeight;j++){
dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i]);
}
}
for(int maxValue:dp){
System.out.println(maxValue+" ");
}
}
十六、零钱兑换2
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
1.确定dp[j]含义 :以总金额j的最多硬币组合数
2.递推公式
dp[j]+=dp[j-conins[i]]
求装满背包有几种方法,公式都是:dp[j] += dp[j - nums[i]];
2.初始化dp数组
首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。
3.遍历顺序
求组合就先遍历物品,求排序就先遍历背包
class Solution{
public int change(int amount,int[] coins){
int[] dp=new int[amount+1];
dp[0]=1;
for(int i=0;i<coins.length;i++){
for(int j=coins[i];j<=amount;j++){
dp[j]+=dp[j-coins[i]];
}
}
return dp[amount];
}
}
十七、组合总和
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
nums = [1, 2, 3]
target = 4
所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
1.确定dp[i]含义 :凑成目标i的组合数总和
2.递推公式
dp[i]+=dp[i-nums[j]]
3.dp数组如何初始化
因为递推公式dp[i] += dp[i - nums[j]]的缘故,dp[0]要初始化为1,这样递归其他dp[i]的时候才会有数值基础。
至于非0下标的dp[i]应该初始为多少呢?
初始化为0,这样才不会影响dp[i]累加所有的dp[i - nums[j]]。
4.遍历顺序:因为求的是排列,所以先背包后物品
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution{
int[] dp=new int[target+1];
do[0]=1;
for(int i=0;i<=target;i++){
for(int j=0;j<=nums.length;j++){
if(i>=nums[j]){
dp[i<