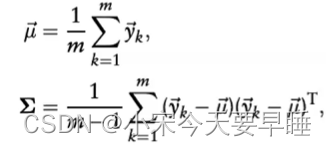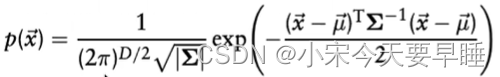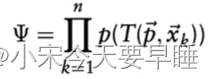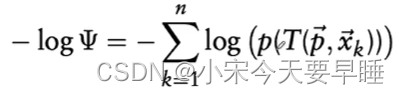文章目录
0 学习本算法需要具备的基础知识
- 非线性优化算法:牛顿法(《视觉SLAM十四讲》第6讲有介绍)
- 高斯概率密度函数的表示形式
- 旋转矩阵、欧拉角向旋转矩阵的转化(《视觉SLAM十四讲》第3讲有介绍)
1 算法要解决的问题、核心思想及主要流程
1.1 要解决的问题
求解待匹配点云(表示为
x
i
x_i
xi,i代表点云中的第i个点
i
=
1
,
2...
n
i=1,2...n
i=1,2...n)坐标系和原点云(表示为
y
i
y_i
yi)坐标系之间的坐标转换关系
p
p
p(
p
=
[
ϕ
x
,
ϕ
y
,
ϕ
z
,
t
x
,
t
y
,
t
z
]
p=[\phi_x, \phi_y, \phi_z,t_x, t_y, t_z]
p=[ϕx,ϕy,ϕz,tx,ty,tz])。使得求解得到的
p
p
p满足以下方程
y
i
=
r
o
t
(
ϕ
x
,
x
)
r
o
t
(
ϕ
y
,
y
)
r
o
t
(
ϕ
z
,
z
)
x
i
+
[
t
x
,
t
y
,
t
z
]
T
y_i = rot(\phi_x,x)rot(\phi_y,y)rot(\phi_z,z)x_i+[t_x, t_y, t_z]^T
yi=rot(ϕx,x)rot(ϕy,y)rot(ϕz,z)xi+[tx,ty,tz]T
其中
- r o t ( ϕ x , x ) rot(\phi_x,x) rot(ϕx,x)表示为绕x轴旋转 ϕ x \phi_x ϕx度的旋转矩阵
为方面之后描述,记:
T
(
p
,
x
i
)
=
r
o
t
(
ϕ
x
,
x
)
r
o
t
(
ϕ
y
,
y
)
r
o
t
(
ϕ
z
,
z
)
x
i
+
[
t
x
,
t
y
,
t
z
]
T
T(p,x_i) = rot(\phi_x,x)rot(\phi_y,y)rot(\phi_z,z)x_i+[t_x, t_y, t_z]^T
T(p,xi)=rot(ϕx,x)rot(ϕy,y)rot(ϕz,z)xi+[tx,ty,tz]T
1.2 核心思想
NDT算法将原点云通过多个高斯分布进行描述,点密集的地方概率密度大,稀疏的地方概率密度小。通过坐标转换关系,将待匹配点云转换到原点云坐标系下,将转换后的点云带入到之前得到的概率密度函数中,就会得到一个整体点云的概率值。优化坐标转换关系,使得这个概率值最大。
1.3 主要流程
1.3.1 原点云的概率密度表示
- 原点云进行栅格划分
- 计算每个栅格中点云的均值和方差,这样就会得到一个高斯分布,用这个高斯分布描述这个栅格中的点云分布情况
1.3.2 构造优化函数
- 构建关于 p p p( p = [ ϕ x , ϕ y , ϕ z , t x , t y , t z ] p=[\phi_x, \phi_y, \phi_z,t_x, t_y, t_z] p=[ϕx,ϕy,ϕz,tx,ty,tz])的优化函数,该优化函数为待匹配点云 x i x_i xi关于上述高斯分布的一个整体概率方程,并进行一些近似
1.3.3 迭代优化
- 对上述方程应用牛顿法优化
p
p
p(
p
=
[
ϕ
x
,
ϕ
y
,
ϕ
z
,
t
x
,
t
y
,
t
z
]
p=[\phi_x, \phi_y, \phi_z,t_x, t_y, t_z]
p=[ϕx,ϕy,ϕz,tx,ty,tz]),同时为了减少计算,对优化函数的一阶导数和二阶导数进行近似
大概流程可简化为如下图:
2 详细流程
2.1 原点云的概率密度表示:
- 原点云做栅格划分,如果栅格中的点少于五个就认为这个栅格里边没有点
- 计算每个栅格中点的高斯分布,每个高斯分布的均值和方差的计算公式如下:
- 基于每个栅格中的高斯分布,我们就可以推测原点云在空间任意位置存在一个点的概率值,记作
p
(
x
)
p(x)
p(x)。
2.2 构造优化函数,优化变量 p , ( p = [ ϕ x , ϕ y , ϕ z , t x , t y , t z ] ) p,(p=[\phi_x, \phi_y, \phi_z,t_x, t_y, t_z]) p,(p=[ϕx,ϕy,ϕz,tx,ty,tz])
- 计算在当前旋转量和平移量
p
=
[
ϕ
x
,
ϕ
y
,
ϕ
z
,
t
x
,
t
y
,
t
z
]
p=[\phi_x, \phi_y, \phi_z,t_x, t_y, t_z]
p=[ϕx,ϕy,ϕz,tx,ty,tz]的作用下,待匹配点云
x
i
x_i
xi在原点云坐标系下的分布情况,即
x i ′ = T ( p , x i ) x_i^{'}=T(p,x_i) xi′=T(p,xi) - 计算
x
i
′
x_i^{'}
xi′所处的栅格,根据初始化步骤中得到的该栅格处的概率密度函数
p
(
x
)
p(x)
p(x),计算
x
i
′
(
i
=
1
,
2...
n
)
x_i^{'}(i = 1,2...n)
xi′(i=1,2...n)的整体概率值,即为
此时,我们就把配准问题转化成了一个最大似然估计问题,我们下一步要做的就是就是优化 p ( p = [ ϕ x , ϕ y , ϕ z , t x , t y , t z ] ) p(p=[\phi_x, \phi_y, \phi_z,t_x, t_y, t_z]) p(p=[ϕx,ϕy,ϕz,tx,ty,tz]),使得上述概率值最大即可。但是考虑到外点及计算复杂度的问题,还需要调节目标优化函数 Ψ \Psi Ψ的结构,并取一些近似。 - 调节1,为优化函数增加一个"log"帽子:为了去掉上述概率方程中的exp的连乘(高斯分布包含e的指数项),从而简化求导形式。我们在整体的概率方程前加入一个log函数,这样就能把exp给抵消掉。这时候最大似然估计就变成了最小化如下方程:
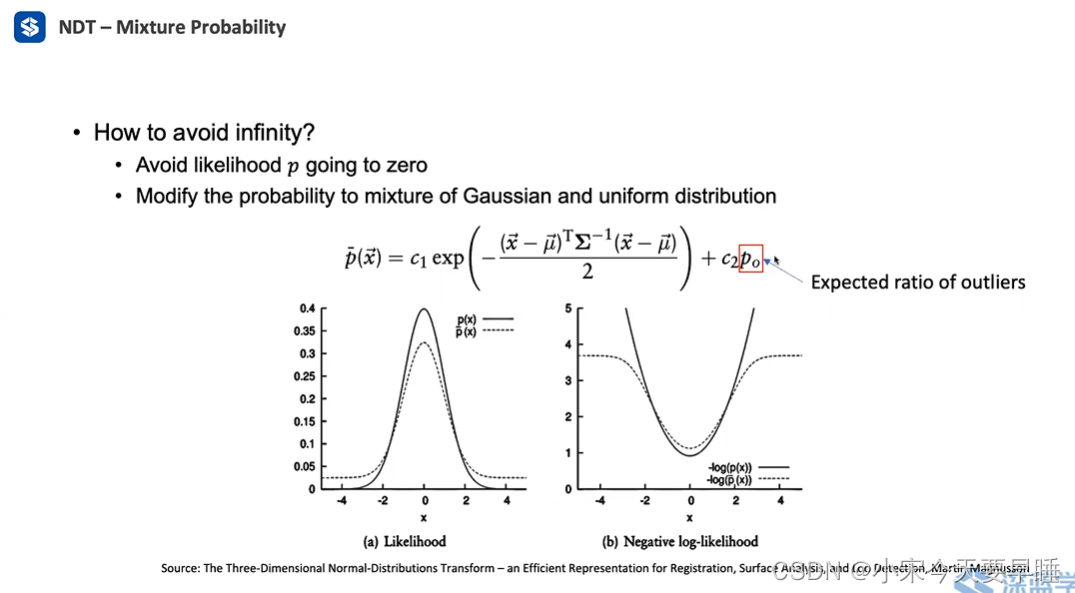
- 调节2:为优化函数增加一个常数项,即:
−
l
o
g
(
p
(
x
o
u
t
l
i
e
r
)
+
c
)
-log(p(x_{outlier}) + c)
−log(p(xoutlier)+c):当存在外点
x
o
u
t
l
i
e
r
x_{outlier}
xoutlier时,
p
(
x
o
u
t
l
i
e
r
)
p(x_{outlier})
p(xoutlier)趋近于0,这就导致
l
o
g
(
p
(
x
o
u
t
l
i
e
r
)
)
log(p(x_{outlier}))
log(p(xoutlier))趋近于无穷,使得优化主要考虑的对象变为外点,导致优化不收敛。引入一个常数项后,优化方程变为如下形式:
−
l
o
g
(
c
1
p
(
x
o
u
t
l
i
e
r
)
+
c
2
p
0
)
-log(c_1p(x_{outlier}) + c_2p_0)
−log(c1p(xoutlier)+c2p0),当p(x_{outlier})趋近于0时,优化函数将会趋近于一个常数log(c_2p_0),而不是无穷,使得优化可以正常进行。加入常数项前后的优化函数的分布变化如下图所示:
在引入常数项后,还额外引入了三个超参数,分别是 c 1 , c 2 , p 0 c_1,c_2,p_0 c1,c2,p0,由于 c 2 , p 0 c_2,p_0 c2,p0为同一项,因此可以看成一个参数,记作 c 2 c_2 c2。这三个参数的调节方法可以有如下两个方法,简单起见可以用第二个方法。
- 优化函数的近似:为了便于优化求导,我们可以将优化函数近似成一个”倒扣“的高斯分布,即
− log p ˉ ( x ⃗ ) = − log ( c 1 exp ( − ( x ⃗ − μ ⃗ ) T Σ − 1 ( x ⃗ − μ ⃗ ) 2 ) + c 2 ) -\log \bar{p}(\vec{x})=-\log \left(c_{1} \exp \left(-\frac{(\vec{x}-\vec{\mu})^{T} \Sigma^{-1}(\vec{x}-\vec{\mu})}{2}\right)+c_{2}\right) −logpˉ(x)=−log(c1exp(−2(x−μ)TΣ−1(x−μ))+c2)
可近似看成
p ~ ( x ⃗ ) = d 1 exp ( − d 2 ( x ⃗ − μ ⃗ ) T Σ − 1 ( x ⃗ − μ ⃗ ) 2 ) + d 3 \tilde{p}(\vec{x})=d_{1} \exp \left(-\frac{d_{2}(\vec{x}-\vec{\mu})^{T} \Sigma^{-1}(\vec{x}-\vec{\mu})}{2}\right)+d_{3} p~(x)=d1exp(−2d2(x−μ)TΣ−1(x−μ))+d3.
上式中,含有三个未知的超参数 d 1 , d 2 , d 3 d_1,d_2,d_3 d1,d2,d3,可以在概率密度函数中采样三个点进行确定,如下图所示:
经过上述几步的调节和近似后,我们最终需要优化的函数可以表示成如下形式:
s ( p ⃗ ) = ∑ k = 1 n p ~ ( T ( p ⃗ , x ⃗ k ) ) = ∑ k = 1 n d 1 exp ( − d 2 ( T ( p ⃗ , x ⃗ k ) − μ ⃗ k ) T Σ k − 1 ( T ( p ⃗ , x ⃗ k ) − μ ⃗ k ) 2 ) + d 3 s(\vec{p})=\sum_{k=1}^{n} \tilde{p}\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)=\sum_{k=1}^{n} d_{1} \exp \left(-\frac{d_{2}\left(T\left(\vec{p}, \vec{x}_{k}\right)-\vec{\mu}_{k}\right)^{T} \Sigma_{\mathrm{k}}^{-1}\left(T\left(\vec{p}, \vec{x}_{k}\right)-\vec{\mu}_{k}\right)}{2}\right)+d_{3} s(p)=k=1∑np~(T(p,xk))=k=1∑nd1exp(−2d2(T(p,xk)−μk)TΣk−1(T(p,xk)−μk))+d3
2.3 应用牛顿法迭代优化上述优化函数
- 优化函数一阶偏导 g g g和二阶偏导 H H H计算:牛顿法是将一个非线性函数应用二阶泰勒展开进行近似,然后再求解极值点。因此,在开始牛顿法优化前,需要先计算优化函数的一阶偏导和二阶偏导。优化函数的一阶偏导和二阶偏导如下:
- 一阶偏导
g
i
g_{i}
gi:
g i = δ s δ p i = ∑ k = 1 n d 1 d 2 x ⃗ k ′ T Σ k − 1 δ x ⃗ k ′ δ p i exp ( − d 2 2 x ⃗ k ′ T Σ k − 1 x ⃗ k ′ ) g_{i}=\frac{\delta s}{\delta p_{i}}=\sum_{k=1}^{n} d_{1} d_{2} \vec{x}_{k}^{\prime}{ }^{\mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}} \exp \left(\frac{-d_{2}}{2} \vec{x}_{k}^{\prime}{ }^{\mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1} \vec{x}_{k}^{\prime}\right) gi=δpiδs=k=1∑nd1d2xk′TΣk−1δpiδxk′exp(2−d2xk′TΣk−1xk′) - 二阶偏导
H
i
j
H_{i j}
Hij
H i j = δ 2 s δ p i δ p j = ∑ k = 1 n d 1 d 2 exp ( − d 2 2 x ⃗ k ′ T Σ k − 1 x ⃗ k ′ ) ( − d 2 ( x ⃗ k ′ Σ k − 1 δ x ⃗ k ′ δ p i ) ( x ⃗ k ′ Σ k − 1 δ x ⃗ k ′ δ p j ) + x ⃗ k ′ Σ k − 1 δ 2 x ⃗ k ′ δ p i δ p j + δ x ⃗ k ′ δ p j Σ k − 1 δ x ⃗ k ′ δ p i ) H_{i j}=\frac{\delta^{2} s}{\delta p_{i} \delta p_{j}}=\sum_{k=1}^{n} d_{1} d_{2} \exp \left(\frac{-d_{2}}{2} \vec{x}_{k}^{'\mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1} \vec{x}_{k}^{\prime}\right)\left(-d_{2}\left(\vec{x}_{k}^{\prime} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}}\right)\left(\vec{x}_{k}^{\prime} \Sigma_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{j}}\right)+\vec{x}_{k}^{\prime} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta^{2} \vec{x}_{k}^{\prime}}{\delta p_{i} \delta p_{j}}+\frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{j}} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}}\right) Hij=δpiδpjδ2s=k=1∑nd1d2exp(2−d2xk′TΣk−1xk′)(−d2(xk′Σk−1δpiδxk′)(xk′Σk−1δpjδxk′)+xk′Σk−1δpiδpjδ2xk′+δpjδxk′Σk−1δpiδxk′)
上式中,
x
⃗
′
=
T
(
p
,
x
i
⃗
)
\vec{x}^{'} = T(p,\vec{x_i})
x′=T(p,xi)
上式中,
x
⃗
′
\vec{x}^{'}
x′关于
p
p
p的一阶
δ
x
⃗
k
′
δ
p
i
\frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}}
δpiδxk′、二阶偏导数
δ
x
⃗
k
′
δ
p
i
δ
p
j
\frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i} \delta p_{j}}
δpiδpjδxk′可表示成如下形式(这一步由于没做近似,关于因此比较乱,其实可以跳过不看):
一阶偏导数:
二阶偏导数:
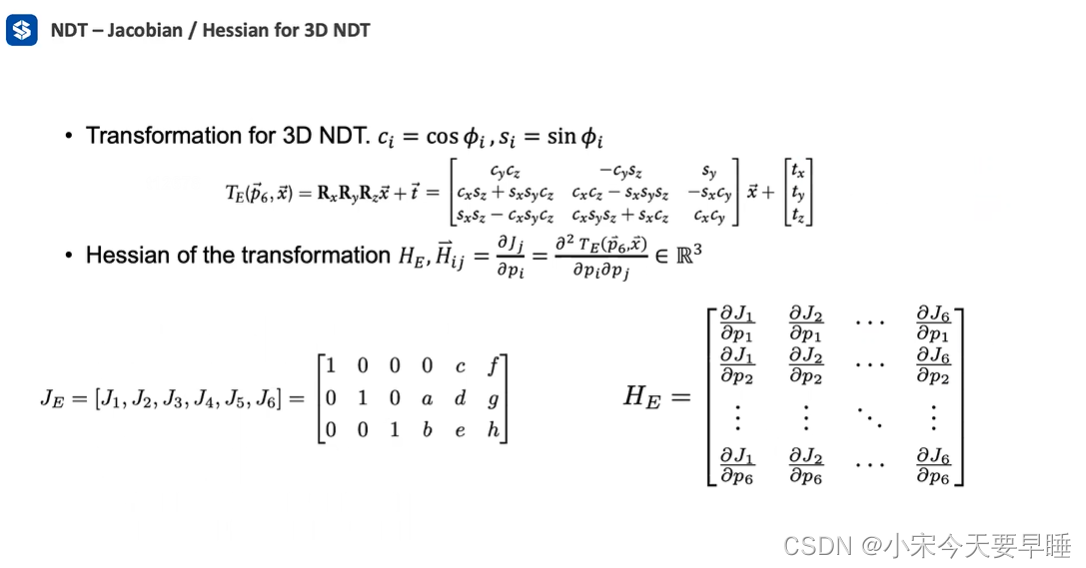
- 一阶偏导和二阶偏导的近似:我们假设关于
p
p
p的
ϕ
x
,
ϕ
y
,
ϕ
z
\phi_x, \phi_y, \phi_z
ϕx,ϕy,ϕz都是一个比较小的量,则可以做这样的近似:
s
i
n
(
ϕ
)
=
ϕ
,
c
o
s
(
ϕ
)
=
1
,
ϕ
2
=
0
sin(\phi) = \phi, cos(\phi)=1, \phi^2=0
sin(ϕ)=ϕ,cos(ϕ)=1,ϕ2=0,经过这样的简化之后,坐标变换矩阵
T
T
T,
x
⃗
′
\vec{x}^{'}
x′关于
p
p
p的一阶
δ
x
⃗
k
′
δ
p
i
\frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}}
δpiδxk′、二阶偏导数
δ
x
⃗
k
′
δ
p
i
δ
p
j
\frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i} \delta p_{j}}
δpiδpjδxk′可表示成如下形式:
到这里目前有个疑问(这里优化的对象是 p p p本身,还是相当于给 p p p加了一个左扰动,优化 δ p \delta p δp)?
- 计算完偏导数之后,可以应用牛顿法求解出 δ p \delta p δp = H − 1 g =H^{-1}g =H−1g
- 更新 p p p = p + δ p =p+\delta p =p+δp,回到第9步,再次开启下一轮迭代
相关源代码
相关源代码的解析可以看参考链接