深入探讨A*算法:寻找最佳路径的智能之旅
1. 引言
A*算法是一种强大的启发式搜索算法,可应用于路径规划和图搜索问题。无论是在游戏开发、机器人导航还是地理信息系统中,A算法都是一个重要而高效的工具。 在本文中,我们将深入探讨A算法的原理、应用和实现。
基本的深度优先DFS和广度优先算法BFS执行无信息搜索。它们详尽地搜索树或图中的节点。它们不会估计到达目标的特定路线的成本。当他们第一次找到目标时,他们就会停下来。它们不一定能找到到达目标的最短路径。
不同的是,A*算法会评估在搜索的每个阶段探索的最佳方向,而不是按照预定的顺序盲目地搜索每个可用的路径,可以找到最佳路径。
2. A*算法的基本原理
A*算法是一种启发式搜索算法,用于寻找从起始节点到目标节点的最短路径。它结合了实际成本(g值)和 启发式估计成本(h值)来评估路径的优劣。
- g值:从起始节点到当前节点的实际成本。
- h值:从当前节点到目标节点的估计成本(启发式估算)。
A*算法使用以下公式计算节点的代价函数 f f f的值,以决定下一个要扩展的节点:
f ( n ) = g ( n ) + h ( n ) f(n) = g(n) + h(n) f(n)=g(n)+h(n)
其中, f ( n ) f(n) f(n)是节点 n n n的估计总成本。A*算法不断选择具有最小代价函数 f f f值的节点进行扩展,直到找到目标节点或确定没有可行解为止。
3. A*算法的步骤
A*算法可以分为以下步骤:
- 初始化:将起始节点添加到开放列表,并将其 g g g值设置为0。
- 循环:不断执行以下步骤直到找到目标节点或开放列表为空。
a. 从开放列表中选择具有最小代价函数 f f f值的节点进行扩展。
b. 将该节点从开放列表移到关闭列表。
c. 如果该节点为目标点,则退出循环
d. 对该节点的邻居节点进行评估:- 如果邻居节点不在开放列表或关闭列表中,将其添加到开放列表,并计算其g值和h值。
- 如果邻居节点已在开放列表中,检查是否通过当前节点获得更低的g值。如果是,更新g值。
- 如果开放列表为空,且未找到目标节点,则无解。
3. A*算法的优点和适用性
A*算法有以下优点:
- 最优性:如果启发式估计函数h是一致的,A*算法将找到最佳路径。
- 适应性:A*算法适用于多种应用领域,因为可以根据问题调整启发式估计函数。
- 可控性:通过调整启发式估计函数的权重,可以在速度和最优性之间取得平衡。
A*算法适用于以下问题:
- 地图导航和游戏路径规划。
- 机器人运动规划,例如无人机导航。
- 博弈搜索等人工智能领域。
- 计算机视觉中的对象识别与追踪。
- 自然语言处理中的语法分析。
4. A*算法的实现
A*算法的实现通常涉及使用优先队列来管理开放列表,并定义适合问题的启发式估计函数h。启发式估计函数的选择对算法性能至关重要,通常需要根据具体问题进行调整。
4.1 A*算法的伪代码示例:
function AStar(start, goal)
openList := {start}
closedList := {}
while openList is not empty
current := node in openList with the lowest f value
if current == goal
return reconstructPath(current)
remove current from openList
add current to closedList
for each neighbor of current
if neighbor is in closedList
continue
tentativeG := g(current) + distance(current, neighbor)
if neighbor is not in openList or tentativeG < g(neighbor)
set g(neighbor) to tentativeG
set h(neighbor) to heuristic(neighbor, goal)
set f(neighbor) to g(neighbor) + h(neighbor)
if neighbor is not in openList
add neighbor to openList
return failure
4.2 A*算法的C++代码示例:
bool Astar(Map &map)
{
vector<Point> Openlist;
vector<Point> Closedlist;
Point start,end;
start.x = map.startx;
start.y = map.starty;
end.x = map.endx;
end.y = map.endy;
start.g = 0;
start.h = abs(end.x -start.x) +abs(end.y -start.y);
start.f = start.g+start.h;
start.father = -1;
Openlist.push_back(start);
while(~Openlist.empty())
{
//查找开放列表中最优节点,删除开放列表中该节点,并将其插入关闭列表
Point optimalPoint;
findOptimalPoint(optimalPoint, Openlist,Closedlist);
//如果该点为目标点,退出
if (optimalPoint.x == map.endx && optimalPoint.y == map.endy)
{
cout << "找到啦"<<endl;
int i = Closedlist.size()-1;
while(i>=0)
{
map.Info[Closedlist[i].x][Closedlist[i].y] = 6;
i = Closedlist[i].father;
}
return 1;
}
//探索有效最优节点的邻居
vector<Point> NeighborPoint;
findNeighborPoint(optimalPoint,NeighborPoint,Closedlist,map);
//更新邻居节点数据
for(int i=0; i<NeighborPoint.size();i++)
{
Point point = NeighborPoint[i];
int g = optimalPoint.g + abs(optimalPoint.x-point.x)+abs(optimalPoint.y-point.y);
int h = abs(map.endx-point.x)+abs(map.endy-point.y);
int f = g+h;
//查看是否位于开放列表
bool inOpenlist;
for(auto iter=Openlist.begin();iter!=Openlist.end();iter++)
{
if(point.x == iter->x && point.y == iter->y)
{//在开放列表
if (iter->f > f)
{
iter->f = f;
iter->g = g;
iter->h = h;
iter->father = Closedlist.size()-1;
inOpenlist = 0;
}
}
}
if(~inOpenlist)
{//不在开放列表
point.f = f;
point.g = g;
point.h = h;
point.father = Closedlist.size()-1;
Openlist.push_back(point);
}
}
}
return 0;
}
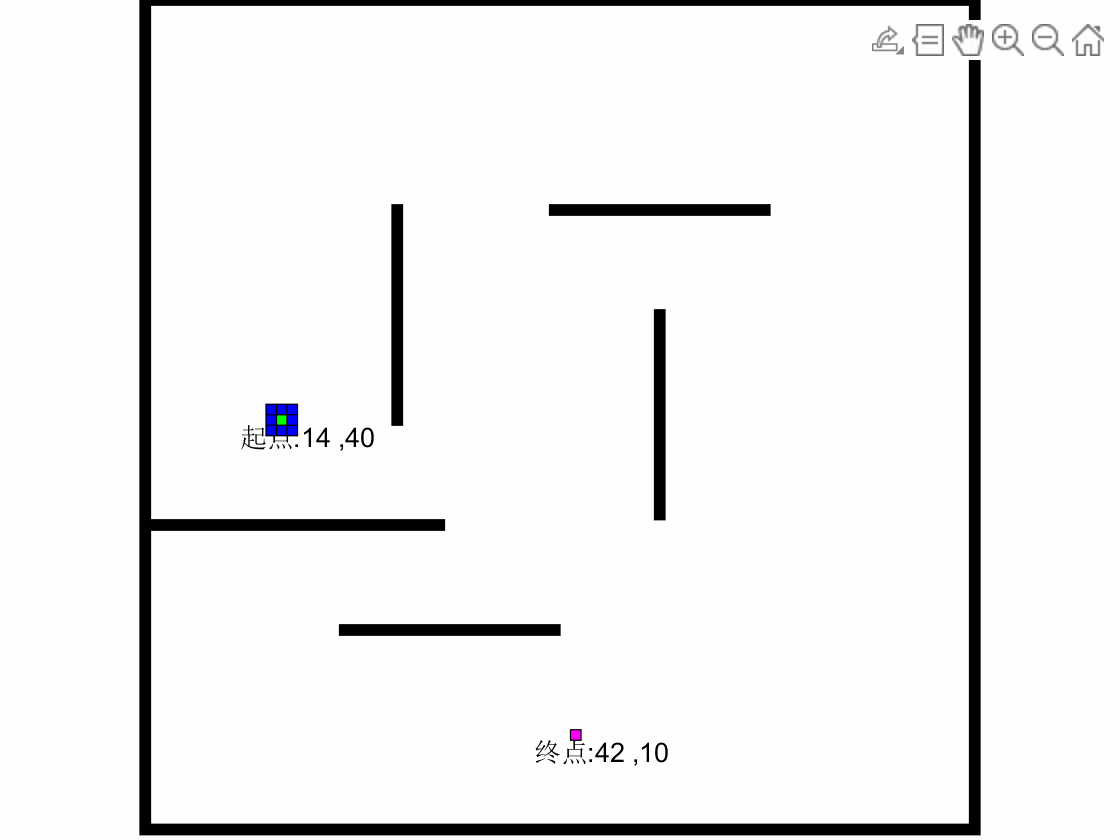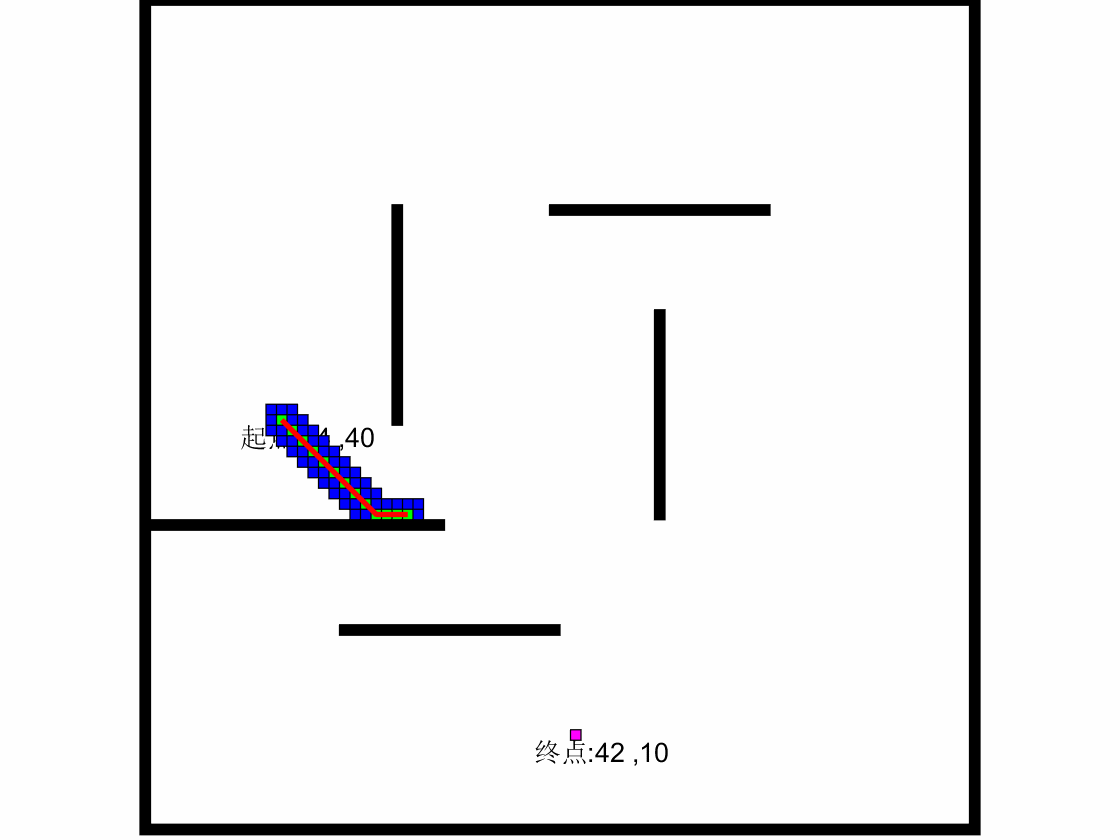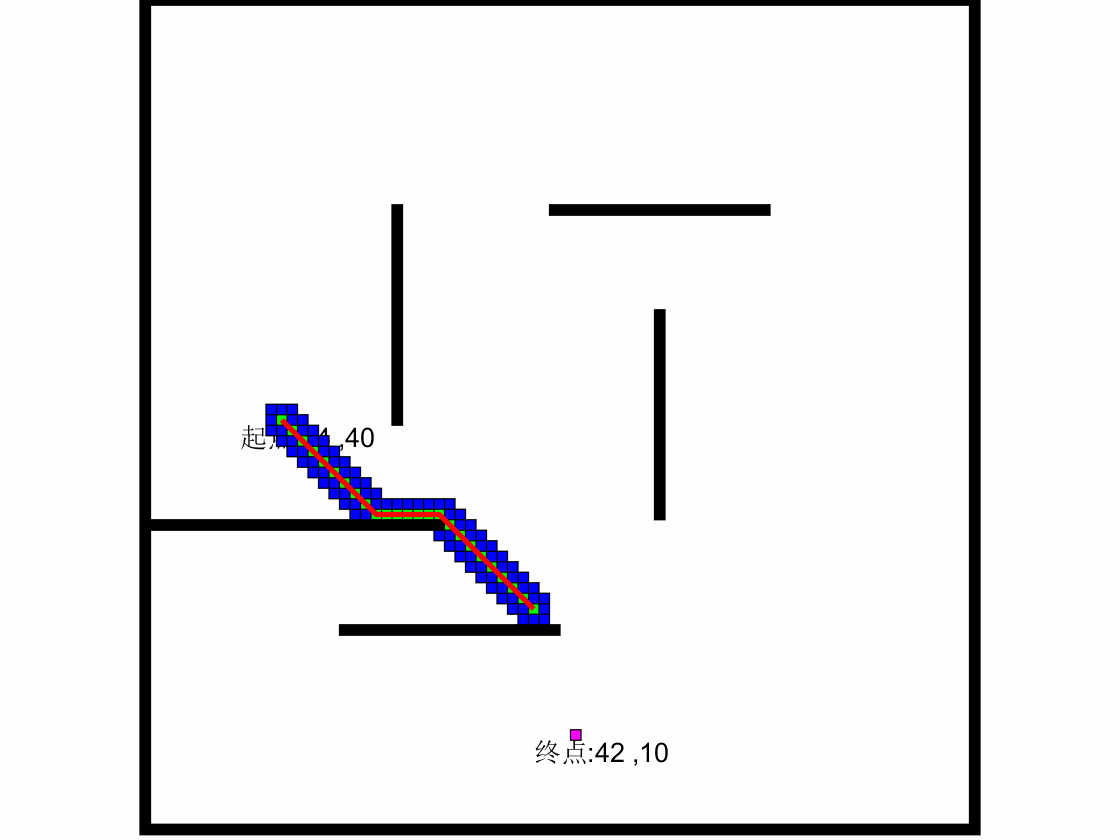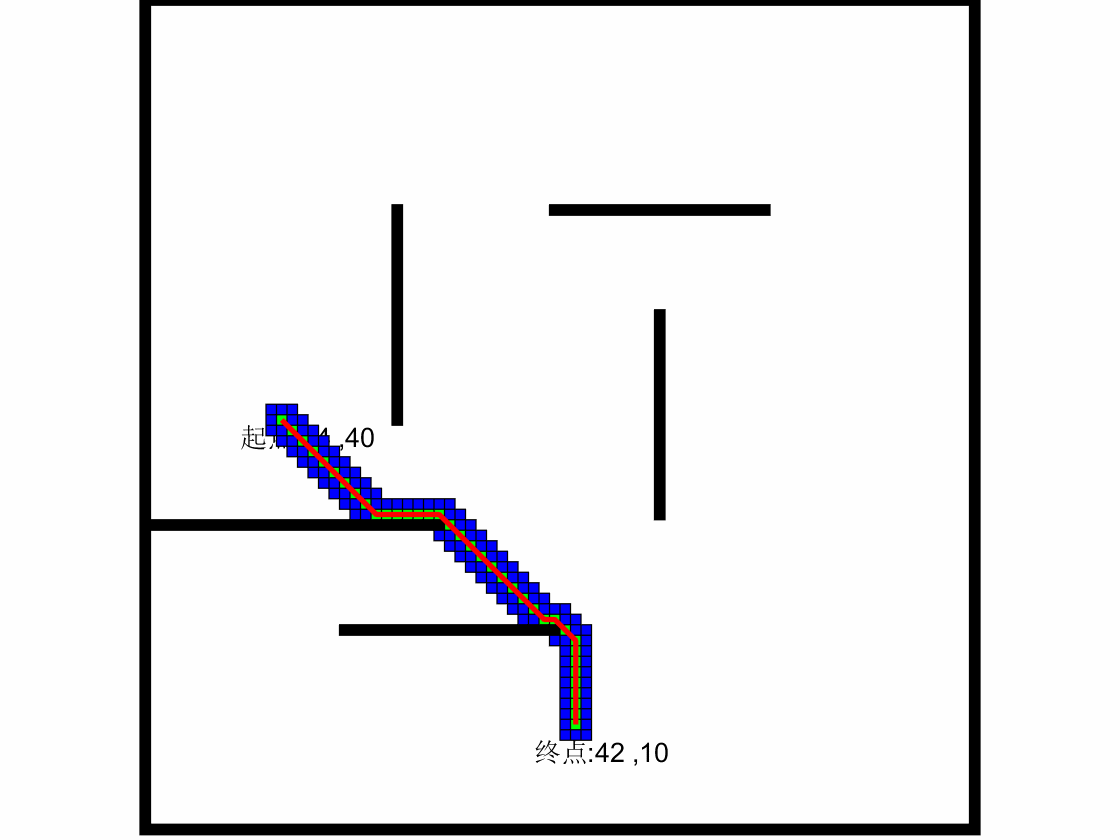
4.2.1 案例应用:迷宫最小步数
起点:1 1
终点:4 3
地图:0代表障碍物,1代表通道
1 1 0 1
1 1 1 1
1 1 0 1
1 0 1 1
1 1 1 0
求到达目标点的最短路径
完整C++代码
#include<iostream>
#include<vector>
#include<math.h>
using namespace std;
int start_x,start_y,end_x,end_y,width,height,step=0,min_step=9999;
int map[100][100],mark[100][100];
int direction[4][2]={{1,0},{0,-1},{-1,0},{0,1}};
/*
5 4
1 1 4 3
1 1 0 1
1 1 1 1
1 1 0 1
1 0 1 1
1 1 1 0
*/
struct Point
{
int x;
int y;
int g;
int h;
int f;
int father;
};
struct Map
{
int Info[100][100];
int RangexMin;
int RangexMax;
int RangeyMin;
int RangeyMax;
int startx;
int starty;
int endx;
int endy;
};
void mapInit(Map &map)
{
map.RangexMin =0;map.RangeyMin =0;
scanf("%d%d",&map.RangexMax,&map.RangeyMax);
scanf("%d%d%d%d",&map.startx,&map.starty,&map.endx,&map.endy);
for(int i=1; i<=map.RangexMax; i++)
for(int j =1; j<=map.RangeyMax; j++)
scanf("%d",&map.Info[i][j]);
}
void findOptimalPoint(Point &optimalPoint, vector<Point> &Openlist, vector<Point> &Closedlist)
{
vector<Point>::iterator Miniter;
int Minf = 9999;
for(auto iter = Openlist.begin();iter!=Openlist.end();iter++)
{
if(iter->f < Minf)
{
Minf = iter->f;
Miniter = iter;
}
}
optimalPoint = *Miniter;
Openlist.erase(Miniter);
Closedlist.push_back(optimalPoint);
}
void findNeighborPoint(Point &CurrentPoint, vector<Point> &NeighborPoint, vector<Point> &Closedlist, Map &map)
{
for(int i=0; i<4; i++)
{
int okFlag = 1;
int temp_x = CurrentPoint.x+direction[i][0];
int temp_y = CurrentPoint.y+direction[i][1];
if (temp_x <map.RangexMin || temp_y < map.RangeyMin || temp_x>map.RangexMax || temp_y>map.RangeyMax)
okFlag = 0;
if (map.Info[temp_x][temp_y] == 0)
okFlag = 0;
for (auto iter = Closedlist.begin();iter!=Closedlist.end();iter++)
{
if (iter->x == temp_x && iter->y == temp_y)
{
okFlag = 0;
}
}
if (okFlag == 1)
{
Point neighborPoint;
neighborPoint.x = temp_x; neighborPoint.y = temp_y;
NeighborPoint.push_back(neighborPoint);
}
}
}
bool Astar(Map &map)
{
vector<Point> Openlist;
vector<Point> Closedlist;
Point start,end;
start.x = map.startx;
start.y = map.starty;
end.x = map.endx;
end.y = map.endy;
start.g = 0;
start.h = abs(end.x -start.x) +abs(end.y -start.y);
start.f = start.g+start.h;
start.father = -1;
Openlist.push_back(start);
while(~Openlist.empty())
{
//查找开放列表中最优节点,删除开放列表中该节点,并将其插入关闭列表
Point optimalPoint;
findOptimalPoint(optimalPoint, Openlist,Closedlist);
//如果该点为目标点,退出
if (optimalPoint.x == map.endx && optimalPoint.y == map.endy)
{
cout << "找到啦"<<endl;
int i = Closedlist.size()-1;
while(i>=0)
{
map.Info[Closedlist[i].x][Closedlist[i].y] = 6;
i = Closedlist[i].father;
}
return 1;
}
//探索有效最优节点的邻居
vector<Point> NeighborPoint;
findNeighborPoint(optimalPoint,NeighborPoint,Closedlist,map);
//更新邻居节点数据
for(int i=0; i<NeighborPoint.size();i++)
{
Point point = NeighborPoint[i];
int g = optimalPoint.g + abs(optimalPoint.x-point.x)+abs(optimalPoint.y-point.y);
int h = abs(map.endx-point.x)+abs(map.endy-point.y);
int f = g+h;
//查看是否位于开放列表
bool inOpenlist;
for(auto iter=Openlist.begin();iter!=Openlist.end();iter++)
{
if(point.x == iter->x && point.y == iter->y)
{//在开放列表
if (iter->f > f)
{
iter->f = f;
iter->g = g;
iter->h = h;
iter->father = Closedlist.size()-1;
inOpenlist = 0;
}
}
}
if(~inOpenlist)
{//不在开放列表
point.f = f;
point.g = g;
point.h = h;
point.father = Closedlist.size()-1;
Openlist.push_back(point);
}
}
}
return 0;
}
int main()
{
Map map;
mapInit(map);
bool flag = Astar(map);
if (flag == 1)
{
for(int i=1;i<=map.RangexMax;i++)
{
for(int j=1;j<=map.RangeyMax;j++)
{
cout<<map.Info[i][j]<<" ";
}
cout<<endl;
}
}
else
cout <<"Not OK"<<endl;
return 0;
}
5. 结论
A算法是一种功能强大的路径规划和图搜索工具,适用于多个领域。虽然它的原理相对简单,但在实际应用中通常需要与数据结构和问题领域相结合以获得最佳性能。希望本文有助于您更深入地理解A算法,并在您的项目中应用它。
参考文献:
- Hart, P. E., Nilsson, N. J., & Raphael, B. (1968). A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Science and Cybernetics, 4(2), 100-107.
