二叉树遍历的概念：

二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次。

1、前序遍历

    先输出当前结点的数据，再依次遍历输出左结点和右结点

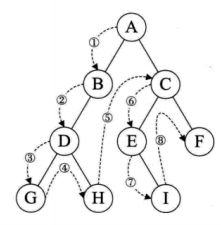
如下图二叉树分析：

   遍历过程   A  (B,C)              (括号里代表该节点的子节点，  每次把遍历节点放再子节点的左右节点之前)

                    A   B (D)   C (E)   F

                    A  B   D  G  H  C  E(I)  F

    最终结果   A B D G H C E I F

2，中序遍历

    先遍历输出左结点，再输出当前结点的数据，再遍历输出右结点

   遍历过程   A (B,C)               (括号里代表该节点的子节点，  每次把遍历节点放再子节点的左右节点中间)

                    B(D)  A  C(E,F)

                    D(G,H)  B  A C(E,F)

                    G D H  B  A C(E,F)

                    G D H  B  A  E(I)  C F

                    G D H  B  A  E  I  C  F

最终结果：   GＤH B A E I C F

3，后序遍历

 先遍历输出左结点，再遍历输出右结点，最后输出当前结点的数据

   遍历过程   A (B,C)                    (括号里代表该节点的子节点，  每次把遍历节点放再子节点的左右节点之后)

                    B(D)  C(E,F)  A

                    D(G,H)  B   C(E,F)  A

                    G H D B C(E,F)  A

                    G H D B E（I） F C  A

                    G H D B I E F C  A

最终结果： G H D B I E F C A 

       一般的树来说是一对多的关系，使用顺序结构存储起来比较困难，但是二叉树是一种特殊的树，每个结点最多有两个子节点，并且子节点有左右之分，并且兄弟，父亲，孩子可以很方便的通过编号得到，所以我们使用顺序存储结构使用二叉树的存储。

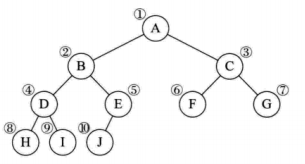
如下二叉树

顺序存储：   （顺序存储一般只用于完全二叉树）

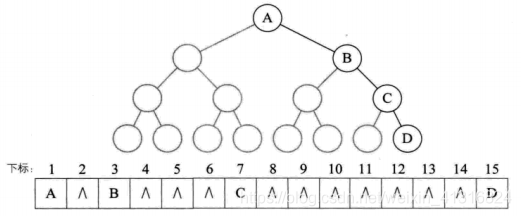
非完全二叉树使用顺序存储时需要空出很多内存

以该二叉树为例： 

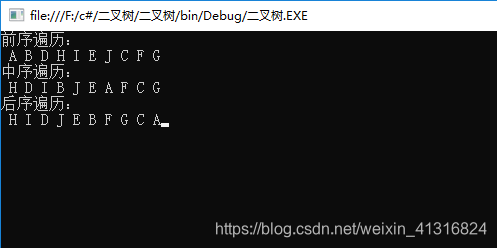
代码实现二叉树的存储及遍历：

    class BTree<T>
    {
        private T[] data;
        private int count = 0;
        /// <summary>
        /// 
        /// </summary>
        /// <param name="capacity">数组容量</param>
        public BTree(int capacity)
        {
            data = new T[capacity];
        }

        public void AddItem(T item)
        {
            if (data.Length <= count)
            {
                return;
            }
            data[count] = item;
            count++;
        }

        // 前序遍历
        public void PreorderTraversal()
        {
            PreorderTraversal(0);
        }

        private void PreorderTraversal(int index)
        {
            if (index >= data.Length) return;
            Console.Write(" " + data[index]);
            int num = index + 1;
            int left = 2 * num;
            int right = 2 * num + 1;
            PreorderTraversal(left - 1);
            PreorderTraversal(right - 1);
        }


        // 中序遍历
        public void SequentialTraversal()
        {
            SequentialTraversal(0);
        }

        private void SequentialTraversal(int index)
        {
            if (index >= data.Length) return;
            int num = index + 1;
            int left = num * 2;
            int right = num * 2 + 1;

            SequentialTraversal(left - 1);
            Console.Write(" " + data[index]);
            SequentialTraversal(right - 1);

        }

        // 后续遍历
        public void PostOrderTraversal()
        {
            PostOrderTraversal(0);
        }

        private void PostOrderTraversal(int index)
        {
            if (index >= data.Length) return;
            int num = index + 1;
            int left = num * 2;
            int right = num * 2 + 1;

            PostOrderTraversal(left - 1);
            PostOrderTraversal(right - 1);
            Console.Write(" " + data[index]);
        }
    }


    class Program
    {
        static void Main(string[] args)
        {
            char[] data = { 'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J' };

            BTree<char> tree = new BTree<char>(data.Length);
            for (int i = 0; i < data.Length; i++)
            {
                tree.AddItem(data[i]);
            }

            Console.WriteLine("前序遍历：");
            tree.PreorderTraversal();
            Console.WriteLine();
            Console.WriteLine("中序遍历：");
            tree.SequentialTraversal();
            Console.WriteLine();
            Console.WriteLine("后序遍历：");
            tree.PostOrderTraversal();
            Console.ReadKey();
        }
    }