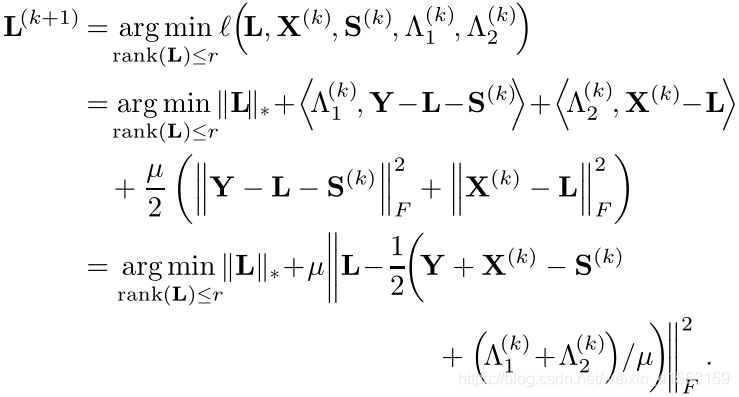引言

HSI去噪方法：HSSNR、MWF、high-order rank-1 tensor decomposition等。

尽管TV正则化方法在图像处理方面表现良好，但在去除脉冲噪声方面仍面临一些问题。值得注意的是，TV正则化会对未被脉冲破坏的像素值产生负面影响。

最著名的传统低秩方法之一是主成分分析，它使用正交变换将高光谱图像转换成一组称为主成分的线性不相关变量。不幸的是，这种经典方法有两个主要缺点。一是对离群值(outliers)敏感；然而，HSI经常被异常值所污染，例如条纹、死线、脉冲噪声等。其次，它主要利用光谱波段之间的相关性，忽略了局部邻域像素的空间分段平滑性。RPCA模型解决了第一个问题。

TV Model For HSI Restoration

退化模型(省略加粗)：$Y=X+S+N$，$Y\in {\mathbb{R}}^{MN\times p}$，三维情形：$u=f+s+\mathcal{N}$

MAP Restoration Model：HSI恢复模型可以描述为以下约束最小二乘问题$$\hat{\mathbf{X}}=\underset{\mathbf{X}\in {\mathbb{R}}^{m\times n}}{\mathrm{argmin}}\left\{\Vert \mathbf{Y}-\mathbf{X}{\Vert }_F^2+\tau R(\mathbf{X})\right\}$$

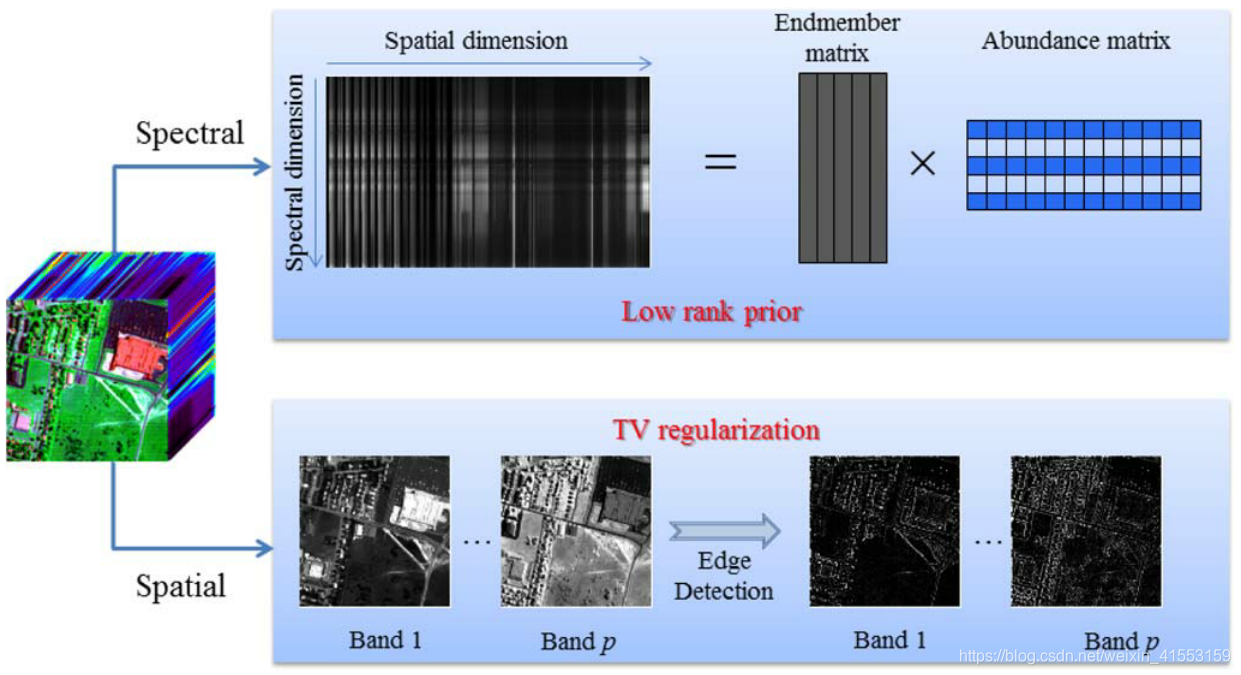
TV-Based HSI Restoration：对于尺寸为$M\times N$的灰度图像$x$，各向异性TV范数定义如下 ∥ x ∥ T V = ∑ i = 1 M − 1 ∑ j = 1 N − 1 { ∣ x i , j − x i + 1 , j ∣ + ∣ x i , j − x i , j + 1 ∣ } + ∑ i = 1 M − 1 ∣ x i , N − x i + 1 , N ∣ + ∑ j = 1 N − 1 ∣ x M , j − x M , j + 1 ∣ \begin{aligned} \|x\|_{\mathrm{TV}}=& \sum_{i=1}^{M-1} \sum_{j=1}^{N-1}\left\{\left|x_{i, j}-x_{i+1, j}\right|+\left|x_{i, j}-x_{i, j+1}\right|\right\} \\ &+\sum_{i=1}^{M-1}\left|x_{i, N}-x_{i+1, N}\right|+\sum_{j=1}^{N-1}\left|x_{M, j}-x_{M, j+1}\right| \end{aligned} ∥x∥TV​=​i=1∑M−1​j=1∑N−1​{∣xi,j​−xi+1,j​∣+∣xi,j​−xi,j+1​∣}+i=1∑M−1​∣xi,N​−xi+1,N​∣+j=1∑N−1​∣xM,j​−xM,j+1​∣​

简单的逐波段HSI TV标准定义如下$$\Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}=\sum _{j=1}^p{\Vert \mathcal{F}{\mathbf{X}}_j\Vert }_{\mathrm{T}\mathrm{V}}$$

其中${\mathbf{X}}_j$表示HSI的第$j$个波段向量，$\mathcal{F}:{\mathbb{R}}^{MN}\to {\mathbb{R}}^{M\times N}$，于是HSI恢复模型可以写成如下形式$$\hat{\mathbf{X}}=\underset{\mathbf{X}\in {\mathbb{R}}^{m\times n}}{\mathrm{argmin}}\left\{\Vert \mathbf{Y}-\mathbf{X}{\Vert }_F^2+\tau \Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}\right\}$$

对于一个HSI，它经常被混合噪声破坏，包括高斯噪声和稀疏噪声。在这种情况下，将数据保真度项强加于所有空间是不合适的。如果稀疏噪声候选集用$\Omega$表示，则基于TV的HSI恢复模型可以重写如下$$\hat{\mathbf{X}}=\underset{\mathbf{X}\in {\mathbb{R}}^{m\times n}}{\mathrm{argmin}}\left\{\Vert P_{{\Omega }^T}(\mathbf{Y}-\mathbf{X}){\Vert }_F^2+\tau \Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}\right\}$$

其中${\Omega }^T$为$\Omega$的补空间，$P_{{\Omega }^T}$is the orthogonal projector onto the span of the matrices vanishing in $\Omega$(没看懂).

如果稀疏噪声已知，则 $\hat{\mathbf{X}}=\underset{\mathbf{X}\in {\mathbb{R}}^{m\times n}}{\mathrm{argmin}}\left\{\Vert \mathbf{Y}-\mathbf{X}-\mathbf{S}{\Vert }_F^2+\tau \Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}\right\}$

通过仔细选择正则化参数$\tau$，上式转化为有约束的TV模型$$\hat{\mathbf{X}}=\underset{\mathbf{X}\in {\mathbb{R}}^{m\times n}}{\mathrm{argmin}}\Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}\text{ s.t. }\Vert \mathbf{Y}-\mathbf{X}-\mathbf{S}{\Vert }_F^2\le \epsilon$$

其中$\epsilon$代表高斯噪声的噪声水平。

LRTV For HSI Restoration

左上角是否反了？因为$X\in {\mathbb{R}}^{MN\times p}$.

Low-Rank Matrix Factorization-Based HSI Restoration

从线性光谱混合模型的角度来看，每个光谱特征(X的行)可以由少量纯光谱端元的线性组合来表示，这启发我们使用低秩矩阵分解来对HSI降级建模$$Y=UV+S+N$$其中$U\in {\mathbb{R}}^{m\times r}$为端元矩阵或字典，$V\in {\mathbb{R}}^{r\times n}$为abundance或系数矩阵，$UV$为原始干净图像的低秩矩阵分解，$r$为端元(endmembers)的个数。

在低秩矩阵分解模型中，我们假设$U$是一个随机字典。矩阵$V$的系数值也假设是随机分布的。这些假设已被概率矩阵分解和贝叶斯RPCA采纳。

我们假设$U$和$V$的每个元素从高斯分布采样，稀疏误差S从拉普拉斯分布采样，噪声G服从高斯分布。从概率的角度来看，我们有以下几点$$\begin{array}{rl}{\mathbf{U}}_{ij}& \sim \mathcal{N}\left(0,{\lambda }_u^{-1}\right)\\ {\mathbf{V}}_{ij}& \sim \mathcal{N}\left(0,{\lambda }_v^{-1}\right)\\ {\mathbf{S}}_{ij}& \sim \mathcal{L}\left(0,{\lambda }_s^{-1}\right)\\ {\mathbf{G}}_{ij}& \sim \mathcal{N}\left(0,{\lambda }_g^{-1}\right)\end{array}$$

通过将$U,V,S$视为模型参数，${\lambda }_u,{\lambda }_v,{\lambda }_s,{\lambda }_g$为具有固定值的超参数，我们使用贝叶斯估计去寻找$U,V,S$. 根据贝叶斯法则，我们有以下MAP公式(后3个正比式可由https://zhuanlan.zhihu.com/p/75380549推得，第一个正比式不知道怎么推)
$$\begin{gathered} p\left(\mathbf{U},\mathbf{V},\mathbf{S}\mid \mathbf{Y},{\lambda }_u,{\lambda }_v,{\lambda }_s,{\lambda }_g\right) \\ \propto p\left(\mathbf{Y}\mid \mathbf{U},\mathbf{V},\mathbf{S},{\lambda }_g\right)p\left(\mathbf{U}\mid {\lambda }_u\right)p\left(\mathbf{V}\mid {\lambda }_v\right)p\left(\mathbf{S}\mid {\lambda }_s\right). \end{gathered}$$

因此(没看懂)$$\begin{gathered} \log p\left(\mathbf{U},\mathbf{V},\mathbf{S}\mid \mathbf{Y},{\lambda }_u,{\lambda }_v,{\lambda }_s,{\lambda }_g\right)=-\frac{{\lambda }_g}{2}\Vert \mathbf{Y}-\mathbf{U}\mathbf{V}-\mathbf{S}{\Vert }_F^2 \\ -{\lambda }_s\Vert \mathbf{S}{\Vert }_1-\frac{{\lambda }_u}{2}\Vert \mathbf{U}{\Vert }_F^2-\frac{{\lambda }_v}{2}\Vert \mathbf{V}{\Vert }_F^2-C \end{gathered}$$

其中$C$为独立于$U,V,S$的常数项，令$\lambda ={\lambda }_s/{\lambda }_g$，${\lambda }_u^{\prime }={\lambda }_u/{\lambda }_g$，${\lambda }_v^{\prime }={\lambda }_v/{\lambda }_g$，则MAP相当于下面的恢复模型$$\underset{\mathbf{U},\mathbf{V},\mathbf{S}}{\min }\frac{1}{2}\Vert \mathbf{Y}-\mathbf{U}\mathbf{V}-\mathbf{S}{\Vert }_F^2+\lambda \Vert \mathbf{S}{\Vert }_1+\frac{{\lambda }_u^{\prime }}{2}\Vert \mathbf{U}{\Vert }_F^2+\frac{{\lambda }_v^{\prime }}{2}\Vert \mathbf{V}{\Vert }_F^2(1)$$

然后，我们可以进一步简化低秩矩阵分解模型(1)，并在特定条件下推导秩约束的RPCA模型。

引理1：对于任意的矩阵$X\in {\mathbb{R}}^{m\times n}$，有$$\Vert \mathbf{X}{\Vert }_{\ast }=\underset{\mathbf{U},\mathbf{V},\mathbf{X}=\mathbf{U}\mathbf{V}}{\min }\frac{1}{2}\left(\Vert \mathbf{U}{\Vert }_F^2+\Vert \mathbf{V}{\Vert }_F^2\right)$$如果 r a n k ( X ) = r ≤ m i n { m , n } rank(X)=r\leq min\{m,n\} rank(X)=r≤min{m,n}，那么上述最小值在因子(factor)分解$X=UV$时获得，其中$U\in {\mathbb{R}}^{m\times r}$，$V\in {\mathbb{R}}^{r\times n}$.

假设${\lambda }_u^{\prime }={\lambda }_v^{\prime }={\lambda }_2$，且秩的上界为$r$，于是由引理1可知$$\begin{array}{rl}\underset{\mathbf{U},\mathbf{V},\mathbf{S}}{\min }& \frac{1}{2}\Vert \mathbf{Y}-\mathbf{U}\mathbf{V}-\mathbf{S}{\Vert }_F^2+\lambda \Vert \mathbf{S}{\Vert }_1+\frac{{\lambda }_2}{2}\Vert \mathbf{U}{\Vert }_F^2+\frac{{\lambda }_2}{2}\Vert \mathbf{V}{\Vert }_F^2\\ & =\underset{\mathbf{U},\mathbf{V},\mathbf{S}}{\min }\frac{1}{2}\Vert \mathbf{Y}-\mathbf{U}\mathbf{V}-\mathbf{S}{\Vert }_F^2+\lambda \Vert \mathbf{S}{\Vert }_1+{\lambda }_2\left(\Vert \mathbf{U}\mathbf{V}{\Vert }_{\ast }\right)\\ & =\underset{\mathbf{X},\mathbf{S},\mathrm{rank}(\mathbf{X})\le r}{\min }\frac{1}{2}\Vert \mathbf{Y}-\mathbf{X}-\mathbf{S}{\Vert }_F^2+\lambda \Vert \mathbf{S}{\Vert }_1+{\lambda }_2\left(\Vert \mathbf{X}{\Vert }_{\ast }\right).\end{array}$$

从上式中，我们可以看到低秩矩阵分解恢复模型(1)是秩约束的RPCA模型的拉格朗日形式，如下所示$$\underset{\mathbf{X},\mathbf{S}\in {\mathbb{R}}^{m\times n}}{\min }\Vert \mathbf{X}{\Vert }_{\ast }+\lambda \Vert \mathbf{S}{\Vert }_1\text{ s.t. }\Vert \mathbf{Y}-\mathbf{X}-\mathbf{S}{\Vert }_F^2\le \epsilon ,\mathrm{rank}(\mathbf{X})\le r(2)$$

其中$\epsilon$代表噪声方差。由于包含秩约束，秩约束RPCA模型(2)是非凸的，但是它可以通过基于ALM的方法来求解。把模型(2)称为低秩矩阵分解。

The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices

LRTV for HSI Restoration

在稀疏噪声的位置随机分布的情况下，这种低秩矩阵分解模型只能从观察到的图像中分离稀疏噪声。也就是说，对于HSI数据，如果条纹位于所有波段中的相同位置，低秩矩阵分解模型(2)将无法检测到这些条纹，并将稀疏噪声视为低秩分量。而TV模型忽略光谱相似性，并且需要预先定义稀疏噪声的值或位置。我们可以执行以下LRTV恢复模型：$$\begin{gathered} \underset{\mathbf{X},\mathbf{S}\in {\mathbb{R}}^{m\times n}}{\min }\Vert \mathbf{X}{\Vert }_{\ast }+\tau \Vert \mathbf{X}{\Vert }_{HTV}+\lambda \Vert \mathbf{S}{\Vert }_1 \\ \text{s.t. }\Vert \mathbf{Y}-\mathbf{X}-\mathbf{S}{\Vert }_F^2\le \epsilon ,\mathrm{rank}(\mathbf{X})\le r(3) \end{gathered}$$

其中$\tau$是用于控制核范数和TV范数之间的折衷的参数，$\lambda$是用于限制稀疏噪声的稀疏性的参数。

Optimization Procedure（比较难）

本文采用了ALM方法解决优化问题(3)。将(3)转化为$$\begin{array}{rl}& \underset{\mathbf{L},\mathbf{X},\mathbf{S}\in {\mathbb{R}}^{m\times n}}{\min }\Vert \mathbf{L}{\Vert }_{\ast }+\tau \Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}+\lambda \Vert \mathbf{S}{\Vert }_1\\ & \text{ s.t. }\Vert \mathbf{Y}-\mathbf{L}-\mathbf{S}{\Vert }_F^2\le \epsilon ,\mathrm{rank}(\mathbf{L})\le r,\mathbf{L}=\mathbf{X}\end{array}$$

这个问题可以通过ALM方法来解决，该方法最小化了以下增广拉格朗日函数$$\begin{array}{rl}\min \ell \left(\mathbf{L},\mathbf{X},\mathbf{S},{\Lambda }_1,{\Lambda }_2\right)=& \underset{\mathbf{X},\mathbf{S},\mathbf{L},{\Lambda }_1,{\Lambda }_2}{\min }\Vert \mathbf{L}{\Vert }_{\ast }+\tau \Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}+\lambda \Vert \mathbf{S}{\Vert }_1\\ & +⟨{\Lambda }_1,\mathbf{Y}-\mathbf{L}-\mathbf{S}⟩+⟨{\Lambda }_2,\mathbf{X}-\mathbf{L}⟩\\ & +\frac{\mu }{2}\left(\Vert \mathbf{Y}-\mathbf{L}-\mathbf{S}{\Vert }_F^2+\Vert \mathbf{X}-\mathbf{L}{\Vert }_F^2\right)\\ \text{ s.t. }& \mathrm{rank}(\mathbf{L})\le r\end{array}$$

其中$\mu$是惩罚参数，${\Lambda }_1$和${\Lambda }_2$是拉格朗日乘子(multipliers)。在一个变量上迭代优化增广拉格朗日函数，同时固定其他变量。具体来说，在第$k+1$次迭代中，我们更新变量如下$$\begin{array}{rl}{\mathbf{L}}^{(k+1)}& =\underset{rank\left(\mathbf{L}\right)⩽r}{\mathrm{argmin}}\ell \left(\mathbf{L},{\mathbf{X}}^{(k)},{\mathbf{S}}^{(k)},{\Lambda }_1^{(k)},{\Lambda }_2^{(k)}\right)(a)\\ {\mathbf{X}}^{(k+1)}& =\underset{\mathbf{X}}{\mathrm{argmin}}\ell \left({\mathbf{L}}^{(k+1)},\mathbf{X},{\mathbf{S}}^{(k)},{\Lambda }_1^{(k)},{\Lambda }_2^{(k)}\right)(b)\\ {\mathbf{S}}^{(k+1)}& =\underset{\mathbf{S}}{\mathrm{argmin}}\ell \left({\mathbf{L}}^{(k+1)},{\mathbf{X}}^{(k+1)},\mathbf{S},{\Lambda }_1^{(k)},{\Lambda }_2^{(k)}\right)(c)\\ {\Lambda }_1^{(k+1)}& ={\Lambda }_1^{(k)}+\mu \left(\mathbf{Y}-{\mathbf{L}}^{(k+1)}-{\mathbf{S}}^{(k+1)}\right)(d)\\ {\Lambda }_2^{(k+1)}& ={\Lambda }_2^{(k)}+\mu \left({\mathbf{X}}^{(k+1)}-{\mathbf{L}}^{(k+1)}\right)(e)\end{array}$$

优化问题现在被分成三个主要的子问题，如$(a)-(c)$所示。对于$(a)$，我们可以推导出(最后一个等式没看懂)

更新$\mathbf{L}$的步骤可以用下面的引理2来求解。

引理2：矩阵$\mathbf{W}\in {\mathbb{R}}^{MN\times p}$的秩$r$奇异值分解为 W = U E r V ∗ , E r = diag ⁡ ( { σ i } 1 ≤ i ≤ r ) \mathbf{W}=U E_{r} V^{*}, E_{r}=\operatorname{diag}\left(\left\{\sigma_{i}\right\}_{1 \leq i \leq r}\right) W=UEr​V∗,Er​=diag({σi​}1≤i≤r​)

奇异值收缩算子满足$$D_{\delta }(\mathbf{W})=\underset{\mathrm{rank}(\mathbf{L})\le r}{\mathrm{argmin}}\delta \Vert \mathbf{L}{\Vert }_{\ast }+\frac{1}{2}\Vert \mathbf{L}-\mathbf{W}{\Vert }_F^2$$

其中 D δ ( W ) = U D δ ( E r ) V ∗ , D δ ( E r ) = diag ⁡ { max ⁡ ( ( σ i − δ ) , 0 ) } D_{\delta}(\mathbf{W})=U D_{\delta}\left(E_{r}\right) V^{*}, D_{\delta}\left(E_{r}\right)=\operatorname{diag}\left\{\max \left(\left(\sigma_{i}-\delta\right), 0\right)\right\} Dδ​(W)=UDδ​(Er​)V∗,Dδ​(Er​)=diag{max((σi​−δ),0)}

通过使用引理2，我们可以容易地获得以下优化结果$${\mathbf{L}}^{(k+1)}=D_{\frac{1}{(2\mu )}}\left(\frac{1}{2}\left(\mathbf{Y}+{\mathbf{X}}^{(k)}-{\mathbf{S}}^{(k)}+\left({\Lambda }_1^{(k)}+{\Lambda }_2^{(k)}\right)/\mu \right)\right)$$

对于子问题$(b)$，有$$\begin{array}{rl}{\mathbf{X}}^{(k+1)}=& \underset{\mathbf{X}}{\mathrm{argmin}}\ell \left({\mathbf{L}}^{(k+1)},\mathbf{X},{\mathbf{S}}^{(k)},{\Lambda }_1^{(k)},{\Lambda }_2^{(k)}\right)\\ =& \underset{\mathbf{X}}{\mathrm{argmin}}\tau \Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}+⟨{\Lambda }_2^{(k)},\mathbf{X}-{\mathbf{L}}^{(k+1)}⟩\\ & +\frac{\mu }{2}{\Vert \mathbf{X}-{\mathbf{L}}^{(k+1)}\Vert }_F^2\\ =& \arg \underset{\mathbf{X}}{\min }\tau \Vert \mathbf{X}{\Vert }_{\mathrm{H}\mathrm{T}\mathrm{V}}+\frac{\mu }{2}{\Vert \mathbf{X}-{\mathbf{L}}^{(k+1)}+\frac{{\Lambda }_2^{(k)}}{\mu }\Vert }_F^2\end{array}$$

我们定义$Q={\mathbf{L}}^{(k+1)}-\left({\Lambda }_2^{(k)}/\mu \right)$以及$Q=\left[Q_1,Q_2,\dots ,Q_p\right]\in {\mathbb{R}}^{MN\times p}$，上述优化可以分成$p$个子问题，每个子问题都要解决($\mathbf{H}{\mathbf{X}}_j$是什么？)$${\mathbf{X}}_j^{(k+1)}=\underset{{\mathbf{X}}_j}{\mathrm{argmin}}\frac{\tau }{\mu }{\Vert \mathbf{H}{\mathbf{X}}_j\Vert }_{\mathrm{T}\mathrm{V}}+\frac{1}{2}{\Vert {\mathbf{X}}_j-Q_j\Vert }^2$$

在本文中，我们使用快速基于梯度的算法(Ref：Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems)来求解上式。对于子问题$(c)$，有$$\begin{array}{rl}{\mathbf{S}}^{(k+1)}=& \underset{\mathbf{S}}{\mathrm{argmin}}\ell \left({\mathbf{L}}^{(k+1)},{\mathbf{X}}^{(k+1)},\mathbf{S},{\Lambda }_1^{(k)},{\Lambda }_2^{(k)}\right)\\ =& \underset{\mathbf{S}}{\mathrm{argmin}}\lambda \Vert \mathbf{S}{\Vert }_1+⟨{\Lambda }_1^{(k)},\mathbf{Y}-{\mathbf{L}}^{(k+1)}-\mathbf{S}⟩\\ & +\frac{\mu }{2}{\Vert \mathbf{Y}-{\mathbf{L}}^{(k+1)}-\mathbf{S}\Vert }_F^2\\ =& \underset{\mathbf{S}}{\mathrm{argmin}}\lambda \Vert \mathbf{S}{\Vert }_1+\frac{\mu }{2}{\Vert \mathbf{S}-\left(\mathbf{Y}-{\mathbf{L}}^{(k+1)}+\frac{{\Lambda }_1^{(k)}}{\mu }\right)\Vert }^2(4)\end{array}$$

通过引入下面的软阈值(收缩)算子$${\Re }_{\Delta }(x)=\{\begin{array}{ll}x-\Delta ,& \text{ if }x>\Delta \\ x+\Delta ,& \text{ if }x<-\Delta \\ 0,& \text{ otherwise }\end{array}$$

其中$x\in \mathbb{R},\Delta >0$，(4)的优化可以表示如下$${\mathbf{S}}^{(k+1)}={\Re }_{\frac{\lambda }{\mu }}\left(\mathbf{Y}-{\mathbf{L}}^{(k+1)}+\frac{{\Lambda }_1^{(k)}}{\mu }\right)$$

总结前面的描述，我们得到了一个增广拉格朗日交替方向法来求解LRTV模型，算法如下：

(22)即为(a)…(e)那里。

Robust recovery of subspace structures by low-rank representation
Constrained Optimization and Lagrange Multiplier Methods

Parameter Determination

$\lambda =1/\sqrt{MN}$，${\epsilon }_1={\epsilon }_2=10^{-8}$，借助于[Ref：Hyperspectral subspace identification]提出的称为HySime的HSI子空间识别方法来估计端元的数量$r$，$\tau =0.01$.

实验

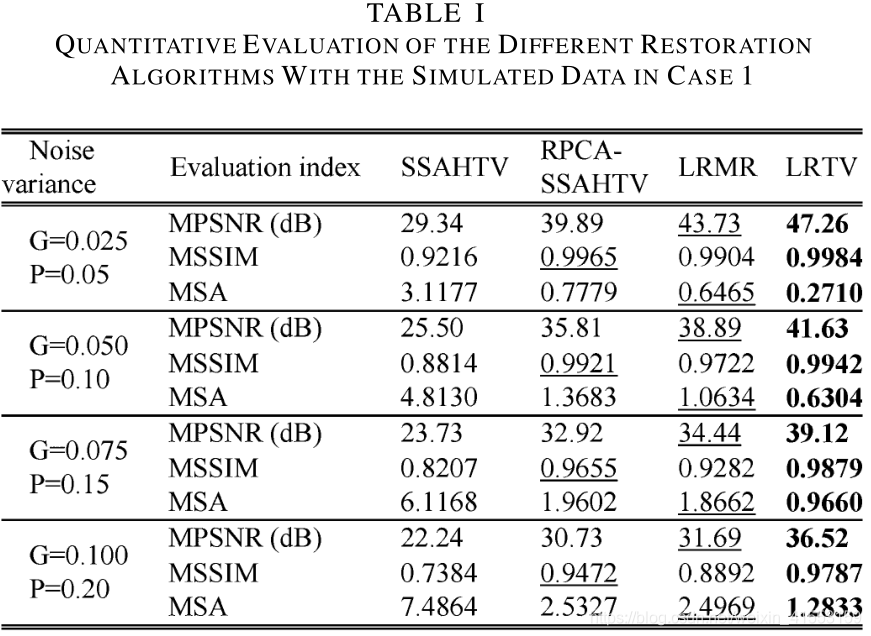
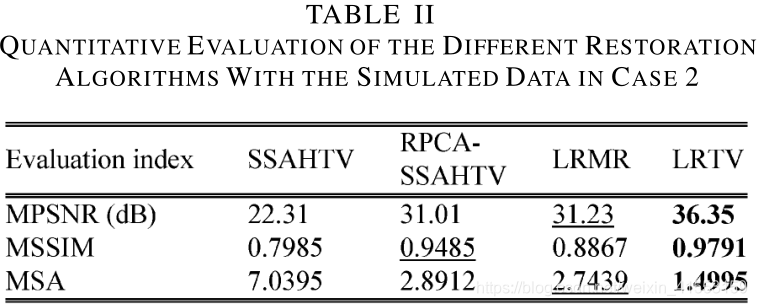
对比：SSAHTV，LRMR
模拟实验：Indian Pines(GT，145×145×224)
https://engineering.purdue.edu/~biehl/MultiSpec/hyperspectral.html
http://speclab.cr.usgs.gov/spectral.lib

真实实验：

• HYDICE urban data set, http://www.tec.army.mil/hypercube, 200×200×210
• Indian Pines data set, 145×145×220
• EO-1 Hyperion data set, http://www.gscloud.cn/, 200×200×166

改进之处：尽管LRTV性能良好，但它仍有进一步改进的空间。在实验中，我们将相同的参数值添加到HSI的所有波段。然而，正如SSAHTV中所介绍的，不同波段的噪声强度应该是不同的。也就是说，结合低秩约束的噪声调整TV正则化将在未来被研究。

源代码

1