一、什么是激活函数?
一个神经元会同时接收多个信号,然后将这些信号乘以一定权重求和,再用函数处理后再输出新的信号。对神经元的输入进行处理,以获得输出的函数称为激活函数。
二、为什么要用激活函数?
- 激活函数对模型学习、理解非常复杂和非线性的函数具有重要作用。
- 激活函数可以引入非线性因素。如果不使用激活函数,则输出信号仅是一个简单的线性函数。线性函数一个一级多项式,线性方程的复杂度有限,从数据中学习复杂函数映射的能力很小。没有激活函数,神经网络将无法学习和模拟其他复杂类型的数据,例如图像、视频、音频、语音等。
- 激活函数可以把当前特征空间通过一定的线性映射转换到另一个空间,让数据能够更好的被分类。
三、为什么激活函数需要非线性函数?
- 假若网络中全部是线性部件,那么线性的组合还是线性,与单独一个线性分类器无异。这样就做不到用非线性来逼近任意函数。
- 使用非线性激活函数 ,以便使网络更加强大,增加它的能力,使它可以学习复杂的事物,复杂的表单数据,以及表示输入输出之间非线性的复杂的任意函数映射。使用非线性激活函数,能够从输入输出之间生成非线性映射。
四、常见的激活函数
1. sigmoid函数
sigmoid函数是最常用的连续、平滑的激励函数,也被称作逻辑函数(Logistic函数)。用于隐层神经元输出,可以将一个实数映射到(0,1)的区间,用来做二分类。
a. 函数定义: f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1,值域: ( 0 , 1 ) (0,1) (0,1)。
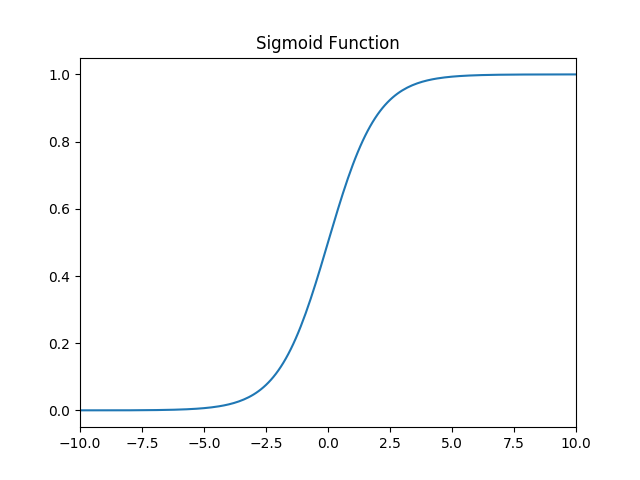
b. 函数图像:
c. 导数:: f ′ ( x ) = 1 1 + e − x ( 1 − 1 1 + e − x ) = f ( x ) ( 1 − f ( x ) ) f^{'}(x)=\frac{1}{1+e^{-x}}\left( 1- \frac{1}{1+e^{-x}} \right)=f(x)(1-f(x)) f′(x)=1+e−x1(1−1+e−x1)=f(x)(1−f(x))
d. 特点:当 x = 10 x=10 x=10,或 x = − 10 x=-10 x=−10, f ′ ( x ) ≈ 0 f^{'}(x) \approx0 f′(x)