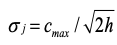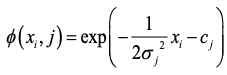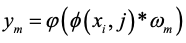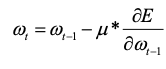文章目录
一、理论基础
径向基神经网络(Radial Basis Function Neural Network,简称RBFNN)是一种具有较强映射功能的三层前向网络,其原理与反向传播神经网络(BPNN)较为接近,最主要的特征为以径向基函数作为隐含层激活函数,数据从输入层传入隐含层后,通过径向基函数对其进行非线性映射,然后经过线性计算传递至输出层进行输出。
反向传播神经网络(BPNN)原理参考:
反向传播神经网络(BPNN)的实现(Python,附源码及数据集)
1、径向基神经网络结构
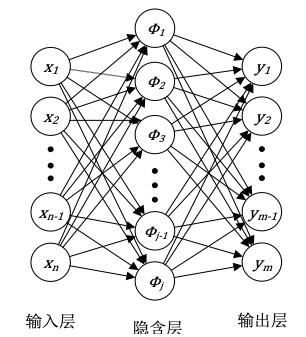
径向基神经网络的结构图如下图所示:
2、前向传播过程
径向基神经网络的前向传播过程类似于无监督学习,首先通过使用聚类算法如K-means对数据进行聚类,将聚类生成的中心点作为隐含层径向基函数的中心点,其中径向基函数一般选用高斯函数,然后利用中心点信息计算得出径向基函数的宽度向量,宽度向量的计算公式如下:
其中c_max为中心点之间的最大距离,h为节点数。
之后输入数据分别经过隐含层、输出层进行相关计算,输入样本x_i在隐含层的第j个节点的输出由以下公式计算得出:
其中c_j与σ_j分别为隐含层第j个节点的中心点与宽度向量,除上述方法外,还可直接随机生成隐含层的中心点与宽度向量。
输入样本x_i在输出层的第m个节点的输出由以下公式计算得出:
其中ω_m为该节点的权值,φ为激活函数。
激活函数原理参考:
神经网络基础知识之激活函数
3、反向传播过程
径向基神经网络的反向传播过程类似于监督学习,主要是对网络隐含层的中心点、宽度向量以及输出层的权值、阈值进行不断修正的过程,这一过程主要通过损失函数计算出每个参数的梯度值,然后使用反向传播算法如随机梯度下降法(SGD)对权值进行不断修正的过程,以输出层的权值为例,其更新公式如下:
其中E为损失函数,μ为学习率。
损失函数原理参考:
机器学习基础知识之损失函数
反向传播原理参考:
神经网络之反向传播算法(梯度、误差反向传播算法BP)
4、建模步骤
以使用径向基神经网络进行预测为例,可以将径向基神经网络预测模型的建模步骤总结如下:
- 根据输入数据的相关特征确定径向基神经网络输入层、隐含层以及输出层的节点数;
- 使用K-means算法对模型的输入数据进行聚类,将聚类生成的中心点作为隐含层径向基函数的中心点,通过中心点计算获得隐含层径向基函数的宽度向量;
- 选择一种参数初始化方法对径向基神经网络输出层的连接权值以及阈值进行随机初始化;
- 数据由输入层输入径向基神经网络,传递至隐含层后经径向基函数对数据进行非线性转换;
- 数据在隐含层输出后传递至输出层,在与输出层的连接权值进行线性计算后由激活函数进行非线性转换,最后得到网络的前向传播输出;
- 选择一种损失函数对网络的前向传播输出以及目标值进行相关计算得到损失值;
- 以输出层的损失值计算得到输出层连接权值以及阈值的梯度,选择一种反向传播算法对它们进行调整;
- 损失值传递至隐含层,同样使用相同的反向传播算法对隐含层的中心点以及宽度向量进行调整;
- 获得一个参数得到更新后的径向基神经网络;
- 在达到最大迭代次数或满足停止迭代条件之前,重复步骤4到步骤9,在达到最大迭代次数后,输出隐含层与输出层参数确定的径向基神经网络。
参数初始化方法参考:
神经网络基础知识之参数初始化
二、径向基神经网络的实现
以数据预测为例,下面介绍基于Python实现径向基神经网络的过程。
选用某省市的表层土壤重金属元素数据集作为实验数据,该数据集总共96组,随机选择其中的24组作为测试数据集,72组作为训练数据集。选取重金属Ti的含量作为待预测的输出特征,选取重金属Co、Cr、Mg、Pb作为模型的输入特征。
1、训练过程(RBFNN.py)
#库的导入
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
#激活函数
def tanh(x):
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
#激活函数偏导数
def de_tanh(x):
return (1-x**2)
#参数设置
samnum = 72 #输入数据数量
hiddenunitnum = 8 #隐含层节点数
indim = 4 #输入层节点数
outdim = 1 #输出层节点数
maxepochs = 500 #最大训练次数
errorfinal = 0.65*10**(-3) #停止迭代训练条件
learnrate = 0.001 #学习率
#输入数据的导入
df = pd.read_csv("train.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
samplein = np.mat([Co,Cr,Mg,Pb])
#数据归一化,将输入数据压缩至0到1之间,便于计算,后续通过反归一化恢复原始值
sampleinminmax = np.array([samplein.min(axis=1).T.tolist()[0],samplein.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值
sampleout = np.mat([Ti])
sampleoutminmax = np.array([sampleout.min(axis=1).T.tolist()[0],sampleout.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值
sampleinnorm = ((np.array(samplein.T)-sampleinminmax.transpose()[0])/(sampleinminmax.transpose()[1]-sampleinminmax.transpose(