刚开始学习机器学习的时候就接触了均方误差（MSE，Mean Squared Error），当时就有疑惑，这个式子是怎么推导的，但是因为懒没有深究。今天看到了唐宇迪老师的机器学习课程，终于理解他是怎么推导的了。一定要一步一步看下去，别看他公式这么多，随便认真看一下就能理解的！

问题描述

我们有工资和年龄两个特征，要预测银行会贷款给我们多少钱？

1. 拟合函数

假设：
年龄：$x_1$
工资：$x_2$
年龄的参数：${\theta }_1$
工资的参数：${\theta }_2$
那么有拟合函数：
（1）

将它转化为矩阵表达形式为：
（2）
其中x0全为1。

2. 误差

真实值和预测值之间通常情况下是会存在误差的，我们用ε来表示误差，对于每个样本都有：
（3）
上标i表示第i个样本。
误差ε是独立并且具有相同的分布，并且服从均值为0，方差为${\theta }^2$的正态分布。
由于误差服从正态分布，那么有：
（4）
将（3）带入（4）中有：
（5）

3. 似然函数

似然函数用于参数估计，即求出什么样的参数跟我们给出的数据组合后能更好的预测真实值，有：
（6）
取（6）式对数，将连乘转化为加法，这也是一般似然函数的求解方法：
（7）
将（7）式展开并化简有：
（8）
（8）式等式右侧的第一项为一个常量，似然函数要取最大值，因而第二项越小越好，有：
（9）
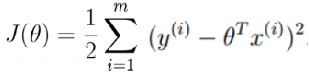
（9）式相当于最小二乘法的式子，即是均方误差的表达式。下一步我们要解出$\theta$的表达式

4. 求导

我们将（9）时表示为矩阵的形式，有：
（10）
接下来需要对矩阵求偏导，矩阵求偏导方法移至矩阵求偏导，过程如下：
（11）
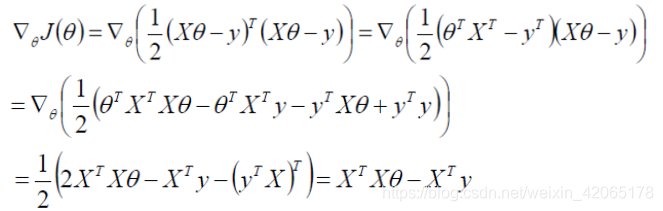
最后解出：
（12）