数据结构—树与二叉树(Part Ⅱ)—二叉树的顺序/链式存储

数据结构-树与二叉树(第七章)的整理笔记，若有错误，欢迎指正。

二叉树的存储结构

顺序存储结构

二叉树的顺序存储结构就是用一组地址连续的存储单元来存放二叉树的数据元素，因此必须确定好树中各数据元素的存放次序，使得各数据元素在这个存放次序中的相互位置能反映出数据元素之间的逻辑关系。
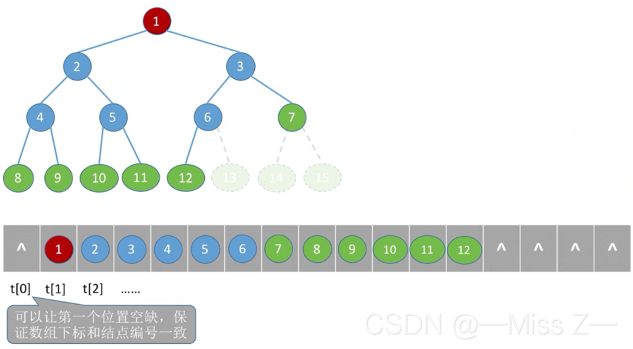
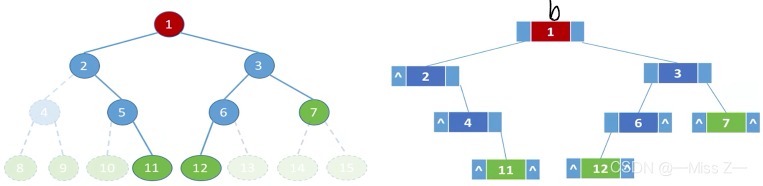
由二叉树的性质4可知，对于完全二叉树和满二叉树，树中结点的层序编号可以唯一的反映出结点之间的逻辑关系，所以可以用一维数组按从上到下、从左到右的顺序存储树中的所有结点值，通过数组元素的下标关系反映完全二叉树或满二叉树中结点之间的逻辑关系。
编号为i的结点值存放在数组下标为i的元素中(’^'表示空结点)。由于C/C++语言中的数组下标从0开始，这里为了一致性而没有使用下标为0的数组元素。
对于一个编号(下标)为i的结点，如果有双亲，其双亲结点的编号(下标)为 $⌊\frac{i}2⌋$ (向下取整)；
如果它有左孩子，其左孩子结点的编号(下标)为 $2 i$ ；
如果它有右孩子，其右孩子结点的编号(下标)为 $2 i + 1$ ；
结点i所在的层次为 $log_2^{n+1}⌉$ 或 $log_2^n⌋+1$ 。

若满二叉树/完全二叉树中共有n个结点，则
• 判断 i 是否有左孩子？—— $2 i \leq n$ ？
• 判断 i 是否有右孩子？—— $2 i + 1 \leq n$ ？
• 判断 i 是否是叶子/分支结点？—— $i≥⌊\frac{i}2⌋$ ？

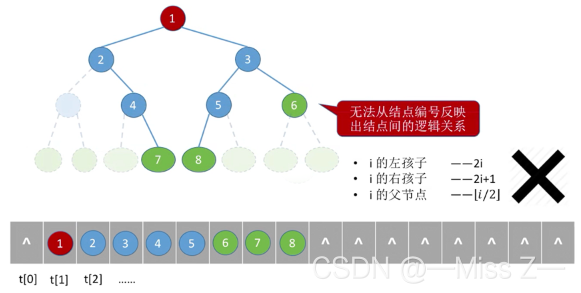
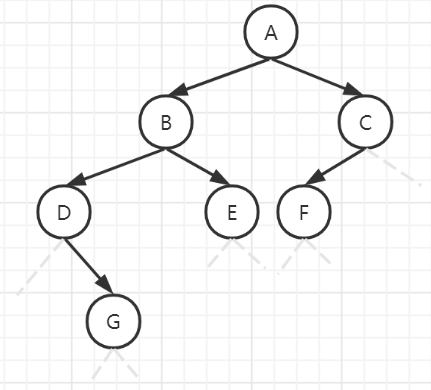
然而对于一般的二叉树，如果仍按照从上到下和从左到右的顺序将树中的结点顺序存储在一维数组中，则数组元素下标之间的关系不能够反映二叉树中结点之间的逻辑关系。
这时可将一般二叉树进行改造，增添一些并不存在的空结点，使之成为一棵完全二叉树的形式。再对所有结点按层序编号，然后仅保留实际存在的结点。接着把各结点值按编号存储到一维数组中，在二叉树中人为增添的结点(空结点)在数组中所对应的元素值为一特殊值，例如’^'字符。
显然，完全二叉树或满二叉树采用顺序存储结构比较合适，既能够最大可能地节省存储空间，又可以利用数组元素的下标确定结点在二叉树中的位置以及结点之间的关系。
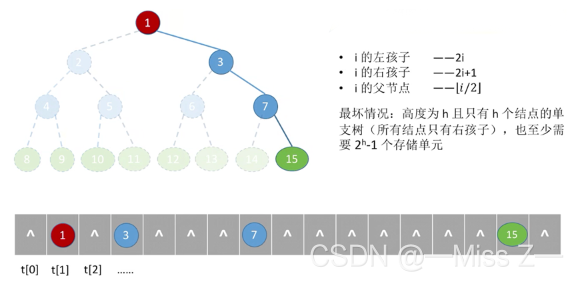
对于一般二叉树，如果它接近于完全二叉树形态，需要增加的空结点个数不多，也可以采用顺序存储结构。如果需要增加很多空结点オ能将一棵二叉树改造成为一棵完全二叉树，采用顺序存储结构会造成空间的大量浪费。最坏情况是右单支树(除叶子结点外每个结点只有一个右孩子)，一棵高度为h的右单支树，只有h个结点，却需要分配 $2^h-1$ 个存储单元在顺序存储结构中，查找一个结点的孩子、双亲结点都很方便。

代码实现

#include<stdio.h>
#include<math.h>
#define h 4 //二叉树的高度
#define MaxSize pow(2,h)-1 //高度为h的满二叉树最多的结点数
typedef char ElemType;
typedef struct
{
	ElemType value; //结点中的数据元素
	bool isEmpty; //结点是否为空
}TreeNode;

void InitTree(TreeNode t[]) //初始化
{
	for (int i = 0; i <= MaxSize; i++)
	{
		t[i].value = 0;
		t[i].isEmpty = true;
	}
}

int CreateTree(TreeNode t[]) //创建二叉树
{
	ElemType data;
	int n = 0, i = 1; //数组下标i从1开始
	printf("输入：");
	scanf("%c", &data);
	while (data != '\n') //换行结束
	{
		t[i].value = data;
		if (data != '#')
		{
			t[i].isEmpty = false;
			n++;
		}
		i++; //数组下标+1
		scanf("%c", &data);
	}
	return n;
}

void DispTree(TreeNode t[], int n) //输出二叉树
{
	printf("value：");
	for (int i = 1; i <= MaxSize; i++)
		printf("\t%c ", t[i].value);
}

bool HaveLeftChil(TreeNode t[], int i) //判断结点i是否有左孩子
{
	if (t[2 * i].isEmpty == true) return false;
	return true;
}

bool HaveRightChil(TreeNode t[], int i) //判断结点i是否有右孩子
{
	if (t[2 * i + 1].isEmpty == true) return false;
	return true;
}

bool Parents(TreeNode t[], int i) //求结点i的双亲结点
{
	if (i == 1) return false; //根节点没有双亲结点
	printf("\n结点i(i=%d)的双亲结点为：%c", i, t[i/2].value);
	return true;
}

bool isBranch(TreeNode t[], int i, int n) //判断结点i是否是分支结点
{
	if (t[i].isEmpty == false && i <= MaxSize / 2)
		return true;
	return false;
}

bool isLeaf(TreeNode t[], int i, int n) //判断结点i是否是叶子结点
{
	if (isBranch(t, i, n) == false) return true; //如果不是分支结点，则为叶子结点
	return false;
}

int Layer(TreeNode t[], int i) //求结点i所在的层次
{
	return log2(i) + 1;
}

int main()  //主函数
{
	TreeNode t[20];
	InitTree(t);
	int n;
	n = CreateTree(t);
	printf("该二叉树共有：%d个结点\n", n);
	printf("-----输出二叉树-----\n");
	printf("i：");
	for (int i = 1; i <= MaxSize; i++)
		printf("\t%d", i);
	printf("\n\t------------------------------------------------------------------------------------------------------------------\n");
	DispTree(t, n);

	int i = 3;
	printf("\n\n-----判断结点i是否有左孩子-----");
	printf("\n结点i(i=%d)有左孩子吗？—— %d", i, HaveLeftChil(t, i));

	printf("\n\n-----判断结点i是否有右孩子-----");
	printf("\n结点i(i=%d)有右孩子吗？—— %d", i, HaveRightChil(t, i));

	int x;
	i = 7;
	printf("\n\n-----求结点i的双亲结点-----");
	printf("\n结点i(i=%d)有双亲结点吗？—— %d", i, Parents(t, i));

	printf("\n\n-----判断结点i是否是分支结点-----");
	printf("\n结点i(i=%d)是分支结点吗？—— %d", i, isBranch(t, i, n));

	printf("\n\n-----判断结点i是否是叶子结点-----");
	printf("\n结点i(i=%d)是叶子结点吗？—— %d", i, isLeaf(t, i, n));

	i = 15;
	printf("\n\n-----求结点i所在的层次-----");
	printf("\n结点i(i=%d)所在的层次为：%d", i, Layer(t, i));
	return 0;
}

运行结果

在这里插入图片描述

链式存储结构

由于二叉树顺序存储结构具有其固有缺陷，使得二叉树的插入、删除等运算十分不方便。因此，对于一般二叉树通常采用链式存储方式。
二叉树的链式存储结构是指用一个链表来存储一棵二叉树，二叉树中的每一个结点用链表中的一个结点来存储。
二叉树链式存储结构中结点的标准存储结构如下：

其中，data表示值域，用于存储对应的数据元素，lchild和 rchild分别表示左指针域和右指针域，分别用于存储左孩子结点和右孩子结点的存储地址。这种链式存储结构通常称为二叉链(binary linked list)。二叉链中通过根结点指针b来唯一标识整个存储结构，称为二叉树b。

在含有n个结点的二叉链表中，共含有2n个指针域，除了根结点之外，其他每一个结点头上都会连一个指针，即有n-1个结点的头上连有指针，因此含有2n-(n-1)=n+1个空链域。
二叉树中结点类型BTNode的声明如下：

typedef struct BTNode
{
	ElemType data; //数据域
	struct BTNode* lchild, * rchild; //左、右孩子指针
}BTNode,*BTNodeTree;

二叉链存储结构的优点是：对于一般的二叉树比较节省存储空间，在二叉链中访问一个结点的孩子很方便，但访问一个结点的双亲结点需要扫描所有结点。

代码实现

#include <stdio.h>
#include<stdlib.h>
typedef char ElemType;
#define MaxSize 20
typedef struct BiTNode
{
    ElemType data;
    struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;

void InitBiTree(BiTNode* t) //初始化二叉树
{
    t = NULL; //构造空二叉树
}

void CreateBiTree(BiTNode*& t) //构建二叉树
{
    ElemType data;
    if ((data = getchar()) == '#') t = NULL;
    else
    {
        t = (BiTNode*)malloc(sizeof(BiTNode));
        t->data = data;
        CreateBiTree(t->lchild);    //创建左子树
        CreateBiTree(t->rchild);    //创建右子树
    }
}

void PreOrder(BiTNode* t) //先序遍历
{
    if (t != NULL) //不是空树时遍历
    {
        printf("%c ", t->data); //访问根节点
        PreOrder(t->lchild); //先序遍历左子树
        PreOrder(t->rchild); //先序遍历右子树
    }
}

void InOrder(BiTNode* t) //中序遍历
{
    if (t != NULL)
    {
        InOrder(t->lchild);
        printf("%c ", t->data);
        InOrder(t->rchild);
    }
}

void PostOrder(BiTNode* t) //后序遍历
{
    if (t != NULL)
    {
        PostOrder(t->lchild);
        PostOrder(t->rchild);
        printf("%c ", t->data);
    }
}

typedef struct
{
    BiTNode* data[MaxSize];
    int front, rear;
}SqQueue;

void InitQueue(SqQueue*& qu)
{
    qu = (SqQueue*)malloc(sizeof(SqQueue));
    qu->rear = qu->front = 0;
}

bool EmptyQueue(SqQueue* qu)
{
    return qu->rear == qu->front;
}

bool enQueue(SqQueue*& qu, BiTNode* b)
{
    if ((qu->rear + 1) % MaxSize == qu->front) return false;
    qu->data[qu->rear] = b;
    qu->rear = (qu->rear + 1) % MaxSize;
}

bool deQueue(SqQueue*& qu, BiTNode*& b)
{
    if (qu->rear == qu->front) return false;
    b = qu->data[qu->front];
    qu->front = (qu->front + 1) % MaxSize;
}

void DestroyQueue(SqQueue*& qu)
{
    free(qu);
}

void LevelOrder(BiTNode* b) //层次遍历
{
    BiTNode* p;
    SqQueue* qu;
    InitQueue(qu);
    enQueue(qu, b);
    while (!EmptyQueue(qu))
    {
        deQueue(qu, p);
        printf("%c ", p->data);
        if (p->lchild != NULL) enQueue(qu, p->lchild);
        if (p->rchild != NULL) enQueue(qu, p->rchild);
    }
    DestroyQueue(qu);
}

int count(BiTNode* t) //求结点总数
{
    int sum = 0;
    if (t == NULL) sum = 0; //空树的情况 
    else sum = 1 + count(t->lchild) + count(t->rchild);
    return sum;
}

int count_leaf(BiTNode* t) //求叶子结点个数并输出
{
    int sum = 0;
    if (t == NULL)  sum = 0; //空树的情况
    else if (t->lchild == NULL && t->rchild == NULL)
    {
        sum = 1; //只有根节点的情况
        printf("%c ", t->data);
    }
    else sum = count_leaf(t->lchild) + count_leaf(t->rchild);
    return sum;
}

int Depth(BiTNode* t) //求深度
{
    if (t == NULL) return 0;
    int left = Depth(t->lchild); //左子树的深度
    int right = Depth(t->rchild); //右子树的深度
    return left > right ? left + 1 : right + 1; //树的深度=Max(左子树深度，右子树深度)+根节点
}

void DestoryBiTree(BiTNode*& t) //销毁二叉树
{
    if (t != NULL)
    {
        if (t->lchild) DestoryBiTree(t->lchild);
        if (t->rchild) DestoryBiTree(t->rchild);
        free(t);
        t = NULL;
    }
}

BiTNode* FindNode(BiTNode* t, ElemType x)
{
    BiTNode* p;
    if (t == NULL) return NULL;
    else if (t->data == x) return t;
    else
    {
        p = FindNode(t->lchild, x);
        if (p != NULL) return p;
        else return FindNode(t->rchild, x);
    }
}

BiTNode* LchildNode(BiTNode* p) //返回结点p的左孩子指针
{
    return p->lchild;
}

BiTNode* RchildNode(BiTNode* p) //返回结点p的右孩子指针
{
    return p->rchild;
}

int Level(BiTNode* t, ElemType x, int h) //查找结点x所在的层次
{
    int lev;
    if (t == NULL) return 0;
    else if (t->data == x) return h;
    else
    {
        lev = Level(t->lchild, x, h + 1); //在左子树中查找
        if (lev != 0) return lev; //在左子树中找到了，返回lev
        else return Level(t->rchild, x, h + 1); //在左子树中未找到，再到右子树中查找
    }
}

int main()
{
    BiTNode* t, * p, * lchild, * rchild;
    printf("请输入元素，#表示空树：\n");
    CreateBiTree(t);
    printf("\n先序遍历：");
    PreOrder(t);
    printf("\n中序遍历：");
    InOrder(t);
    printf("\n后序遍历：");
    PostOrder(t);
    printf("\n");
    printf("层次遍历：");
    LevelOrder(t);
    printf("\n");

    printf("\n-----输出二叉树的深度以及总结点数-----\n");
    printf("深度：%d\n", Depth(t));
    printf("总结点数：%d\n", count(t));

    printf("\n-----输出二叉树中的叶子结点-----\n");
    printf("\n叶子结点有：%d个\n", count_leaf(t));

    ElemType x;
    x = 'B';
    p = FindNode(t, x);
    printf("\n-----求结点%c的孩子结点-----\n", p->data);
    lchild = LchildNode(p);
    printf("结点%c的左孩子为：%c\n", p->data, lchild->data);
    rchild = RchildNode(p);
    printf("结点%c的右孩子为：%c\n", p->data, rchild->data);

    int h;
    printf("\n-----返回结点x所在的层次-----\n");
    printf("结点%c所在的层次为：%d", x, Level(t, x, 1));

    DestoryBiTree(t);
    return 0;
}

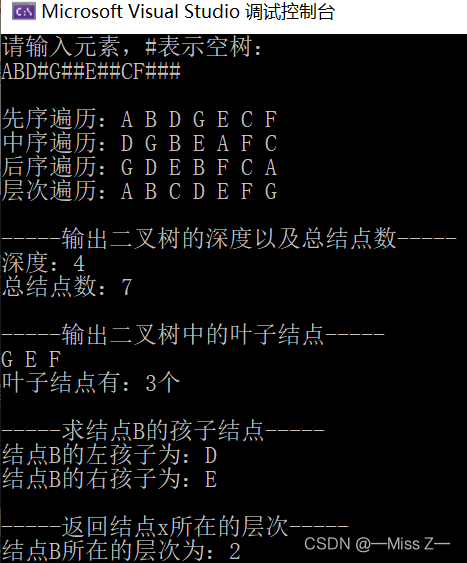
运行结果

在这里插入图片描述

有时为了高效地访问每个结点的双亲结点，可在每个结点中再增加一个指向双亲的指针域parent，这样就构成了叉树的3叉链表，其结点结构如下：

typedef struct BTNode
{
	ElemType data; //数据域
	    struct BiTNode* lchild, * rchild, * parent; //左、右孩子以及父节点指针
}BTNode,*BTNodeTree;

数据结构—树与二叉树(Part Ⅱ)—二叉树的顺序/链式存储

二叉树的存储结构

顺序存储结构

代码实现

运行结果

链式存储结构

代码实现

运行结果

悦读