设计功能：

1.  正弦信号绘制

考虑到绘制的界面大小有限，所有信号统一绘制四个周期，如果是两个正弦相加或相乘，将会绘制频率小的四个周期，每个周期都会在x轴显示时间，单位秒，来表示不同频率的信号。即x(t)=Asin(2πfat)。检查时发现幅度显示有误，有机会会改。

2.  对两个正弦信号相加和相乘

可以选择是加法型还是乘法型，红字代表当前的状态，fa1，A1是一信号的频率和幅度，fa2和A2是二信号的频率和幅度。默认状态时，二信号的A2都是零。fa会自动取fa1和fa2中较小且不为零的值，来保证绘制的连续信号是频率小的四个周期。后续有机会可以加上相位φ；还可以加更多信号的功能，甚至可以单独为信号合成设计界面。当有一个信号幅度较小，频率较小，另一个信号幅度较大，频率较大，可以观测出明显的包络线现象。

3.  对连续信号采样成离散信号。

fs是采样频率。N是截取长度。对连续信号进行采样。x(n)=Asin(2πnfa/fs)。fs过小时，加法时，小于fa1和fa2中大的那个两倍时；乘法时，小于fa1和fa2乘积，且fa1，fa2都不为零时，会产生混叠现象；当N不是fs/fa的整数倍时会产生泄露现象，多个信号合成时，N不是任一fs/fan的整数倍时，都会产生泄露现象。由于界面有限，N过大时，大于一两千图就不清楚了，后续有机会可以单独为信号离散化设计界面。

4.  对离散信号DFT，绘制频谱图，记录算法效率

根据DFT公式，将其中的W写成e的指数形式，再展开成三角函数形式，将实部虚部分开存储，从而避免虚数j。X[n].Re=∑x(n)*cos(2πnm/N),0<=n<=N-1;X[n].Im=-∑x(n)*sin(2πnm/N),0<=n<=N-1。幅频图|X(n)|=(X[n].Re^2+X[n].Im^2)½,相频图φ[n]=atan(X[n].Im/X[n].Re)。

5.  对离散信号FFT，绘制频谱图，记录算法效率

根据FFT公式，同理。G[n].Re=∑x(2n)*cos(4πnm/N),0<=n<=N/2-1;G[n].Im=∑x(2n)*sin(4πnm/N),0<=n<=N/2-1;H[n].Re=∑x(2n+1)*cos(2π(2n+1)m/N),0<=n<=N/2-1;H[n].Im=∑x(2n+1)*sin(2π(2n+1)m/N),0<=n<=N/2-1;之后X[n].Re=G[n].Re+H[n].Re; X[n].Im=G[n].Im+H[n].Im; X[n+N/2].Re=G[n].Re-H[n].Re; X[n+N/2].Im=G[n].Im-H[n].Im。由于当N很小时，计算机计算时间很短，1ms不到，没有手段检测。一开始采取在最里层循环加延时1ms，这样大部分情况FFT都比DFT快，但强制延时会有不可抗的冲突，效率比一直会变，甚至有时DFT比FFT都快；所以又将这个延时改成了一个+1的计数，这样这个效率比是关于N的固定函数值。DFT和FFT在幅频图一致，但相频图有不一致的点，这些点的幅度都为零，我们暂时认为没有影响。

6.  对DFT后的结果IDFT，绘制还原后的离散信号

根据IDFT公式，用X[n]反求x[n]。x[n].Re=1/N*∑(X(n).Re*cos(2πnm/N)- X(n).Im*sin(2πnm/N)),0<=n<=N1;x[n].Im=1/N*∑(X(n).Im*sin(2πnm/N)+X(n).Re*sin(2πnm/N)),0<=n<=N-1；最后x[n]= (x[n].Re^2+x[n].Im^2)½。还原后的离散信号全为正值。后续有机会可以用内插函数还原成连续信号x(t)。

算法过程：

1.  采样算法：

2.  DFT算法：

3.  FFT算法：

4.  IDFT算法：

演示结果：

1.  不同单一频率正弦信号绘制：

上图为fa1=1HZ时。

上图为fa1=100HZ时。

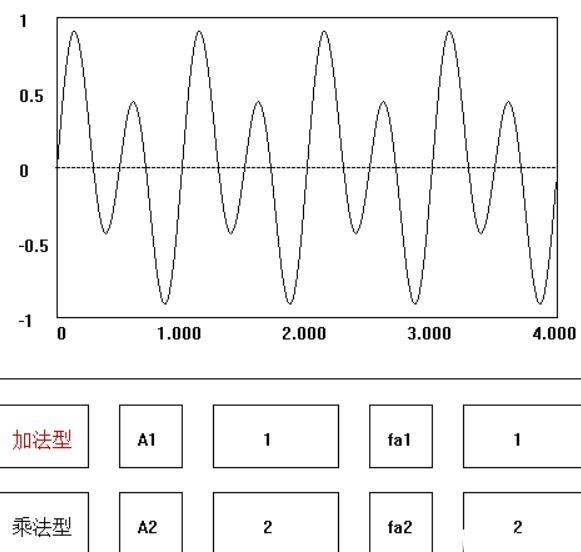
2.  正弦信号相加以及产生包络线：

上图是两个简单正弦波相加

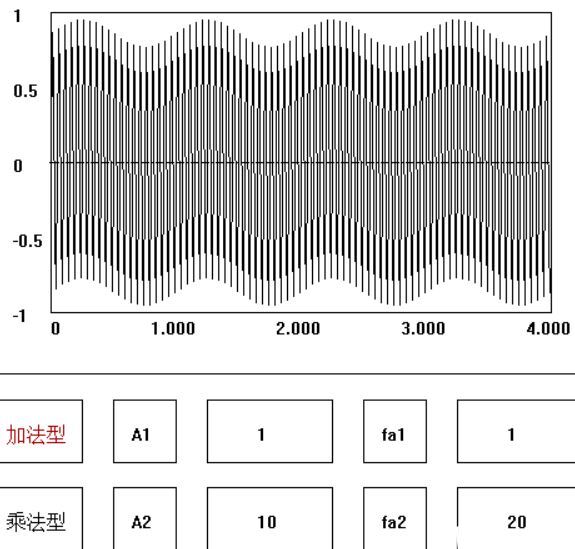
上图是两个正弦波相加产生包络线(幅度相加，不同于高频学的频率相加，所以包络线不一样)

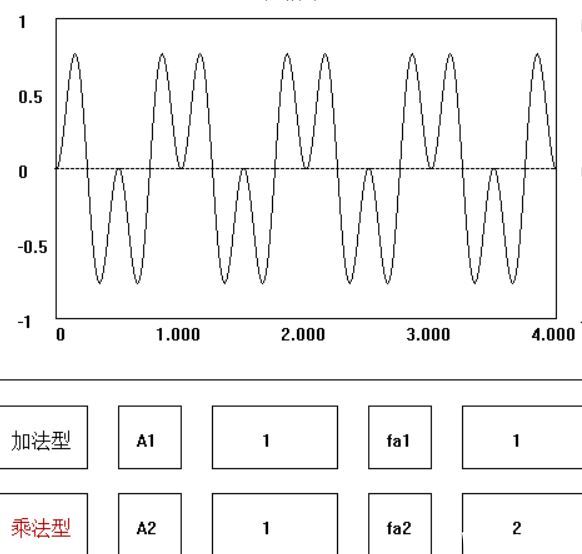
3.  正弦信号相乘：

上图是两个简单正弦波相乘

上图是两个正弦波相乘(幅度相乘)

4.  同一