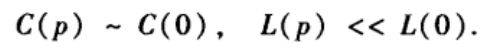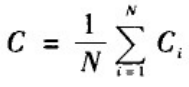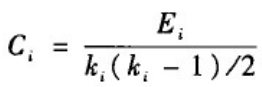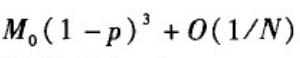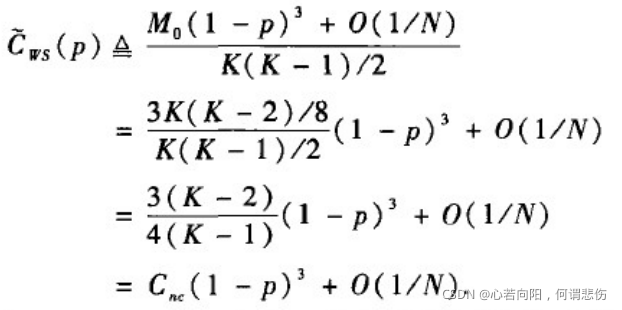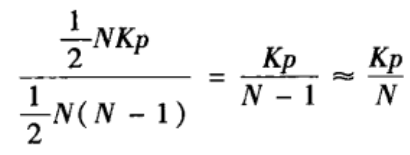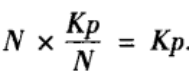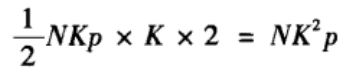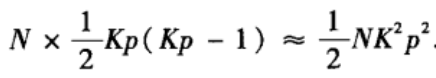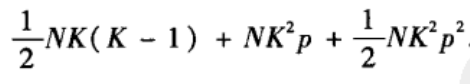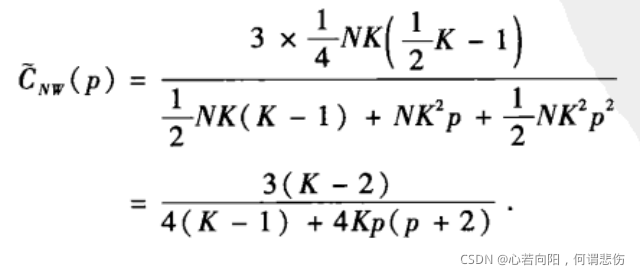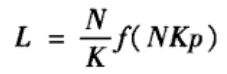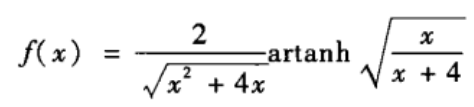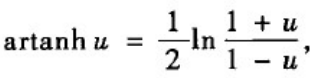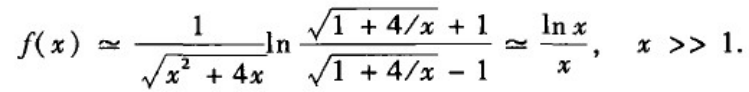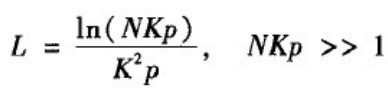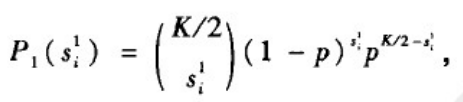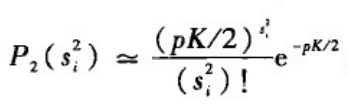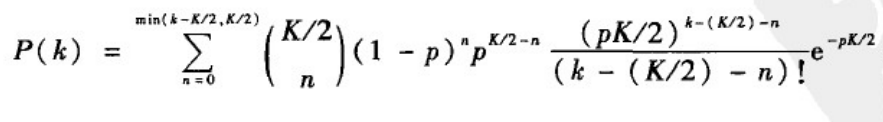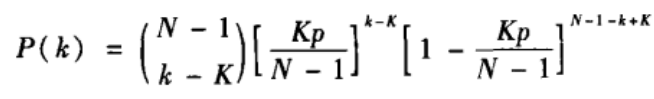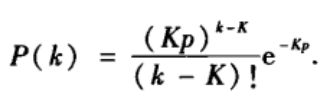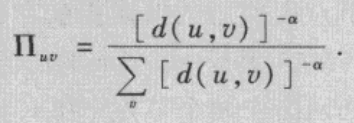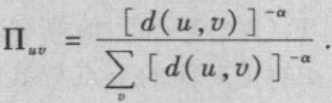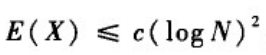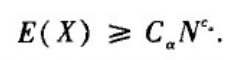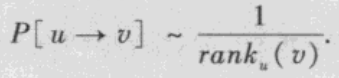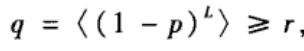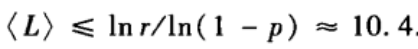一、小世界网络模型

1、WS小世界模型

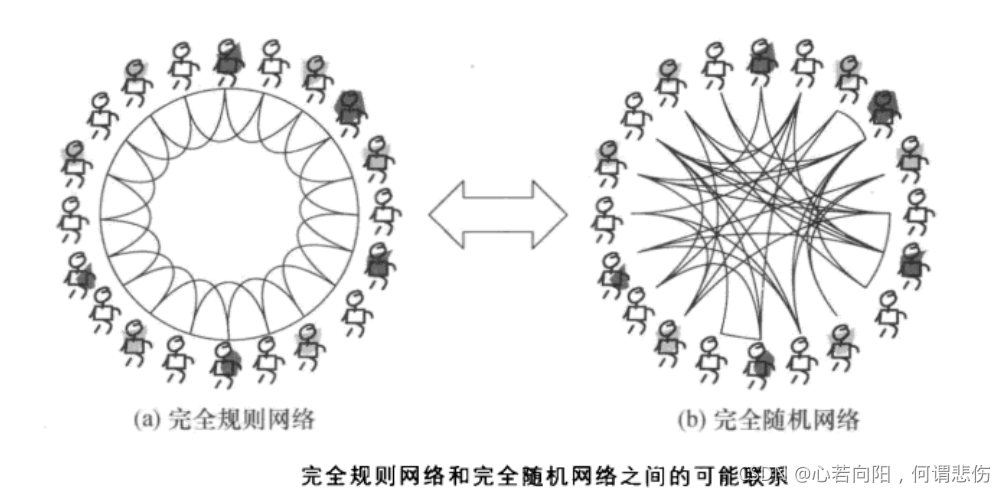
我们在前面的文章中介绍过，上图（a）所示的完全规则的最近邻耦合网络具有较高的聚类特性，但并不具有较短的平均距离。另一方面，完全随机的ER随机图虽然具有小的平均路径长度却没有高聚类特性。因此，规则的最近邻网络和ER随机图都不能再现许多实际网络同时具有的明显聚类和小世界特征。从直观上看，毕竟大部分实际网络并不是完全规则或完全随机的。
WS小世界模型构造算法：
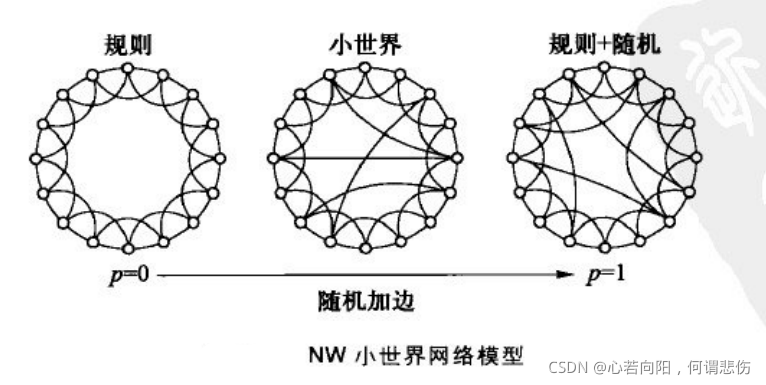
（1）从规则图开始：给定一个含有N个点的环状最近邻耦合网络，其中每个节点都与它左右相邻的各K/2个节点相连，K是偶数。
（2）随机化重连：以概率p随机地重新连接网络中原有地每条边，即把每条边的一个端点保持不变，另一个端点改取为网络中随机选择的一个节点。其中规定不得有重边或者自环。
在上述模型中，p=0对应于完全规则网络，p=1对应于完全随机网络，通过调节参数p的值就可以实现从规则网络到随机网络的过渡。

2、仿真分析

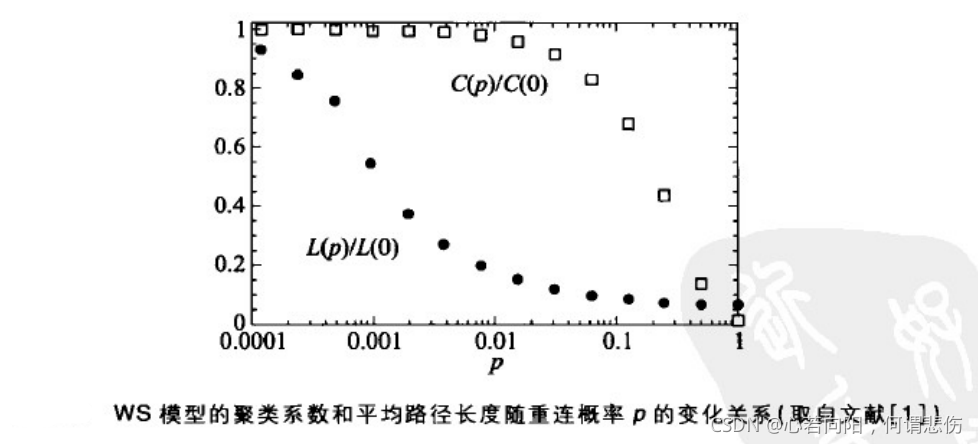
由上述构造模型算法得到的WS模型的聚类系数C§和平均路径长度L§都可看作是重连概率p的函数。

上图显示了在给定参数N=1000，K=10下，网络的聚类系数和平均路径长度随重连概率p的变化关系。
上图的一些科学处理方法值得我们学习：
（1）归一化处理：图中并没有直接画出C§和L§，而是对这两个量做了归一化处理，即为C§/C(0)，L§/L(0)，从而使得两个量的最大值均为1。一般而言，要把不同的量的变化趋势绘制在同一张图中，应该尽可能使得这些量具有统一的尺度。
（2）对数化坐标，图中横坐标取得是对数坐标。这是因为这里重点关注的是p较小时的聚类系数和平均路径长度的变化情形，采用对数坐标的好处就在于可以在横轴上把较小p值的刻度拉宽而压缩较大p值的区间。
（3）平均化处理：考虑到随机性，图中的数据是20次平均的结果。一般而言，在做含有随机性的实验时，应尽可能考虑做多次实验然后取平均，从而保证所得到的结果的合理性。
上图中当p从零开始增大时，随机重连后的网络的聚类系数下降缓慢但平均路径长度却下降很快。即当p较小时

这意味着，当重连概率p较小时，网络即具有较短的平均路径长度又具有较高的聚类系数。

3、实验验证

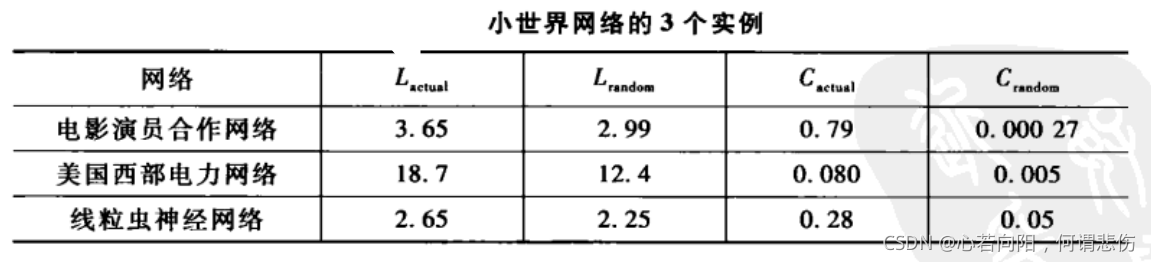
前人们在仿真分析后计算了3个实际网络的平均路径长度L${}_{actual}$和聚类系数，C${}_{actual}$，并与相应的具有相同节点数和平均度的随机图的平均路径长度L${}_{random}$和平均聚类系数，C${}_{random}$相比较。这三个网络分别是：
电影演员合作网络：N=225226，< k>=61；
美国西部电力网络：N=4941，< k>=2.67；
线粒虫神经网络：N=225226282，< k>=14；
这三和实际网络具有如下共同特征：L${}_{actual}$稍大于L${}_{random}$，C${}_{actual}$远大于C${}_{random}$。

4、动力学分析

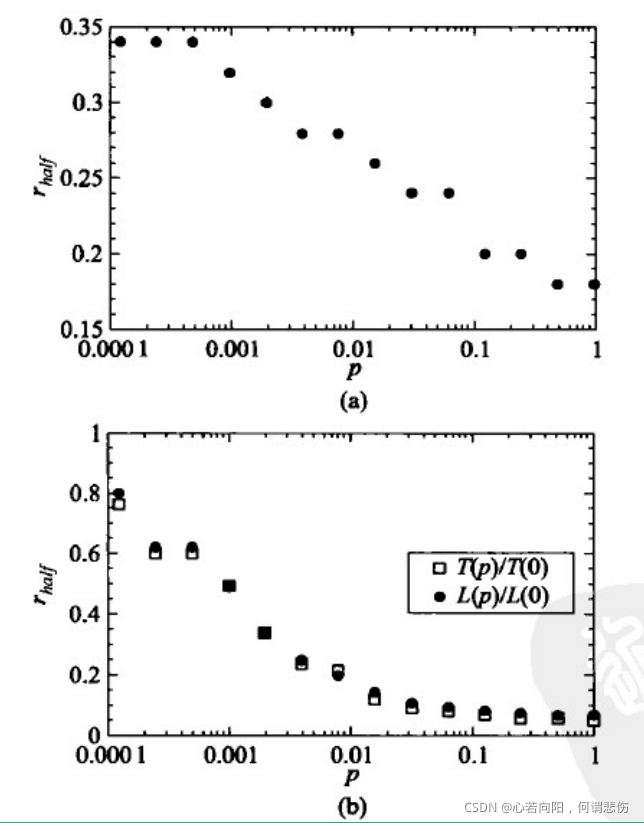
前人通过仿真研究了WS小世界模型上的病毒传播动力学。初始时刻网络中仅有单个个体感染病毒，然后在各时刻每个感染个体以概率r感染健康的邻居节点。上图(a)显示的是病毒感染一半人口的临界传染概率r${}_{half}$r与WS模型的重连概率p的关系。可以看出，当重连概率p从零增大时，r${}_{half}$快速下降。如果固定r=1，那么只要网络是连通的，病毒就总能感染网络中的所有节点。从图(b)可以看出，病毒扩散至整个网络(即所有节点都被感染)所需时间T§与平均距离长度L§随着WS模型重连概率p的变化趋势几乎一致，从而表明病毒在小世界网络中传播更快。
在WS模型提出之后，人们自然希望进一步对该模型的性质做理论分析。不久之后,Newman和Watts提出了另一个在理论分析方面相对容易处理的小世界模型，现在称为NW小世界模型。

5、NW小世界模型

NW模型是通过用“随机化加边”取代WS模型构造中的“随机化重连”而得到的。注意到在WS模型中，边的数目固定为NK/2，但是以概率p对这些边进行随机重连，这意味着随机重连得到的长程边数目的均值为NKp/2。在NW模型中，原来的NK/2条边保持不变，而是在此基础上再随机添加一.些边，为便于比较，这些添加的长程边数目的均值同样取为NKp/2。NW模型的具体构造算法如下：
（1）从规则图开始：给定一个含有N个节点的环状最近邻耦合网络，其中每个节点都与它左右相邻的各K/2个节点相连，K是偶数。
（2）随机化加边：以概率p在随机选取的NK/2对节点之间添加边，其中规定不得有重边和自环。
在p=0时，WS模型和NW模型都对应于原来的最近邻耦合网络；在p=1时，WS模型相当于随机图，而NW模型则相当于在规则最近邻耦合网络的基础上再叠加一个一定边数的随机图。当p足够小而N足够大时，可以认为WS模型和NW模型是等价的。

二、拓扑性质分析

1、聚类系数

1.1 WS小世界网络

网络的聚类系数C定义为网络中所有节点的聚类系数的平均值：

其中。网络中一个度为k${}_i$的节点i的聚类系数C${}_i$定义为：

这里E${}_i$和k${}_i$(k${}_i$-1)/2分别为节点i的k${}_i$个邻居节点之间实际存在的边数和可能存在的最大边数。考虑到WS模型的随机性，我们通过上式的分子和分母的均值来估计聚类系数的均值。分母k${}_i$(k${}_i$-1)/2的均值显然是K(K-1)/2。下面计算
E${}_i$的均值为：

其中M${}_0$为K个邻居节点之间的边数。
所有WS模型的聚类系数的估计值如下：

可以看出聚类系数估计值函数是重连概率p的单调递减函数，这意味着随着随机性的增强，网络的聚类效应减弱。

1.2 NW小世界网络

在前面的文章中我们介绍过可以用网络中三角形的相对数量来刻画网络的聚类特性：

现在基于这一定义来计算NW小世界网络模型的聚类系数。
（1）计算网络中三角形的数目
p=0时，最近邻耦合网络中的三角形数量为$\frac{1}{4}$NK($\frac{1}{2}$K-1)。p>0时，这些三角形在NW模型中仍然保留，现在我们需要计算在添加了长程边之后新增加的三角形的数量。网络中长程边的的平均数为$\frac{1}{2}$NKp，这些边可以在$\frac{1}{2}$N(N-1)个点对之间添加，从而每一对节点之间有长程边的相连的概率为

包含一条长程边的三角形数量近似为一个与N无关的常数：

当网络规模N趋于无穷时，这一常数与最近邻耦合网络的三角形数量O(N)相比是可以忽略不记的。同样，包含两条或三条长程边的三角形数量也可以忽略不记。因此，对于0<=p<<1，NW模型中的三角形数量近似为$\frac{1}{4}$NK($\frac{1}{2}$K-1)。
（2）计算网络中连通三元组的数量
最近邻耦合网络中连通三元组数量为$\frac{1}{2}$NK(K-1)。每条长程边都可以与N条边的两个端点之一形成连通三元组。因此包含一条长城边的连通三元组的平均数量为：

如果一个节点与m>1条长程边相连，那么从中任选两条长程边就构成一个连通三元组，共有$\frac{1}{2}$m(m-1)中可能。平均一个节点与Kp条长程边相连，因此网络中以一个节点为中心的包含两条长程边的连通三元组数量的均值为：

综上所述，NW模型中总的连通三元组的数量的均值为：

所以，当0<=p<<1时，NW小世界网络模型的聚类系数的估计值为：

2、平均路径长度

关于NW或WS小世界模型的平均路径的理论分析至今仍然是很困难的事情，人们还没有得到这两个模型的平均路径长度L的精确解析表达式。已有研究表明，小世界模型的平均路径长度应该具有如下形式：

其中f(u)为一与模型参数无关的普适标度函数。目前还没有f(u)的精确显式表达式，只是给出了如下的近似表达式：

我们可以基于上述两个式子推得平均路径长度是网络规模的对数增长函数。基于关系式

f(u)可以写为：

把上式代入到平均路径长度中，可得

NKp是网络中随机添加的长城边数目均值的两倍，上式意味着：只要网络中随机添加的边的绝对数量足够大(但是占整个网络边数的比例任然可以相当小)，平均路径长度就可以视为网络规模的对数增长函数。

3、度分布

3.1 WS小世界网络

WS模型在重连概率p=0时，每个节点的度都为K(偶数) ，亦即每个节点都与K条边相连：在p>0时，基于WS模型的随机重连规则的实现算法，每个节点仍然至少与顺时针方向的K/2条原有的边相连，亦即每个节点的度至少为K/2。为此，不妨记节点i的度为k${}_i$=s${}_i$+ K/2，s${}_i$为整数。
进一步地，s${}_i$可分为两部分s${}_i$=s${}_i^1$+s${}_i^2$，s${}_i^1$表示在原有的与节点i相连的逆时针方向的K/2条边中仍然保持不变的边的数目，其中每条边保持不变的概率为1-p，s${}_i^2$表示通过随机重连机制连接到节点i上的长程边，每条这样的边的概率为p/N。我们有

当N充分大时：

对于任一度为k>=K/2的节点s${}_i^1\in$[0，min(k-K/2,K/2)]。因此，当k>=K/2时

而当k<K/2时，p(k)=0。

3.2 NW小世界网络

在基于“随机加边”机制的NW模型中，由于原有的规则最近邻网络中的所有边保持不变，每个节点的度至少为K。当k<K时，P(k)=0。当k≥K时，一个节点的度为k就意味着有k-K条长程边与该节点相连。之前我们说过每一对节点之间有边相连的概率为Kp/(N-1)。因此，一个随机选取的节点的度为k的概率为

NW模型中长程边的平均数为$\frac{1}{2}$NKp。因此，平均而言，网络中与每个节点相连的长程边的数量为Kp，当N充分大时，二项分布可写为如下泊松分布：

上式为近似等式，当N无穷大时成立。

三、Kleinberg模型与可搜索性

1、Kleinberg模型

二维Kleinberg模型构造算法：
（1）从规则网格开始：给定一个含有N=$\bar{N}\times \bar{N}$个点的最近邻耦合网络，他们分布在一个二维网络上，使得每一行和每一列都恰好有$\bar{N}$个节点。每个节点都通过有向边指向所有与该节点的网格距离不超过p>=1的节点。
（2）随机化加边：对于每个节点，添加从该节点指向网络中的其它q个节点的q条有向边，其中节点u有添加边指向节点v的概率为：


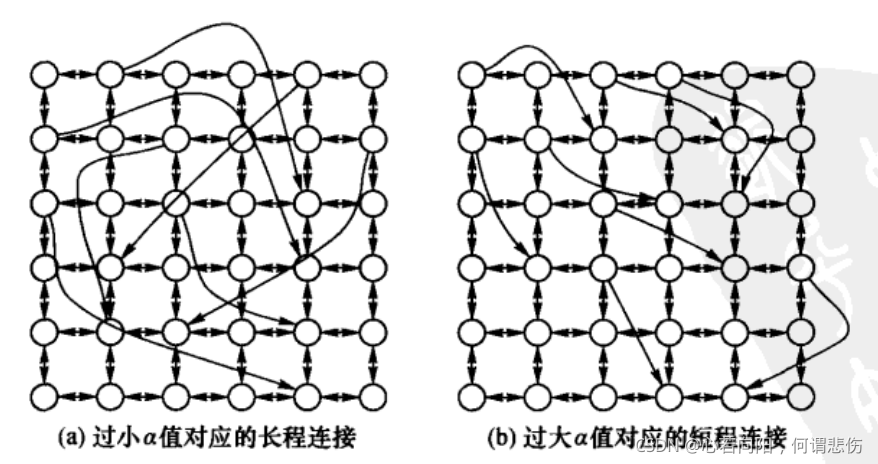
随着参数$\alpha$值的增加，两个在网络距离上相隔较远的节点之间有长程连接的概率越来越小。当$\alpha$很大时，添加的边几乎都成为了短程连接。
上述表明，以规则网络为基础添加连边时，过分的随机和过分的规则都不利于网络上的搜索。所以，是否存在规则性和随机性之间的最佳折中，即最理想的$\alpha$值，使得生成的网络即是小世界又便于快速分散式搜索。

2、最优网络结构

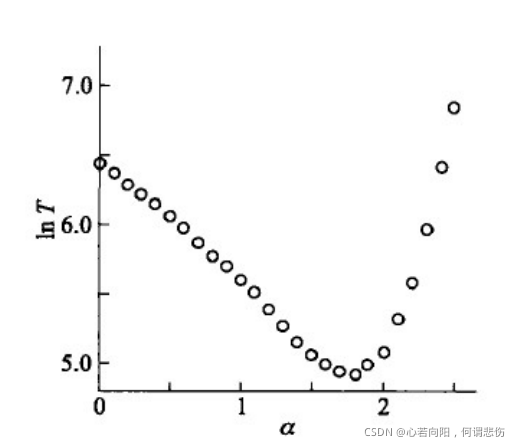
上图为平均传递步数的对数与$\alpha$值的关系。可以发现当N趋于无穷时$\alpha$=2是唯一的最优值。
Kleinberg定理：考虑二维Kleinberg网络模型上的搜索问题，假设每个节点采用的都是局部信息的分散式算法，我们有：
（1）对于0<=$\alpha$<2，存在一个与p，q，$\alpha$相关但与N无关的常数c${}_{\alpha }$，使得对于任意的分散式算法，平均传递步数都有一个下界c${}_{\alpha }$N${}^{(2-\alpha )/3}$。
（2）当$\alpha$=2时，当前信的持有节点只需把信件传递给一个在网格距离上最接近目标节点的邻居节点，这种分散式算法的平均传递步数有一个上界c${}_2$ (logN)${}^2$，其中c${}_2$是一个与N无关的常数。
（3）对于$\alpha$>2，存在一个与p、q、$\alpha$相关但与N无关的常数c${}_{\alpha }$，使得对于任意的分散式算法，平均传递步教都有一个下界c${}_{\alpha }$N${}^{(\alpha -2)/(\alpha -1)}$。

3、Kleinberg模型的理论分析

一维Kleinberg模型有向小世界模型构造算法：
（1）从规则网络开始：给定一个含有N个点的环状最近邻耦合网络，其中每个节点都有边指向与它左右相邻的各K/2个节点，K是偶数。
（2）随机化加边：对于每个节点，添加从该节点指向网络中的其它q个节点的q条有向边，其中节点u有添加边指向节点v的概率与这两个节点之间的格子距离成正比，即有

对于网络中随机选取的源节点s和目标节点t，我们要估计基于局部信息的贪婪算法所需的搜索步数X的期望值E(X)。
（1）当$\alpha$=1时，期望搜索步数上界与网络规模的对数的平方成正比，即存在常数c，使得

（2）当$\alpha \ne$ 1时，期望搜索的步数的下界与网络规模的幂函数成正比，即存在与$\alpha$有关的常数C${}_{\alpha }$和c${}_{\alpha }$>0，使得

4、在线网络实验认证

基于Kleinberg模型得到的结论在多大程度上符合实际呢？
在Kleinberg模型中有两个基本假设:
（1）两个节点之间存在长程连接的概率是由它们之间的网格距离(对应于现实世界的地理距离)决定的。这种只依赖于地理距离建立的长程连接与实际情形的兰只有多大?或者说，在网络搜索中地理因素起着多大的作用?
（2）所有节点在空间上是均匀分布的。但是在现实世界中，节点的分布往往是高度非均匀的：有些区域节点集中，有些区域则节点稀疏。这种非均匀的节点分布对搜索又会带来什么样的影响?
通过前人的实验表明：
（1）从可搜索性的角度看，在Kleinberg理论模型中仅考虑地理因素对长程连接的影响是合理的；也就是说，在这样的理论模型下是可以找到较短路径的。
（2）从最优性的角度来看，基于秩的模型可能更加符合实际。
基于秩的二维经纬网络模型构建：
（1）构建规则经纬网络：N个点分布在一个二维网格上，每个节点都与其4个方向的最近的4个邻居节点之间有短程连接。
（2）基于秩的随机化加边：每个节点u添加一条长程连接，它指向节点v的概率为：

四、层次树结构网络模型与可搜索性

Watts等人提出了另一个基于层次树的社会结构的模型，从另一角度解释了社会网络的可搜索性。

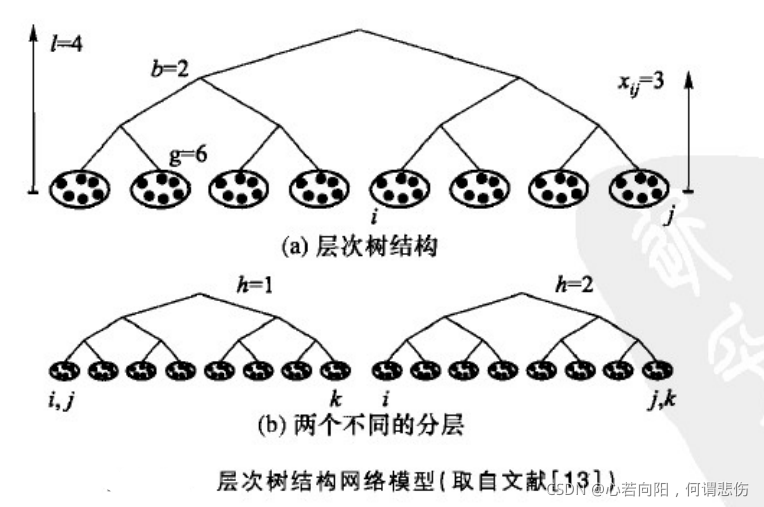
在一个层次树状结构中，定义节点i和j最低的共同上级所在的层数为它们之间的距离x${}_{ij}$；当节点i和j在同一个群中时，x${}_{ij}$=1。节点i和j向上找到的共同祖先的层数越高，它们之间的距离就越大，如上图所示，其中l为层数，b为分叉率，g为群体大小。个体(用点表示)首先聚集成群(用椭圆表示)，然后小的群再聚集成更大的群，这样一直继续下去就形成了一个层次树结构。
假设人们是基于局部信息和贪婪算法向邻居传递消息。当前节点i所知道的信息为自己的坐标向量v${}_i$，节点i在网络中所有邻居j的坐标向量以及目标节点t的坐标向量v${}_t$，而不知道所有其他节点的信息。那么在什么条件下网络可以实现快速搜索呢?也就是说，在什么条件下可以找到随机选择的源节点s和目标节点t之间的较短的传递步数？Watts等考虑了消息前传有一个损耗率p≈0.25，即每一步消息终止的概率为0.25。网络实现快速搜索的判据是，消息最终到达目标节点的概率q不低于设定值r=0.05,即

最大平均传递步数< L >可以近似的由一个与网络规模N无关的常数估计：