高效的分治排序
快速排序是冒泡排序的改进版,是目前已知的最快的排序方法。
该排序算法的基本思想是:
1.先从数列中取出一个数作为基准数。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。
优点:极快,数据移动少;
缺点:不稳定。
算法实现
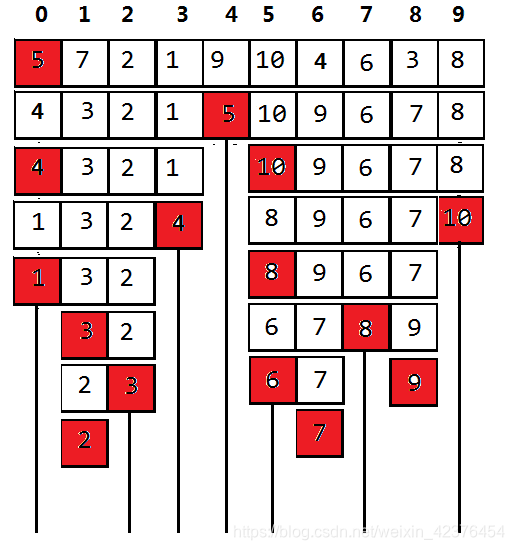
假设我们现在要对{5,7,2,1,9,10,4,6,3,8}这个数组进行快速排序,我们应该怎么怎么做呢?
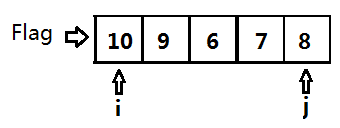
1.立Flag
Flag就是我们之前提到的基准数,为了将数据分区,立Flag是第一步也是最关键的一步。在这里我们将数组的第一个数设为基准数。
2.探测
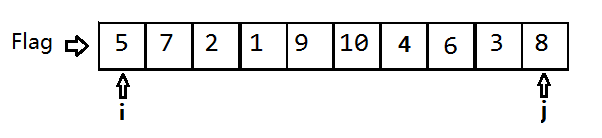
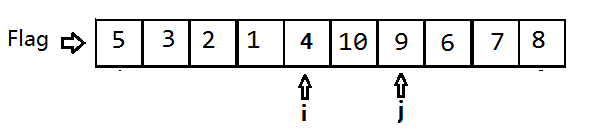
对于{5,7,6,1,9,10,4,2,3,8}这个数组,第一次排序我们的Flag是5,我们分别从数组的左右两端开始“探测”。
我们定义i指向数组的最左端,定义j指向数组的最右端。首先将j向左移,直到j指向的数小于5;再将i向右移,直到i指向的数大于5。最终i指向7,j指向3。
3.交换
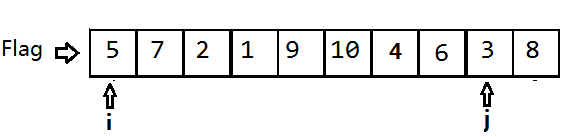
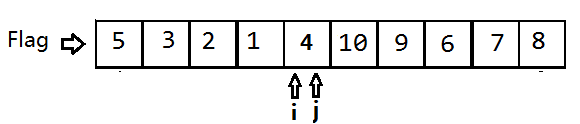
将3和7交换,数组变为{5,3,2,1,9,10,4,6,7,8}。第一次交换结束。
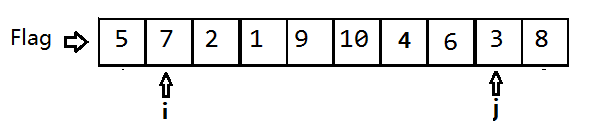
接下来继续探测、交换,探测、交换…
4.Flag落位
第二次交换结束后数组变为{5,3,2,1,4,10,9,6,7,8}。
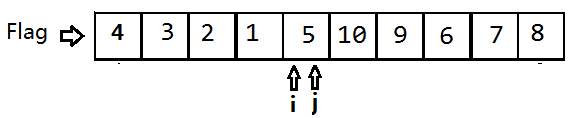
j指向9的位置,i指向4的位置,j继续向左移动,直到i的位置才找到小于5的值。
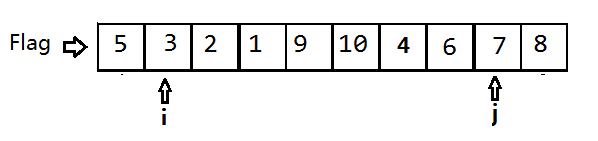
此时i=j,我们只需将Flag落在这个位置:将5和4的值交换。数组变为{4,3,2,1,5,10,9,6,7,8}。
至此,5这个Flag完成了它的历史使命,第一轮交换结束。
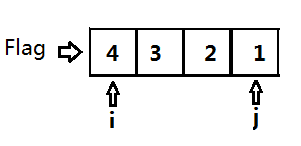
数组被划分为两个区,Flag左边是小于Flag的{4,3,2,1},Flag右边是大于Flag的{10,9,6,7,8}。
5.递归
我们再分别对这两个区进行第二轮交换,交换结果是{1,3,2,4}和{8,9,6,7,10}
对于{1,3,2}和{8,9,6,7}重复进行以上操作,直至得到不能拆解的单个数字,排序完成!
下面用图展示整个排序过程:
6.JAVA代码
public class QuickSort {
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high){
return;
} i=low;
j=high;
//temp就是基准位
temp = arr[low];
while (i<j){
//先看右边,依次往左递减
while (temp<=arr[j]&&i<j){
j--;
}
//再看左边,依次往右递增
while (temp>=arr[i]&&i<j){
i++;
}
//如果满足条件则交换
if (i<j){
t=arr[j];
arr[j]=arr[i];
arr[i]=t;
}
}
//最后将基准为与i和j相等位置的数字交换
arr[low] = arr[i];
arr[i] = temp;
//递归调用左半数组
quickSort(arr, low, j-1);
//递归调用右半数组
quickSort(arr, j+1, high);
}
public static void main(String[] args){
int[] arr = {6,1,2,7,9,11,4,5,10,8};
quickSort(arr, 0, arr.length-1);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}}