1.AES的工作原理
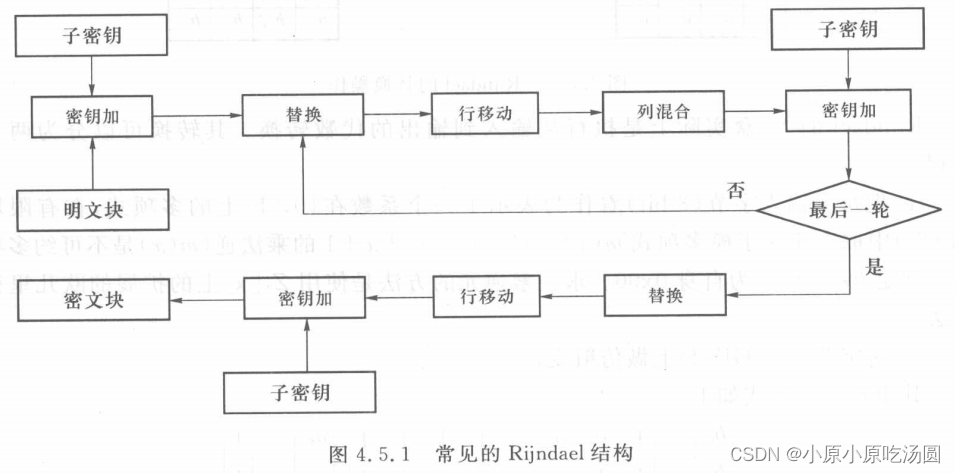
Rijndael是一种灵活的算法,其块的大小可变(128bit、192bit或256bit),密钥大小可变(128bit、192bit或256bit),迭代次数与块和密钥大小有关,因此迭代次数也可变(10,12或14)。常见的Rijndael结构如下图所示。Rijndael不像DES那样在每个阶段中使用替换和置换,而是进行多重循环的替换(Substitution)、行移位(ShiftRow)、列混合(Mixcolumn)和密钥加(Key Add)操作。本文把术语AES和Rijndael视为等价,可交替使用,同时,如无特别说明假设块的大小为128位。
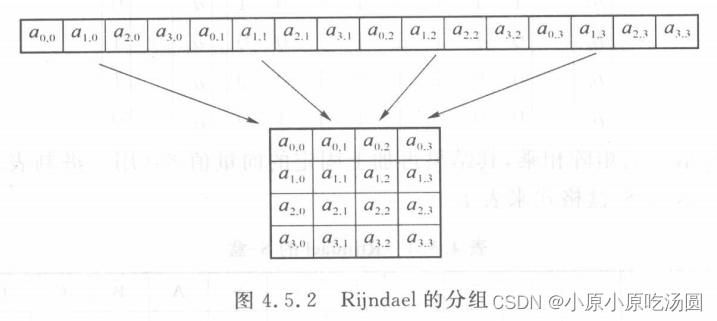
Rijndael首先将明文按字节分成列组。前4个字节组成第一列,接下来的4个字节组成第二列,依此类推,如下图所示。因为块的大小是128bit,那么就可以组成一个4×4的矩阵。
例:假设要发送的短消息为:“Bob look at this”。包括空格在内,这个消息正好为16个字节(表示成ASCII码为128bit)。
这个消息表示成十六进制为:42 6f 62 20 6c 6f 6f 6b 20 61 74 20 74 68 69 73。
写成4×4的矩阵形式为:
( 42 6 c 20 74 6 f 6 f 61 68 62 6 f 74 69 20 6 b 20 73 ) \begin{pmatrix} 42& 6c & 20 & 74\\ 6f& 6f & 61 & 68\\ 62& 6f & 74 & 69\\ 20& 6b & 20 & 73 \end{pmatrix} ⎝⎜⎜⎛426f62206c6f6f6b2061742074686973⎠⎟⎟⎞
2.AES加密操作
2.1替换操作
Rijndael使用的是一个S-盒(而不是像DES那样使用8个)。Rijndael的S-盒是一个16×16的矩阵,如下代码所示。列的每个元素作为输入用来指定S-盒的地址:前4位指定S-盒的行,后4位指定S-盒的列。由行和列所确定的S-盒位置的元素取代了明文矩阵中相应位置的元素。
//S盒
const unsigned char SBox[16][16] ={
/* 0 1 2 3 4 5 6 7 8 9 a b c d e f */
/*0*/{ 0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76 },
/*1*/{ 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0 },
/*2*/{ 0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15 },
/*3*/{ 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75 },
/*4*/{ 0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84 },
/*5*/{ 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf },
/*6*/{ 0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8 },
/*7*/{ 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2 },
/*8*/{ 0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73 },
/*9*/{ 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb },
/*a*/{ 0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79 },
/*b*/{ 0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08 },
/*c*/{ 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a },
/*d*/{ 0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e },
/*e*/{ 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf },
/*f*/{ 0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 }
};
例:上述明文的矩阵为: ( 42 6 c 20 74 6 f 6 f 61 68 62 6 f 74 69 20 6 b 20 73 ) \begin{pmatrix} 42& 6c & 20 & 74\\ 6f& 6f & 61 & 68\\ 62& 6f & 74 & 69\\ 20& 6b & 20 & 73 \end{pmatrix} ⎝⎜⎜⎛426f62206c6f6f6b2061742074686973⎠⎟⎟⎞
经过S-盒替换后变为 ( 2 c 50 b 7 92 a 8 a 8 e f 45 a a a 8 92 f 9 b 7 7 f b 7 8 f ) \begin{pmatrix} 2c & 50 & b7 & 92\\ a8 & a8 & ef & 45\\ aa & a8 & 92 & f9\\ b7 & 7f & b7 & 8f \end{pmatrix} ⎝⎜⎜⎛2ca8aab750a8a87fb7ef92b79245f98f⎠⎟⎟⎞
(0x42的前4位为0x04,后4位为0x02,在S-盒中找到对应的元素即可,其他依此类推)
S-盒替换操作的代码如下:
void SBoxFunc(unsigned char inputText[][4], unsigned char inputTextEncrypt[][4])
{
unsigned int row=0,column=0;
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
row = (inputText[i][j] & 0xF0) >> 4;
column = inputText[i][j]&0x0F;
inputTextEncrypt[i][j] = SBox[row][column];
}
}
}
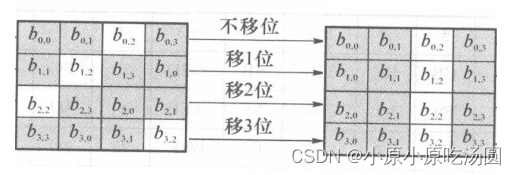
2.2行移位操作
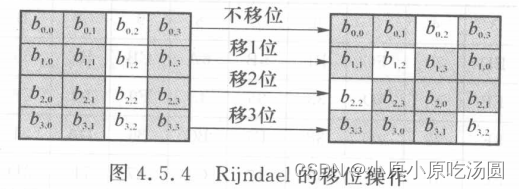
行移位操作是作用于S-盒的输出的,其中,列的4个行螺旋地左移,即第一行左移0个字节,第二行左移1个字节,第三行左移2个字节,第四行左移3个字节,如下图所示。从该图中可以看出,这使得列完全进行了重排,即在移位后的每列中,都包含有未移位前每个列的一个字节。
上述明文经S-盒变换后的矩阵为:
( 2 c 50 b 7 92 a 8 a 8 e f 45 a a a 8 92 f 9 b 7 7 f b 7 8 f ) \begin{pmatrix} 2c & 50 & b7 & 92\\ a8 & a8 & ef & 45\\ aa & a8 & 92 & f9\\ b7 & 7f & b7 & 8f \end{pmatrix} ⎝⎜⎜⎛2ca8aab750a8a87fb7ef92b79245f98f⎠⎟⎟⎞
经过行移位操作后,矩阵变为:
( 2 c 50 b 7 92 a 8 e f 45 a 8 92 f 9 a a a 8 8 f b 7 7 f b 7 ) \begin{pmatrix} 2c & 50 & b7 & 92\\ a8 & ef & 45 & a8\\ 92 & f9 & aa & a8\\ 8f & b7 & 7f & b7 \end{pmatrix} ⎝⎜⎜⎛2ca8928f50eff9b7b745aa7f92a8a8b7⎠⎟⎟⎞
行移位操作的实现代码如下所示:
//形参是一个4×4的矩阵
void ShiftRows(unsigned char inputTextEncrypt [][4])
{
unsigned char temp = 0;
for(int i=1;i<4;i++)
{
for(int j=0;j<i;j++)
{
temp = inputTextEncrypt[i][0];
inputTextEncrypt[i][0] = inputTextEncrypt[i][1];
inputTextEncrypt[i][1] = inputTextEncrypt[i][2];
inputTextEncrypt[i][2] = inputTextEncrypt[i][3];
inputTextEncrypt[i][3] = temp;
}
}
}
2.3列混合操作
列混合操作是通过矩阵相乘来实现的。经移位后的矩阵与固定的矩阵(以十六进制表示)相乘,如下所示: ( c 0 c 1 c 3 c 4 ) = ( 02 03 01 01 01 02 03 01 01 01 02 03 03 01 01 02 ) ( b 0 b 1 b 2 b 4 ) \begin{pmatrix} c_0 \\ c_1 \\ c_3 \\ c_4 \end{pmatrix} = \begin{pmatrix} 02 & 03 & 01 & 01\\ 01 & 02 & 03 & 01\\ 01 & 01 & 02 & 03\\ 03 & 01 & 01 & 02 \end{pmatrix} \begin{pmatrix} b_0 \\ b_1 \\ b_2 \\ b_4 \end{pmatrix} ⎝⎜⎜⎛c0c1c3c4⎠⎟⎟⎞=⎝⎜⎜⎛02010103030201010103020101010302⎠⎟⎟⎞⎝⎜⎜⎛b0b1b2b4⎠⎟⎟⎞
注意:这个运算需要做 G F ( 2 n ) GF(2^n) GF(2n)上的乘法,但由于所乘的因子是三个固定的元素02、03、01,所以这些乘法运算仍然是比较简单的,其中乘法运算所使用的模多项式为 m ( x ) = x 8 + x 4 + x 3 + x + 1 m(x)=x^8+x^4+x^3+x+1 m(x)=x8+x4+x3+x+1。设一个字节为 ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 ) (b_7b_6b_5b_4b_3b_2b_1b_0) (b7b6b5b4b3b2b1b0),则有:
( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 ) × ′ 0 1 ′ = ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 ) ; ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 ) × ′ 0 2 ′ = ( b 6 b 5 b 4 b 3 b 2 b 1 b 0 0 ) + ( 000 b 7 b 7 0 b 7 b 7 ) ; ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 ) × ′ 0 3 ′ = ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 ) × ′ 0 1 ′ ⊕ ( b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 ) × ′ 0 2 ′ ; (b_7b_6b_5b_4b_3b_2b_1b_0)\times '01'=(b_7b_6b_5b_4b_3b_2b_1b_0);\\ (b_7b_6b_5b_4b_3b_2b_1b_0)\times '02'=(b_6b_5b_4b_3b_2b_1b_00)+(000b_7b_70b_7b_7);\\ (b_7b_6b_5b_4b_3b_2b_1b_0)\times '03'=(b_7b_6b_5b_4b_3b_2b_1b_0)\times '01'\oplus(b_7b_6b_5b_4b_3b_2b_1b_0)\times '02'; (b7b6b5b4b3b2b1b0)×′01′=(b7b6b5b4b3b2b1b0);(b7b6b5b4b3b2b1b0)×′02′=(b6b5b4b3b2b1b00)+(000b7b70b7b7);(b7b6b5b4b3b2b1b0)×′03′=(b7b6b5b4b3b2b1b0)×′01′⊕(b7b6b5b4b3b2b1b0)×′02′;
这些操作保证了明文位经几个迭代轮后已高度打乱了,同时还保证输入与输出之间的关联很少了。这就是该算法安全性的两个重要特征。
例:上述行移位操作后的矩阵为: ( 2 c 50 b 7 92 a 8 e f 45 a 8 92 f 9 a a a 8 8 f b 7 7 f b 7 ) \begin{pmatrix} 2c & 50 & b7 & 92\\ a8 & ef & 45 & a8\\ 92 & f9 & aa & a8\\ 8f & b7 & 7f & b7 \end{pmatrix} ⎝⎜⎜⎛2ca8928f50eff9b7b745aa7f92a8a8b7⎠⎟⎟⎞
对其进行列混合,则有
( a 6 c 4 6 f c 3 45 32 a 7 8 d 31 94 3 c b 3 4 b 93 d 3 d 8 ) = ( 02 03 01 01 01 02 03 01 01 01 02 03 03 01 01 02 ) ( 2 c 50 b 7 92 a 8 e f 45 a 8 92 f 9 a a a 8 8 f b 7 7 f b 7 ) \begin{pmatrix} a6 & c4 & 6f & c3\\ 45 & 32 & a7 & 8d\\ 31 & 94 & 3c & b3\\ 4b & 93 & d3 & d8 \end{pmatrix} = \begin{pmatrix} 02 & 03 & 01 & 01\\ 01 & 02 & 03 & 01\\ 01 & 01 & 02 & 03\\ 03 & 01 & 01 & 02 \end{pmatrix} \begin{pmatrix} 2c & 50 & b7 & 92\\ a8 & ef & 45 & a8\\ 92 & f9 & aa & a8\\ 8f & b7 & 7f & b7 \end{pmatrix} ⎝⎜⎜⎛a645314bc43294936fa73cd3c38db3d8⎠⎟⎟⎞=⎝⎜⎜⎛02010103030201010103020101010302⎠⎟⎟⎞⎝⎜⎜⎛2ca8928f50eff9b7b745aa7f92a8a8b7⎠⎟⎟⎞
计算一下 ( 02 03 01 01 ) ( 2 c a 8 92 8 f ) \begin{pmatrix} 02 & 03 & 01 & 01 \end{pmatrix} \begin{pmatrix} 2c \\ a8 \\ 92 \\ 8f \end{pmatrix} (02030101)⎝⎜⎜⎛2ca8928f⎠⎟⎟⎞
02 × 2 c = 00000010 × 00101100 = 01011000 ⊕ 00000000 = 01011000 ; 03 × a 8 = 02 × a 8 ( 10101000 ) ⊕ 01 × a 8 ( 10101000 ) = 01010000 ⊕ 00011011 ⊕ 10101000 = 11100011 ; 01 × 92 = 10010010 ; 01 × 8 f = 10001111 ; 01011000 ⊕ 11100011 ⊕ 10010010 ⊕ 10001111 = 10100110 = a 6 02\times 2c=00000010\times 00101100=01011000\oplus 00000000=01011000;\\ 03\times a8=02\times a8(10101000)\oplus 01\times a8(10101000)=01010000\oplus 00011011\oplus 10101000=11100011;\\ 01\times 92=10010010;\\ 01\times8f=10001111;\\ 01011000\oplus11100011\oplus10010010\oplus10001111=10100110=a6 02×2c=00000010×00101100=01011000⊕00000000=01011000;03×a8=02×a8(10101000)⊕01×a8(10101000)=01010000⊕00011011⊕10101000=11100011;01×92=10010010;01×8f=10001111;01011000⊕11100011⊕10010010⊕10001111=10100110=a6
这样就算出了第一个值 a 6 a6 a6,其余的大家自己动手算一下就好。
注意:① ⊕ \oplus ⊕是异或操作;②乘02的时候异或的是 000 b 7 b 7 0 b 7 b 7 000b_7b_70b_7b_7 000b7b70b7b7。
列混合步骤的代码如下所示:
//要乘的矩阵
const unsigned char GFMatrix[4][4] = {
{0x02,0x03,0x01,0x01},
{0x01,0x02,0x03,0x01},
{0x01,0x01,0x02,0x03},
{0x03,0x01,0x01,0x02}
};
//下面的是矩阵相乘的操作
unsigned char GFMul01(unsigned char num)
{
return num;
}
unsigned char GFMul02(unsigned char num)
{
unsigned char temp = num>>7&0xFF;
if(temp==0x00)
return num<<1&0xFF;
else if(temp==0x01)
return (num<<1&0xFF)^0x1B;
}
unsigned char GFMul03(unsigned char num)
{
return GFMul01(num)^GFMul02(num);
}
unsigned char GFMulAll(unsigned char num1,unsigned char num2)
{
if(num2==0x01)
return GFMul01(num1);
else if(num2==0x02)
return GFMul02(num1);
else if(num2==0x03)
return GFMul03(num1);
}
//列混合实现代码
void ColumnMix(unsigned char inputTextEncrypt [][4],unsigned char inputTextColumnMix [][4])
{
for(int j=0;j<4;j++)
{
for(int i=0;i<4;i++)
{
inputTextColumnMix[i][j] = GFMulAll(inputTextEncrypt[0][j],GFMatrix[i][0])^GFMulAll(inputTextEncrypt[1][j],GFMatrix[i][1])^GFMulAll(inputTextEncrypt[2][j],GFMatrix[i][2])^GFMulAll(inputTextEncrypt[3][j],GFMatrix[i][3]);
}
}
}
2.4密钥加操作
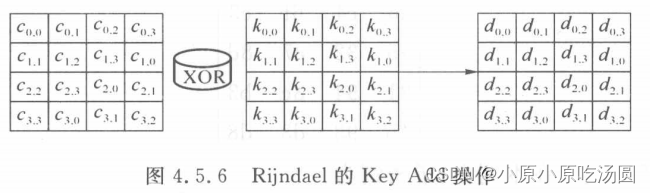
密钥加操作是每轮中的最后一个操作,是将以上结果与子密钥进行XOR逻辑运算,如下图所示。这完成了该算法的一次迭代。
例:经过列混合后,明文矩阵变为:
( a 6 c 4 6 f c 3 45 32 a 7 8 d 31 94 3 c b 3 4 b 93 d 3 d 8 ) \begin{pmatrix} a6 & c4 & 6f & c3\\ 45 & 32 & a7 & 8d\\ 31 & 94 & 3c & b3\\ 4b & 93 & d3 & d8 \end{pmatrix} ⎝⎜⎜⎛a645314bc43294936fa73cd3c38db3d8⎠⎟⎟⎞
假设此时的轮密钥为:
( 01 a 3 90 12 e 1 44 20 11 c c 73 04 a 9 59 06 30 b 4 ) \begin{pmatrix} 01 & a3 & 90 & 12\\ e1 & 44 & 20 & 11\\ cc & 73 & 04 & a9\\ 59 & 06 & 30 & b4 \end{pmatrix} ⎝⎜⎜⎛01e1cc59a3447306902004301211a9b4⎠⎟⎟⎞
则有
( a 6 c 4 6 f c 3 45 32 a 7 8 d 31 94 3 c b 3 4 b 93 d 3 d 8 ) X O R ( 01 a 3 90 12 e 1 44 20 11 c c 73 04 a 9 59 06 30 b 4 ) = ( a 7 67 f f d 1 a 4 76 87 9 c f d e 7 38 1 a 12 95 e 3 6 c ) \begin{pmatrix} a6 & c4 & 6f & c3\\ 45 & 32 & a7 & 8d\\ 31 & 94 & 3c & b3\\ 4b & 93 & d3 & d8 \end{pmatrix} XOR \begin{pmatrix} 01 & a3 & 90 & 12\\ e1 & 44 & 20 & 11\\ cc & 73 & 04 & a9\\ 59 & 06 & 30 & b4 \end{pmatrix} = \begin{pmatrix} a7 & 67 & ff & d1\\ a4 & 76 & 87 & 9c\\ fd & e7 & 38 & 1a\\ 12 & 95 & e3 & 6c \end{pmatrix} ⎝⎜⎜⎛a645314bc43294936fa73cd3c38db3d8⎠⎟⎟⎞XOR⎝⎜⎜⎛01e1cc59a3447306902004301211a9b4⎠⎟⎟⎞=⎝⎜⎜⎛a7a4fd126776e795ff8738e3d19c1a6c⎠⎟⎟⎞
a 6 ⊕ 01 = a 7 ; c 4 ⊕ a 3 = 67 ; a6\oplus01=a7;c4\oplus a3=67; a6⊕01=a7;c4⊕a3=67;依此类推
密钥加操作的代码如下:
void RoundKeyXOR(unsigned char inputTextColumnMix [][4],unsigned char RoundKey [][4],unsigned char inputText[][4])
{
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
inputText[i][j] = inputTextColumnMix[i][j]^RoundKey[i][j];
}
}
}
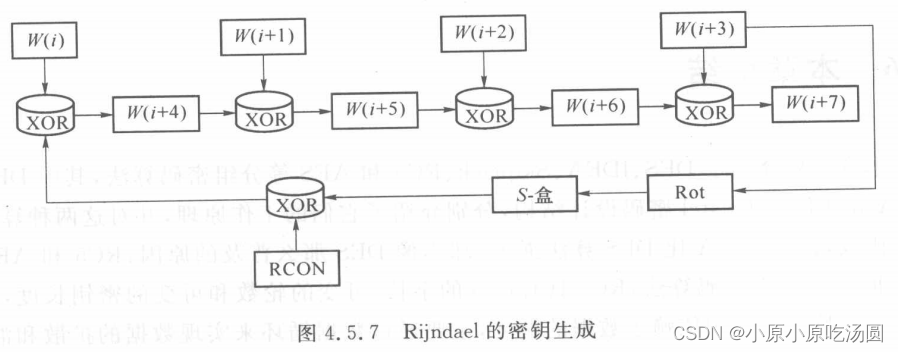
3.AES的密钥生成
密钥是按矩阵的列进行分组的,然后添加40个新列来进行扩充。如果前4列(即由密钥给定的那些列)为 W ( 0 ) W(0) W(0)、 W ( 1 ) W(1) W(1)、 W ( 2 ) W(2) W(2)和 W ( 3 ) W(3) W(3),那么新列以递归方式产生。
如果 i i i不是4的倍数,那么第 i i i列由如下等式确定: W ( i ) = W ( i − 4 ) X O R W ( i − 1 ) W(i)=W(i-4) \quad XOR \quad W(i-1) W(i)=W(i−4)XORW(i−1)如果 i i i是4的倍数,那么第 i i i列由如下等式确定: W ( i ) = W ( i − 4 ) X O R T [ W ( i − 1 ) ] W(i)=W(i-4) \quad XOR \quad T[W(i-1)] W(i)=W(i−4)XORT[W(i−1)]其中 T [ W ( i − 1 ) ] T[W(i-1)] T[W(i−1)]是 W ( i − 1 ) W(i-1) W(i−1)的一种转换形式,按一下方式实现的:
(1)循环地将 W ( i − 1 ) W(i-1) W(i−1)的元素移位,每次一个字节,也就是说, a b c d abcd abcd变成 b c d a bcda bcda(一个字母是一个字节大小)。
(2)将这4个字节作为S-盒的输入,输出新的4个字节 e f g h efgh efgh。
(3)计算一轮的常量 r ( i ) = 2 ( i − 4 ) / 4 r(i)=2^{(i-4)/4} r(i)=2(i−4)/4。
(4)这样生成转换后的列: [ e X O R r ( i ) , f , g , h ] [e\quad XOR \quad r(i),f,g,h] [eXORr(i),f,g,h]。
第 i i i轮的轮密钥组成了列 W ( 4 i ) W(4i) W(4i)、 W ( 4 i + 1 ) W(4i+1) W(4i+1)、 W ( 4 i + 2 ) W(4i+2) W(4i+2)和 W ( 4 i + 3 ) W(4i+3) W(4i+3)。过程如下图所示:
例:如果初始的128bit密钥为(以十六进制表示):3ca10b21、57f01916、902e1380和acc107bd。
那么4个初始值为 W ( 0 ) = 3 c a 10 b 21 , W ( 1 ) = 57 f 01916 , W ( 2 ) = 902 e 1380 , W ( 3 ) = a c c 107 b d W(0)=3ca10b21,W(1)=57f01916,W(2)=902e1380,W(3)=acc107bd W(0)=3ca10b21,W(1)=57f01916,W(2)=902e1380,W(3)=acc107bd。
即 ( 3 c 57 90 a c a 1 f 0 2 e c 1 0 b 19 13 07 21 16 80 b d ) \begin{pmatrix} 3c & 57 & 90 & ac\\ a1 & f0 & 2e & c1\\ 0b & 19 & 13 & 07\\ 21 & 16 & 80 & bd \end{pmatrix} ⎝⎜⎜⎛3ca10b2157f01916902e1380acc107bd⎠⎟⎟⎞下一个子密钥段为 W ( 4 ) W(4) W(4),由于4是4的倍数,所以 W ( 4 ) = W ( 0 ) X O R T [ W ( 3 ) ] W(4)=W(0) \quad XOR \quad T[W(3)] W(4)=W(0)XORT[W(3)] T [ W ( 3 ) ] T[W(3)] T[W(3)]的计算步骤如下:
(1)循环地将 W ( 3 ) W(3) W(3)的元素移位: a c c 107 b d acc107bd acc107bd变成了 c 107 b d a c c107bdac c107bdac。
(2)将 c 107 b d a c c107bdac c107bdac作为S-盒的输入,输出 78857 a 91 78857a91 78857a91。
(3)计算一轮的常量 r ( 4 ) = 2 0 = 01 r(4)=2^0=01 r(4)=20=01(以十六进制表示)。
(4)将 r ( 4 ) r(4) r(4)与第一个字节78进行XOR逻辑运算: 78 X O R 01 = 79 78\quad XOR \quad 01=79 78XOR01=79。
因此, T [ W ( 3 ) ] = 79857 a 91 T[W(3)]=79857a91 T[W(3)]=79857a91,并且 W ( 4 ) = 3 c a 10 b 21 X O R 79857 a 91 = 456471 b 0 W(4)=3ca10b21\quad XOR \quad 79857a91=456471b0 W(4)=3ca10b21XOR79857a91=456471b0
其余的3个子密钥段计算如下: W ( 5 ) = W ( 1 ) X O R W ( 4 ) = 57 f 01916 X O R 456471 b 0 = 129468 a 6 ; W(5)=W(1) \quad XOR \quad W(4)=57f01916\quad XOR \quad 456471b0=129468a6; W(5)=W(1)XORW(4)=57f01916XOR456471b0=129468a6; W ( 6 ) = W ( 2 ) X O R W ( 5 ) = 902 c 1380 X O R 129468 a 6 = 82 b 87 b 26 ; W(6)=W(2) \quad XOR \quad W(5)=902c1380 \quad XOR \quad 129468a6=82b87b26; W(6)=W(2)XORW(5)=902c1380XOR129468a6=82b87b26; W ( 7 ) = W ( 3 ) X O R W ( 6 ) = a c c 107 b d X O R 82 b 87 b 26 = 2 e 797 c 9 b ; W(7)=W(3) \quad XOR \quad W(6)=acc107bd \quad XOR \quad 82b87b26=2e797c9b; W(7)=W(3)XORW(6)=acc107bdXOR82b87b26=2e797c9b;
于是,第一轮的密钥为: 456471 b 0 129468 a 6 82 b 87 b 26 2 e 797 c 9 b 456471b0\quad129468a6\quad82b87b26\quad2e797c9b 456471b0129468a682b87b262e797c9b。
AES密钥生成的代码如下:
//循环中常量r的值
const unsigned char R[10] = {0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80,0x1B,0x36};
//密钥生成的过程
void CipherKeyExtended(unsigned char cipherKey[][4] , unsigned char cipherKeySum[][44])
{
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
cipherKeySum[i][j] = cipherKey[i][j];
}
}
unsigned char tempColumnLast[4] = {0};
for(int j=4;j<44;j++)
{
if(j%4!=0)
{
for(int i=0;i<4;i++)
{
cipherKeySum[i][j] = cipherKeySum[i][j-4]^cipherKeySum[i][j-1];
}
}
else
{
for(int i=0;i<4;i++)
{
tempColumnLast[i] = cipherKeySum[i][j-1];
}
unsigned char temp = tempColumnLast[0];
for(int k=0;k<3;k++)
{
tempColumnLast[k] = tempColumnLast[k+1];
}
tempColumnLast[3] = temp;
for(int k=0;k<4;k++)
{
tempColumnLast[k] = SBox[(tempColumnLast[k]&0xF0)>>4][tempColumnLast[k]&0x0F];
}
tempColumnLast[0] = tempColumnLast[0]^R[j/4-1];
for(int i=0;i<4;i++)
{
cipherKeySum[i][j] = cipherKeySum[i][j-4]^tempColumnLast[i];
}
}
}
}
4.AES解密操作
4.1逆行移位
行移位操作是列的4个行螺旋地左移,则逆行移位操作就是列的4个行螺旋地右移,即第一行右移0个字节,第二行右移1个字节,第三行右移2个字节,第四行右移3个字节,如下图所示。
例:假设有一个矩阵为: ( 1 d d c d 4 07 18 43 22 2 b f 6 40 10 25 65 47 2 f a f ) \begin{pmatrix} 1d & dc & d4 & 07\\ 18 & 43 & 22 & 2b\\ f6 & 40 & 10 & 25\\ 65 & 47 & 2f & af \end{pmatrix} ⎝⎜⎜⎛1d18f665dc434047d422102f072b25af⎠⎟⎟⎞对其进行逆行移位操作,则得到矩阵: ( 1 d d c d 4 07 2 b 18 43 22 10 25 f 6 40 47 2 f a f 65 ) \begin{pmatrix} 1d & dc & d4 & 07\\ 2b & 18 & 43 & 22\\ 10 & 25 & f6 & 40\\ 47 & 2f & af & 65 \end{pmatrix} ⎝⎜⎜⎛1d2b1047dc18252fd443f6af07224065⎠⎟⎟⎞
逆行移位操作的代码如下:
void ReShiftRows(unsigned char inputTextEncrypt [][4])
{
unsigned char temp = 0;
for(int i=1;i<4;i++)
{
for(int j=0;j<i;j++)
{
temp = inputTextEncrypt[i][3];
inputTextEncrypt[i][3] = inputTextEncrypt[i][2];
inputTextEncrypt[i][2] = inputTextEncrypt[i][1];
inputTextEncrypt[i][1] = inputTextEncrypt[i][0];
inputTextEncrypt[i][0] = temp;
}
}
}
4.2逆S-盒替换
逆S-盒替换使用的S-盒也是一个 16 × 16 16\times16 16×16的矩阵,如下代码所示。列的每个元素作为输入用来指定S-盒的地址:前4位指定S-盒的行,后4位指定S-盒的列。由行和列所确定的S-盒位置的元素取代了密文矩阵中相应位置的元素。
//逆S盒
const unsigned char ReSBox[16][16] = {
/* 0 1 2 3 4 5 6 7 8 9 a b c d e f */
{0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb},
{0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb},
{0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e},
{0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25},
{0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92},
{0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84},
{0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06},
{0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b},
{0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73},
{0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e},
{0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b},
{0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4},
{0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f},
{0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef},
{0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61},
{0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d}
};
例:假设密文矩阵为: ( 2 c 50 b 7 92 a 8 a 8 e f 45 a a a 8 92 f 9 b 7 7 f b 7 8 f ) \begin{pmatrix} 2c & 50 & b7 & 92\\ a8 & a8 & ef & 45\\ aa & a8 & 92 & f9\\ b7 & 7f & b7 & 8f \end{pmatrix} ⎝⎜⎜⎛2ca8aab750a8a87fb7ef92b79245f98f⎠⎟⎟⎞经过逆S-盒替换操作后,矩阵变为: ( 42 6 c 20 74 6 f 6 f 61 68 62 6 f 74 69 20 6 b 20 73 ) \begin{pmatrix} 42& 6c & 20 & 74\\ 6f& 6f & 61 & 68\\ 62& 6f & 74 & 69\\ 20& 6b & 20 & 73 \end{pmatrix} ⎝⎜⎜⎛426f62206c6f6f6b2061742074686973⎠⎟⎟⎞
逆S-盒替换操作的代码如下:
void ReSBoxFunc(unsigned char inputText[][4],unsigned char inputTextEncrypt[][4])
{
unsigned int row=0,column=0;
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
row = (inputText[i][j] & 0xF0) >> 4;
column = inputText[i][j]&0x0F;
inputTextEncrypt[i][j] = ReSBox[row][column];
}
}
}
4.3密钥加操作
解密时执行的密钥加操作和加密时采用的密钥加操作是相同的,注意加密和解密使用的是同一组轮密钥即可。
4.4逆列混合操作
逆列混合操作是通过矩阵相乘来实现的。将密文矩阵与固定的矩阵(以十六进制表示)相乘,如下所示。 ( c 0 c 1 c 2 c 3 ) = ( 0 E 0 B 0 D 09 09 0 E 0 B 0 D 0 D 09 0 E 0 B 0 B 0 D 09 0 E ) ( b 0 b 1 b 2 b 3 ) \begin{pmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \end{pmatrix} = \begin{pmatrix} 0E & 0B & 0D & 09\\ 09 & 0E & 0B & 0D\\ 0D & 09 & 0E & 0B\\ 0B & 0D & 09 & 0E \end{pmatrix} \begin{pmatrix} b_0 \\ b_1 \\ b_2 \\ b_3 \end{pmatrix} ⎝⎜⎜⎛c0c1c2c3⎠⎟⎟⎞=⎝⎜⎜⎛0E090D0B0B0E090D0D0B0E09090D0B0E⎠⎟⎟⎞⎝⎜⎜⎛b0b1b2b3⎠⎟⎟⎞下面介绍如何进行相乘。
假设存在一个字节 B B B,则有:
B × ′ 0 9 ′ = B × ( ′ 0 8 ′ ⊕ ′ 0 1 ′ ) = ( B × ′ 0 2 ′ × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( B × ′ 0 1 ′ ) ; B × ′ 0 B ′ = B × ( ′ 0 8 ′ ⊕ ′ 0 2 ′ ⊕ ′ 0 1 ′ ) = ( B × ′ 0 2 ′ × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( B × ′ 0 2 ′ ) ⊕ ( B × ′ 0 1 ′ ) ; B × ′ 0 D ′ = B × ( ′ 0 8 ′ ⊕ ′ 0 4 ′ ⊕ ′ 0 1 ′ ) = ( B × ′ 0 2 ′ × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( B × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( B × ′ 0 1 ′ ) ; B × ′ 0 E ′ = B × ( ′ 0 8 ′ ⊕ ′ 0 4 ′ ⊕ ′ 0 2 ′ ) = ( B × ′ 0 2 ′ × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( B × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( B × ′ 0 2 ′ ) ; B\times '09'=B\times ('08'\oplus '01')=(B\times'02'\times '02'\times '02')\oplus (B\times '01');\\ B\times '0B'=B\times ('08'\oplus '02'\oplus '01')=(B\times'02'\times '02'\times '02')\oplus (B\times'02')\oplus (B\times '01');\\ B\times '0D'=B\times ('08'\oplus '04'\oplus '01')=(B\times'02'\times '02'\times '02')\oplus (B\times'02'\times '02')\oplus (B\times '01');\\ B\times '0E'=B\times ('08'\oplus '04'\oplus '02')=(B\times'02'\times '02'\times '02')\oplus (B\times'02'\times '02')\oplus (B\times '02');\\ B×′09′=B×(′08′⊕′01′)=(B×′02′×′02′×′02′)⊕(B×′01′);B×′0B′=B×(′08′⊕′02′⊕′01′)=(B×′02′×′02′×′02′)⊕(B×′02′)⊕(B×′01′);B×′0D′=B×(′08′⊕′04′⊕′01′)=(B×′02′×′02′×′02′)⊕(B×′02′×′02′)⊕(B×′01′);B×′0E′=B×(′08′⊕′04′⊕′02′)=(B×′02′×′02′×′02′)⊕(B×′02′×′02′)⊕(B×′02′);
例:假设密文矩阵为: ( 60 65 67 63 79 e 7 f 9 00 46 a 3 7 e 52 74 c c 13 98 ) \begin{pmatrix} 60 & 65 & 67 & 63\\ 79 & e7 & f9 & 00\\ 46 & a3 & 7e & 52\\ 74 & cc & 13 & 98 \end{pmatrix} ⎝⎜⎜⎛6079467465e7a3cc67f97e1363005298⎠⎟⎟⎞经过逆列混合操作后,得: ( a 2 8 b 0 e f 7 5 b 07 43 64 d 2 8 c e a 8 f 00 e d 54 b 5 ) = ( 0 E 0 B 0 D 09 09 0 E 0 B 0 D 0 D 09 0 E 0 B 0 B 0 D 09 0 E ) ( 60 65 67 63 79 e 7 f 9 00 46 a 3 7 e 52 74 c c 13 98 ) \begin{pmatrix} a2 & 8b & 0e & f7\\ 5b & 07 & 43 & 64\\ d2 & 8c & ea & 8f\\ 00 & ed & 54 & b5 \end{pmatrix} = \begin{pmatrix} 0E & 0B & 0D & 09\\ 09 & 0E & 0B & 0D\\ 0D & 09 & 0E & 0B\\ 0B & 0D & 09 & 0E \end{pmatrix} \begin{pmatrix} 60 & 65 & 67 & 63\\ 79 & e7 & f9 & 00\\ 46 & a3 & 7e & 52\\ 74 & cc & 13 & 98 \end{pmatrix} ⎝⎜⎜⎛a25bd2008b078ced0e43ea54f7648fb5⎠⎟⎟⎞=⎝⎜⎜⎛0E090D0B0B0E090D0D0B0E09090D0B0E⎠⎟⎟⎞⎝⎜⎜⎛6079467465e7a3cc67f97e1363005298⎠⎟⎟⎞下面计算: ( 0 E 0 B 0 D 09 ) ( 60 79 46 74 ) \begin{pmatrix} 0E & 0B & 0D & 09 \end{pmatrix} \begin{pmatrix} 60 \\ 79 \\ 46 \\ 74 \end{pmatrix} (0E0B0D09)⎝⎜⎜⎛60794674⎠⎟⎟⎞
60 × ′ 0 E ′ = ( 01100000 × ′ 0 2 ′ × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 01100000 × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 01100000 × ′ 0 2 ′ ) = ( 11000000 × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 11000000 × ′ 0 2 ′ ) ⊕ ( 11000000 ) = ( 10011011 × ′ 0 2 ′ ) ⊕ ( 10011011 ) ⊕ ( 11000000 ) = ( 00101101 ) ⊕ ( 10011011 ) ⊕ ( 11000000 ) = 01110110 60\times '0E'=(01100000\times '02'\times '02'\times '02')\oplus (01100000\times '02'\times '02')\oplus(01100000\times '02')\\ =(11000000\times '02'\times '02')\oplus (11000000\times '02') \oplus (11000000)\\ =(10011011\times '02')\oplus (10011011)\oplus (11000000)\\ =(00101101)\oplus (10011011)\oplus (11000000)=01110110 60×′0E′=(01100000×′02′×′02′×′02′)⊕(01100000×′02′×′02′)⊕(01100000×′02′)=(11000000×′02′×′02′)⊕(11000000×′02′)⊕(11000000)=(10011011×′02′)⊕(10011011)⊕(11000000)=(00101101)⊕(10011011)⊕(11000000)=01110110
79 × ′ 0 B ′ = ( 01111001 × ′ 0 2 ′ × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 01111001 × ′ 0 2 ′ ) ⊕ ( 01111001 × ′ 0 1 ′ ) = ( 11110010 × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 11110010 ) ⊕ ( 01111001 ) = ( 11111111 × ′ 0 2 ′ ) ⊕ ( 11110010 ) ⊕ ( 01111001 ) = ( 11100101 ) ⊕ ( 11110010 ) ⊕ ( 01111001 ) = 01101110 79\times '0B'=(01111001\times '02'\times '02'\times '02')\oplus (01111001\times '02')\oplus (01111001\times '01')\\ =(11110010\times '02'\times '02')\oplus (11110010)\oplus (01111001)\\ =(11111111\times '02')\oplus (11110010)\oplus (01111001)\\ =(11100101)\oplus (11110010)\oplus (01111001)=01101110 79×′0B′=(01111001×′02′×′02′×′02′)⊕(01111001×′02′)⊕(01111001×′01′)=(11110010×′02′×′02′)⊕(11110010)⊕(01111001)=(11111111×′02′)⊕(11110010)⊕(01111001)=(11100101)⊕(11110010)⊕(01111001)=01101110
46 × ′ 0 D ′ = ( 01000110 × ′ 0 2 ′ × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 01000110 × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 01000110 × ′ 0 1 ′ ) = ( 10001100 × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 10001100 × ′ 0 2 ′ ) ⊕ ( 01000110 ) = ( 00000011 × ′ 0 2 ′ ) ⊕ ( 00000011 ) ⊕ ( 01000110 ) = ( 00000110 ) ⊕ ( 00000011 ) ⊕ ( 01000110 ) = 01000011 46\times '0D'=(01000110\times '02'\times '02'\times '02')\oplus (01000110\times '02'\times '02')\oplus (01000110\times '01')\\ =(10001100\times '02'\times '02')\oplus(10001100\times '02')\oplus (01000110)\\ =(00000011\times '02')\oplus (00000011)\oplus (01000110)\\ =(00000110)\oplus (00000011)\oplus (01000110)=01000011 46×′0D′=(01000110×′02′×′02′×′02′)⊕(01000110×′02′×′02′)⊕(01000110×′01′)=(10001100×′02′×′02′)⊕(10001100×′02′)⊕(01000110)=(00000011×′02′)⊕(00000011)⊕(01000110)=(00000110)⊕(00000011)⊕(01000110)=01000011
74 × ′ 0 9 ′ = ( 01110100 × ′ 0 2 ′ × ′ 0 2 ′ × ′ 0 2 ′ ) ⊕ ( 01110100 × ′ 0 1 ′ ) = ( 11101000 × ′ 0 2 ′ ) ⊕ ( 01110100 ) = ( 11001011 × ′ 0 2 ′ ) ⊕ ( 01110100 ) = ( 10001101 ) ⊕ ( 01110100 ) = 11111001 74\times '09'=(01110100\times '02'\times '02'\times '02')\oplus (01110100\times '01')\\ =(11101000\times '02')\oplus (01110100)\\ =(11001011\times '02')\oplus (01110100)\\ =(10001101)\oplus (01110100)=11111001 74×′09′=(01110100×′02′×′02′×′02′)⊕(01110100×′01′)=(11101000×′02′)⊕(01110100)=(11001011×′02′)⊕(01110100)=(10001101)⊕(01110100)=11111001
01110110 ⊕ 01101110 ⊕ 01000011 ⊕ 11111001 = 10100010 = a 2 01110110\oplus01101110\oplus01000011\oplus11111001=10100010=a2 01110110⊕01101110⊕01000011⊕11111001=10100010=a2
逆列混合的代码如下:
unsigned char GFMul04(unsigned char num)
{
unsigned char temp=num;
for(int i=0;i<2;i++)
{
temp = GFMul02(temp);
}
return temp;
}
unsigned char GFMul08(unsigned char num)
{
unsigned char temp=num;
for(int i=0;i<3;i++)
{
temp = GFMul02(temp);
}
return temp;
}
unsigned char GFMul09(unsigned char num)
{
return GFMul08(num)^GFMul01(num);
}
unsigned char GFMul0B(unsigned char num)
{
return GFMul08(num)^GFMul02(num)^GFMul01(num);
}
unsigned char GFMul0D(unsigned char num)
{
return GFMul08(num)^GFMul04(num)^GFMul01(num);
}
unsigned char GFMul0E(unsigned char num)
{
return GFMul08(num)^GFMul04(num)^GFMul02(num);
}
unsigned char ReGFMulAll(unsigned char num1,unsigned char num2)
{
if(num2==0x09)
return GFMul09(num1);
else if(num2==0x0B)
return GFMul0B(num1);
else if(num2==0x0D)
return GFMul0D(num1);
else if(num2==0x0E)
return GFMul0E(num1);
}
void ReColumnMix(unsigned char inputTextColumnMix [][4],unsigned char inputTextEncrypt [][4])
{
for(int j=0;j<4;j++)
{
for(int i=0;i<4;i++)
{
inputTextEncrypt[i][j] = ReGFMulAll(inputTextColumnMix[0][j],ReGFMatrix[i][0])^ReGFMulAll(inputTextColumnMix[1][j],ReGFMatrix[i][1])^ReGFMulAll(inputTextColumnMix[2][j],ReGFMatrix[i][2])^ReGFMulAll(inputTextColumnMix[3][j],ReGFMatrix[i][3]);
}
}
}
5.完整代码
//aes.h
#ifndef _AES_H_
#define _AES_H_
#include<stdio.h>
//S盒
const unsigned char SBox[16][16] ={
/* 0 1 2 3 4 5 6 7 8 9 a b c d e f */
/*0*/{ 0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76 },
/*1*/{ 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0 },
/*2*/{ 0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15 },
/*3*/{ 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75 },
/*4*/{ 0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84 },
/*5*/{ 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf },
/*6*/{ 0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8 },
/*7*/{ 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2 },
/*8*/{ 0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73 },
/*9*/{ 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb },
/*a*/{ 0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79 },
/*b*/{ 0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08 },
/*c*/{ 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a },
/*d*/{ 0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e },
/*e*/{ 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf },
/*f*/{ 0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 }
};
//逆S盒
const unsigned char ReSBox[16][16] = {
/* 0 1 2 3 4 5 6 7 8 9 a b c d e f */
{0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb},
{0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb},
{0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e},
{0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25},
{0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92},
{0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84},
{0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06},
{0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b},
{0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73},
{0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e},
{0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b},
{0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4},
{0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f},
{0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef},
{0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61},
{0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d}
};
const unsigned char GFMatrix[4][4] = {
{0x02,0x03,0x01,0x01},
{0x01,0x02,0x03,0x01},
{0x01,0x01,0x02,0x03},
{0x03,0x01,0x01,0x02}
};
const unsigned char ReGFMatrix[4][4] = {
{0x0E,0x0B,0x0D,0x09},
{0x09,0x0E,0x0B,0x0D},
{0x0D,0x09,0x0E,0x0B},
{0x0B,0x0D,0x09,0x0E}
};
const unsigned char R[10] = {0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80,0x1B,0x36};
#endif
#include "aes.h"
//S盒置换
void SBoxFunc(unsigned char inputText[][4], unsigned char inputTextEncrypt[][4]);
//S盒逆置换
void ReSBoxFunc(unsigned char inputText[][4],unsigned char inputTextEncrypt[][4]);
//行移位
void ShiftRows(unsigned char inputTextEncrypt [][4]);
//逆行移位
void ReShiftRows(unsigned char inputTextEncrypt [][4]);
//列混合
unsigned char GFMul01(unsigned char num);
unsigned char GFMul02(unsigned char num);
unsigned char GFMul03(unsigned char num);
unsigned char GFMulAll(unsigned char num1,unsigned char num2);
void ColumnMix(unsigned char inputTextEncrypt [][4],unsigned char inputTextColumnMix [][4]);
//逆列混合
unsigned char GFMul04(unsigned char num);
unsigned char GFMul08(unsigned char num);
unsigned char GFMul09(unsigned char num);
unsigned char GFMul0B(unsigned char num);
unsigned char GFMul0D(unsigned char num);
unsigned char GFMul0E(unsigned char num);
unsigned char ReGFMulAll(unsigned char num1,unsigned char num2);
void ReColumnMix(unsigned char inputTextColumnMix [][4],unsigned char inputTextEncrypt [][4]);
//轮密钥异或
void RoundKeyXOR(unsigned char inputTextColumnMix [][4],unsigned char RoundKey [][4],unsigned char inputText[][4]);
//密钥扩展
void CipherKeyExtended(unsigned char cipherKey[][4] , unsigned char cipherKeySum[][44]);
//加密
void Encrypt(unsigned char inputText[][4],unsigned char cipherKeySum[][44]);
//解密
void Decrypt(unsigned char inputText[][4],unsigned char cipherKeySum[][44]);
//对4*4矩阵进行打印
void printMatrix(unsigned char matrix[][4]);
void printMatrix(unsigned char matrix[][4])
{
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
printf("%.2x ",matrix[i][j]);
}
printf("\n");
}
}
void SBoxFunc(unsigned char inputText[][4], unsigned char inputTextEncrypt[][4])
{
unsigned int row=0,column=0;
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
row = (inputText[i][j] & 0xF0) >> 4;
column = inputText[i][j]&0x0F;
inputTextEncrypt[i][j] = SBox[row][column];
}
}
}
void ReSBoxFunc(unsigned char inputText[][4],unsigned char inputTextEncrypt[][4])
{
unsigned int row=0,column=0;
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
row = (inputText[i][j] & 0xF0) >> 4;
column = inputText[i][j]&0x0F;
inputTextEncrypt[i][j] = ReSBox[row][column];
}
}
}
void ShiftRows(unsigned char inputTextEncrypt [][4])
{
unsigned char temp = 0;
for(int i=1;i<4;i++)
{
for(int j=0;j<i;j++)
{
temp = inputTextEncrypt[i][0];
inputTextEncrypt[i][0] = inputTextEncrypt[i][1];
inputTextEncrypt[i][1] = inputTextEncrypt[i][2];
inputTextEncrypt[i][2] = inputTextEncrypt[i][3];
inputTextEncrypt[i][3] = temp;
}
}
}
void ReShiftRows(unsigned char inputTextEncrypt [][4])
{
unsigned char temp = 0;
for(int i=1;i<4;i++)
{
for(int j=0;j<i;j++)
{
temp = inputTextEncrypt[i][3];
inputTextEncrypt[i][3] = inputTextEncrypt[i][2];
inputTextEncrypt[i][2] = inputTextEncrypt[i][1];
inputTextEncrypt[i][1] = inputTextEncrypt[i][0];
inputTextEncrypt[i][0] = temp;
}
}
}
unsigned char GFMul01(unsigned char num)
{
return num;
}
unsigned char GFMul02(unsigned char num)
{
unsigned char temp = num>>7&0xFF;
if(temp==0x00)
return num<<1&0xFF;
else if(temp==0x01)
return (num<<1&0xFF)^0x1B;
}
unsigned char GFMul03(unsigned char num)
{
return GFMul01(num)^GFMul02(num);
}
unsigned char GFMulAll(unsigned char num1,unsigned char num2)
{
if(num2==0x01)
return GFMul01(num1);
else if(num2==0x02)
return GFMul02(num1);
else if(num2==0x03)
return GFMul03(num1);
}
void ColumnMix(unsigned char inputTextEncrypt [][4],unsigned char inputTextColumnMix [][4])
{
for(int j=0;j<4;j++)
{
for(int i=0;i<4;i++)
{
inputTextColumnMix[i][j] = GFMulAll(inputTextEncrypt[0][j],GFMatrix[i][0])^GFMulAll(inputTextEncrypt[1][j],GFMatrix[i][1])^GFMulAll(inputTextEncrypt[2][j],GFMatrix[i][2])^GFMulAll(inputTextEncrypt[3][j],GFMatrix[i][3]);
}
}
}
unsigned char GFMul04(unsigned char num)
{
unsigned char temp=num;
for(int i=0;i<2;i++)
{
temp = GFMul02(temp);
}
return temp;
}
unsigned char GFMul08(unsigned char num)
{
unsigned char temp=num;
for(int i=0;i<3;i++)
{
temp = GFMul02(temp);
}
return temp;
}
unsigned char GFMul09(unsigned char num)
{
return GFMul08(num)^GFMul01(num);
}
unsigned char GFMul0B(unsigned char num)
{
return GFMul08(num)^GFMul02(num)^GFMul01(num);
}
unsigned char GFMul0D(unsigned char num)
{
return GFMul08(num)^GFMul04(num)^GFMul01(num);
}
unsigned char GFMul0E(unsigned char num)
{
return GFMul08(num)^GFMul04(num)^GFMul02(num);
}
unsigned char ReGFMulAll(unsigned char num1,unsigned char num2)
{
if(num2==0x09)
return GFMul09(num1);
else if(num2==0x0B)
return GFMul0B(num1);
else if(num2==0x0D)
return GFMul0D(num1);
else if(num2==0x0E)
return GFMul0E(num1);
}
void ReColumnMix(unsigned char inputTextColumnMix [][4],unsigned char inputTextEncrypt [][4])
{
for(int j=0;j<4;j++)
{
for(int i=0;i<4;i++)
{
inputTextEncrypt[i][j] = ReGFMulAll(inputTextColumnMix[0][j],ReGFMatrix[i][0])^ReGFMulAll(inputTextColumnMix[1][j],ReGFMatrix[i][1])^ReGFMulAll(inputTextColumnMix[2][j],ReGFMatrix[i][2])^ReGFMulAll(inputTextColumnMix[3][j],ReGFMatrix[i][3]);
}
}
}
void RoundKeyXOR(unsigned char inputTextColumnMix [][4],unsigned char RoundKey [][4],unsigned char inputText[][4])
{
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
inputText[i][j] = inputTextColumnMix[i][j]^RoundKey[i][j];
}
}
}
void CipherKeyExtended(unsigned char cipherKey[][4] , unsigned char cipherKeySum[][44])
{
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
cipherKeySum[i][j] = cipherKey[i][j];
}
}
unsigned char tempColumnLast[4] = {0};
for(int j=4;j<44;j++)
{
if(j%4!=0)
{
for(int i=0;i<4;i++)
{
cipherKeySum[i][j] = cipherKeySum[i][j-4]^cipherKeySum[i][j-1];
}
}
else
{
for(int i=0;i<4;i++)
{
tempColumnLast[i] = cipherKeySum[i][j-1];
}
unsigned char temp = tempColumnLast[0];
for(int k=0;k<3;k++)
{
tempColumnLast[k] = tempColumnLast[k+1];
}
tempColumnLast[3] = temp;
for(int k=0;k<4;k++)
{
tempColumnLast[k] = SBox[(tempColumnLast[k]&0xF0)>>4][tempColumnLast[k]&0x0F];
}
tempColumnLast[0] = tempColumnLast[0]^R[j/4-1];
for(int i=0;i<4;i++)
{
cipherKeySum[i][j] = cipherKeySum[i][j-4]^tempColumnLast[i];
}
}
}
}
void Encrypt(unsigned char inputText[][4],unsigned char cipherKeySum[][44])
{
unsigned char inputTextEncrypt[4][4] = {0};
unsigned char inputTextColumnMix[4][4] = {0};
unsigned char cipherKey[4][4] = {0};
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
cipherKey[i][j] = cipherKeySum[i][j];
}
}
RoundKeyXOR(inputText,cipherKey,inputText);
for(int i=1;i<=9;i++)
{
for(int m=0;m<4;m++)
{
for(int n=0;n<4;n++)
{
cipherKey[m][n] = cipherKeySum[m][4*i+n];
}
}
SBoxFunc(inputText,inputTextEncrypt);
ShiftRows(inputTextEncrypt);
ColumnMix(inputTextEncrypt,inputTextColumnMix);
RoundKeyXOR(inputTextColumnMix,cipherKey,inputText);
}
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
cipherKey[i][j] = cipherKeySum[i][40+j];
}
}
SBoxFunc(inputText,inputTextEncrypt);
ShiftRows(inputTextEncrypt);
RoundKeyXOR(inputTextEncrypt,cipherKey,inputText);
}
void Decrypt(unsigned char inputText[][4],unsigned char cipherKeySum[][44])
{
unsigned char reInputTextEncrypt[4][4] = {0};
unsigned char reInputTextRoundKeyXOR[4][4] = {0};
unsigned char cipherKey[4][4] = {0};
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
cipherKey[i][j] = cipherKeySum[i][40+j];
}
}
RoundKeyXOR(inputText,cipherKey,inputText);
for(int m=1;m<=9;m++)
{
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
cipherKey[i][j] = cipherKeySum[i][40-4*m+j];
}
}
ReShiftRows(inputText);
ReSBoxFunc(inputText,reInputTextEncrypt);
RoundKeyXOR(reInputTextEncrypt,cipherKey,reInputTextRoundKeyXOR);
ReColumnMix(reInputTextRoundKeyXOR,inputText);
}
for(int i=0;i<4;i++)
{
for(int j=0;j<4;j++)
{
cipherKey[i][j] = cipherKeySum[i][j];
}
}
ReSBoxFunc(inputText,reInputTextEncrypt);
ReShiftRows(reInputTextEncrypt);
RoundKeyXOR(reInputTextEncrypt,cipherKey,inputText);
}
int main()
{
unsigned char inputText1[4][4]={{0x42,0x6c,0x20,0x74},
{0x6f,0x6f,0x61,0x68},
{0x62,0x6f,0x74,0x69},
{0x20,0x6b,0x20,0x73}};
unsigned char inputText2[4][4]={{0x1e,0xca,0xd6,0xce},
{0x03,0xf8,0x98,0xfa},
{0x40,0x7e,0x93,0x4d},
{0xd2,0xc8,0x82,0xd1}};
unsigned char cipherKey[4][4] = {
{0x3c,0x57,0x90,0xac},
{0xa1,0xf0,0x2c,0xc1},
{0x0b,0x19,0x13,0x07},
{0x21,0x16,0x80,0xbd}
};
unsigned char cipherKeySum[4][44] = {0};
CipherKeyExtended(cipherKey,cipherKeySum);
printf("***********AES加密解密运算***********\n要进行加密的明文为:\n");
printMatrix(inputText1);
printf("\n要解密的密文为:\n");
printMatrix(inputText2);
printf("\n密钥扩展为:\n");
for(int i=0;i<4;i++)
{
for(int j=0;j<44;j++)
{
printf("%.2x ",cipherKeySum[i][j]);
}
printf("\n");
}
printf("\n===============================================================================================\n\n");
Encrypt(inputText1,cipherKeySum);
Decrypt(inputText2,cipherKeySum);
printf("加密后的结果为:\n");
printMatrix(inputText1);
printf("\n解密后的结果为:\n");
printMatrix(inputText2);
return 0;
}
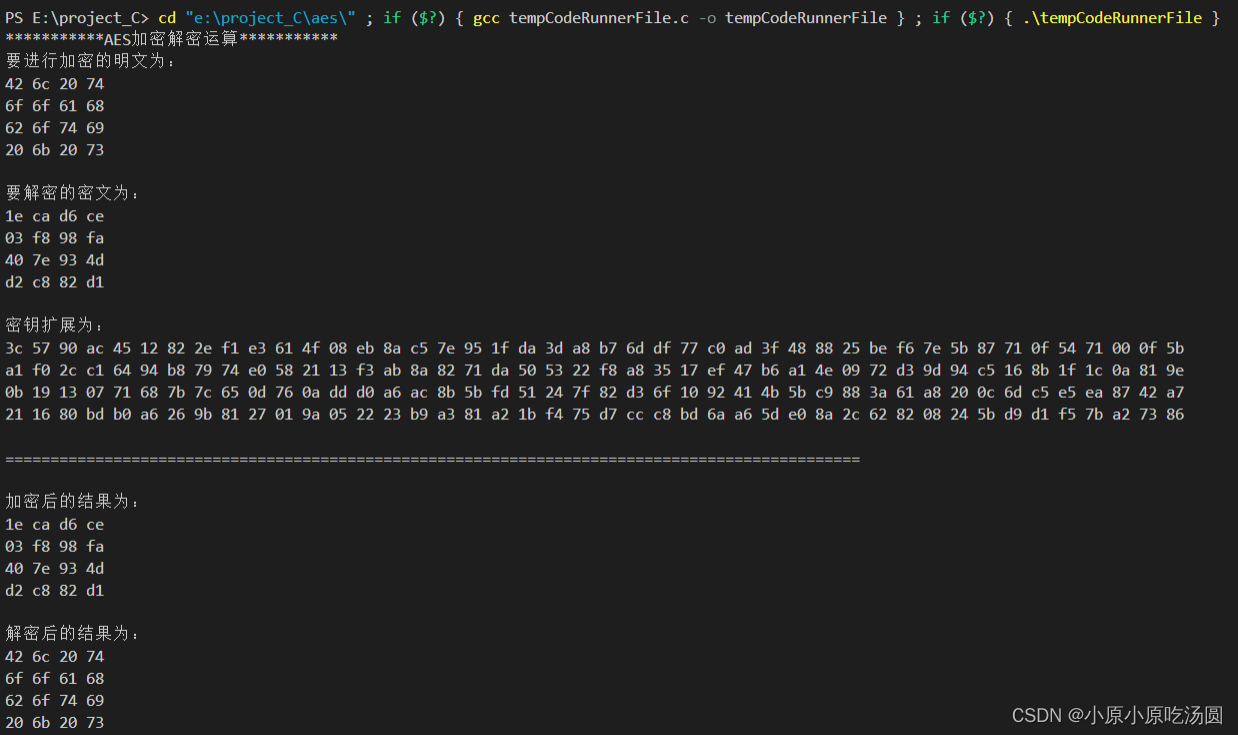
运行结果如下所示:
欢迎大家评论和收藏!!!