Algo_网络流概念,最大流初步认识

catalog

性质
-----------------------------------
Base
网络流算法-TIPS
- version——————
英语字符
流网络
最大流-FF方法
- EK算法
- - 示例
  - 性质
  - 时间
  - 劣势、改进
- Dinic

性质

残留网络的可叠加性

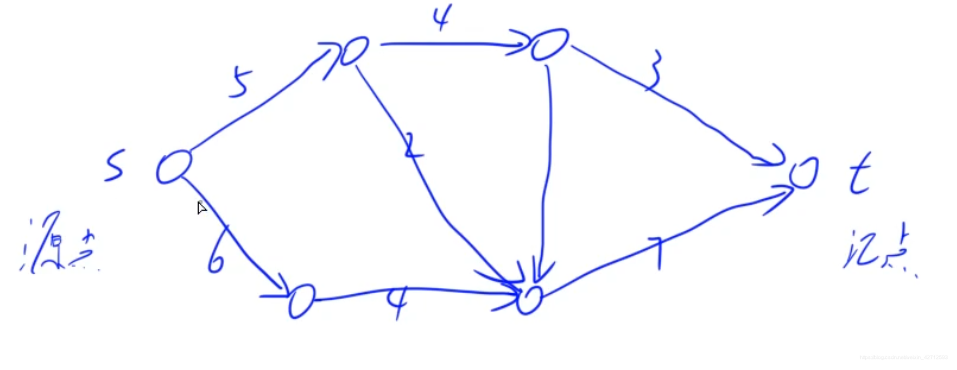
比如说: 你在二分 [0, 1, 2, ...., n], 每一个数都对应一个图, 如果用二分, 则比较耗时 因为每次二分, 都是在建立一个全新图!!! 这很耗时
但如果说, [0, 1, 2, 3, ..., n] 对应的图, 是动态增长的 即: (i)点的图是在(i-1)图的基础上, 新加入一些点和边
此时,

ji we给定你一个 "动态增长"的图, 则这个图存在叠加性 (每次的叠加, 都是在原图的基础上, 新加入一些点和边)d

即, 图Pre -> (加上一些新的点和边 {也可以说是一个图}) -> 图Cur

对应的, 图Pre的残留网络restPre -> (加上一些新的点和边 (称为: restAdd}) -> 图Cur的残留网络restCur

假如说, 我们现在已经知道了: 图Pre 的最大流, 如何去求图Cur 的最大流呢??
(所谓的: 知道图Pre的最大流, 意味着: 我们现在有一个 restPre_ans的残留网络. 注意, restPre_ans 是 restPre 跑过dinic后的状态; 他俩是不一样的)

当然最直接的办法是: 根据图Cur 构造出 restCur残留网络.
即: delete掉restPre_ans这个图, 然后再new 一个新的 restCur, 这自然很耗时.
(因为restCur != restPre_ans + restAdd, 所以已有的restPre_ans用不上, 只能delete掉)
也就是, 这种办法: 完全是把Pre图和 Cur图, 当成是2个图, 完全没有任何关系

其实, 比如, Pre图的最大流是: pre_ans
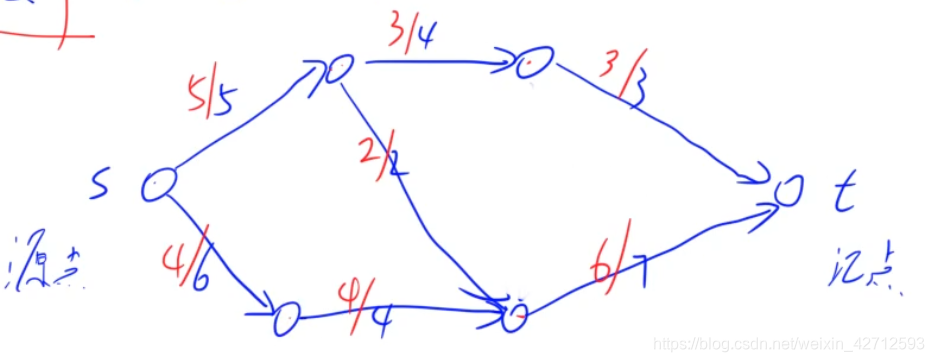
对于已得到的restPre_ans 残留网络(此时他的最大流肯定是0, 因为已经榨干了), 直接加上 restAdd后, 得到restNew残留网络
然后对restNew求最大流new_flow
则, pre_ans + new_flow 就是Cur图的最大流.

证明 即, 为什么: (restPre)的最大流 + (restPre_ans + restAdd)的最大流 = restCur的最大流:
对于(restPre_ans + restAdd)这个残留网络, 我们让其中的: restPre_ans(已榨干) 将他恢复成原状: restPre
此时有: (restPre + restAdd), 而他就等于: restCur

算法为:

Graph rest; ' rest为: 残留网络, 他是一个动态的过程 '

int maxFlow = rest.dinic();

FOR(;;){
   	' 模拟 每次从Pre -> Cur的过程 '
	
	rest += restAdd;  ' 将新加边 添加到 rest里 '

	maxFlow += rest.dinic();	' 这里是重点!!! '

	' 此时的maxFlow, 就是Cur图的 最大流 ' 
}

注意, 虽然restAdd里 (有点, 也有边), 但在实际算法里, 只会新加 "边", 即: rest += rsetAdd这个操作, 其实就是对rest进行了addEdge操作
因为在算法上, 新增加点 这太耗时了push_back; 即, 在最开始的rest这个图, 你应该把点数全部都提前弄出来

流网络的点和边

流网络里: 点: 是不能存储流量的(除了源汇点), 点也没有容量的概念, 我们知道wth[i], 而其中的i 是边, 不是点.

(当然, 其实边也不能存储流量…)

边和点, 都不能存储流量

但是: 边, 有"容量和流量"的概念, 即: 这个边, {流量: 流过了多少流量} {容量: 还能流多少流量}, 这是要记录下来的

(当然, 点也可以有"流量", 即一个点经过了多少流量 但这也是通过计算边来计算点的流量, 但是, 点没有 容量 这个性质)

虽然, 点不能存储流量, 但是, 点是要: 转移流量/ 流过流量的!!!
可以想象成: 一些入边流给了: 一个点, 很多流量, 而这个点需要将这些流量通过出边, 全部的流出去

即, 虽然每个点, 都是流量守恒, 即( 存储流量为0), 但是, 点也是有流量这个概念; 点的流量为: 可行流中, 该点 "流过"了的流量

最小割定理证明

在这里插入图片描述

-----------------------------------

Base

所谓“流”，其实就是一个：带权有向图

其实这里讲的朴素意义下的最大流，他完整的名称是：

有源汇：即这个流(有向图)，他有唯一的一个起点beg，有唯一的一个终点ed
下界为0：即原G的边wth为k，则该边流量是[0, k]范围。也就意味着：该边的下界为0，上界为k
因为下界为0，所以通常称为：无上下界
等流： beg流出多少 = ed流入多少。因为所有其他点都不存储流量。

网络流算法-TIPS

add_edge建边函数，一定要成对的调用！！！
因为wth对应残留网络，残留网络所有边，都是成对的！！（这是规定！！）
add_edge(a, b, w), add_edge(b, a, 0);
即使某一个边是无用的，也是成对创建出来！！！

比如， x->源点beg，其实残留网络中根本不需要x->beg这条边，因为任何一个流量，不可能再流回到beg里去！！
再比如，也不需要ed->x的边，因为任何一个流量，不可能从汇点ed在流出去！
但是，你还是要把x->beg, ed->x这些边给创建出来！!

因为，我们的dfs函数里 wth[i] -= k, wth[i^1] += k如果你没有成对建边，那么wth[i^1]就会影响其他正常边
总之，就记住，一定要：成对的调用add_edge
关于wth[]边权
wth[]这个数组非常非常重要，以往图论中这个数组往往是静态不变的，而在网络流中他是一直在变的！！
因为，我们维护的图，是残留网络，准确说是：当前最大流，的，残留网络
而，当前最大流，他是在不断扩大，导致其对应的残留网络不断的变化。
最终的wth：即残留网络的容量，他表示的是：每条边，还可以流多少流量

思考一个问题：如果我们想要得到，最大流这个图
有一个思路是：我们提前memcpy(init_wth, wth) ，最终遍历所有的(正向，即偶数号)边i，那么，init_wth[i] - wth[i]，便是最大流的值

当然，你可能会疑问，残留网络可以退流，即在反向边（奇数号经过流量，即，这个边，会出现在最大流中
为什么只用考虑正向边呢？明明反向边是有流量的！！
因为，所有的正向边(偶数号)，他就是原生图G的边！！！我们所构建的图，他是残留网络，反向边是我们自己补充的
即，用户/问题，他只知道的是原生图G的边，根本就没有反向边这个概念，这个我们自己填充进去的。
再来解释下这个现象，为什么反向边有流量，而最大流无需考虑这个边
a->b是正向边，wth[a,b]=4, wth[b,a]=3
说明，a->往b，流了3的流量（因为反向边的容量是3），即反向边的值，其实完全是从正向边推导来的！！
反向边的wth = 正向边的init_wth - 正向边的wth
反向边[b,a]，只是算法所需，根本不说明： b往->a流的流量！！

注意，残留网络的边权，即wth，表示：这条边还能流多少流量（并不表示，最大流的流量）
但，最大流的流量，可以通过残留网络推理出。
从wth[a,b]=4, wth[b,a]=3，你只能得到一个信息：在真实的最大流中，a->往b，流了3的流量！！！
也就是， a->往b，流了3的流量，他对应到残留网络中，对应了，2条边权>0的边！！

你要得到，最大流中，a->b的流量，有2种方式：
比如，i是a->b在残留网络的边(i肯定是偶数)
则，(wth[i ^ 1]) = (init_wth[i] - wth[i]) = 最大流中a->b的流量
所以，也无需init_wth数组，wth[i^1]便是最大流流量（前提是i是偶数）
当然，这只是通过i得到的，a->b的流量。实际a->b的流量要更大，因为a->b的边有很多
而且，一旦有(wth[i^1] != 0)，即a->b有流量，那么必然没有b->a的流量
dfs算法中，为什么要加入if( wth[i] == 0 ){ continue; }的判断？
按说我们刚建立完分层图，只要符合是分层图，这条边就是!=0的，为什么要重复判断呢？
1. 比如(a -> b)，有很多的边{q,w,e,r}，建立分层图时，可能是依据r这个边（即wth[r]!=0, wth[q,w,e]=0）
  而我们for循环，是从q开始的！！！
2. 比如(a->b)，虽然depth[b] = depth[a] + 1 ，但是b点并不是根据a点建立的！！！
  即, (a->b)的所有边都是0。只不过有一个点c，depth[c] = depth[a]
  depth[b]的值，是根据c点确立的！！！
dfs算法中，每次for循环，更新first_edge[cur] = i;，不要写成nex[i]，因为当前边可能不会用完，即pre_f很小

version——————

英语字符

c： capacity 容量
f： flow 流量

流网络

流网络，是一个 有向图，有1个源点beg，1个汇点end

边：
	每条有向边，有一个权重，表示为： 该水管的速率的最大值 （也就是： 限制）

源点：
	可以想象成是：一个无穷大的水库，无穷多的水 可以流出去
	即， 将水 通过各个管道，源源不断的 流入 汇点

汇点：
	可以想象成是：大海， 可以接收无穷大的水 流入

流网络这个图，G = (v, e)   ' 表示： 由点和边 组成 '

在这里插入图片描述

反向边

	我们可以假定，两点之间 最多只有1条有向边 a -> b
	不会出现： a->b  和 b->a， 同时存在的情况。
	这样便于我们处理。

但是，注意，如果(a->b) 和 (b->a)都存在，你不可以做“抵消操作”！！
 比如： (a->b)=10， (b->a)=5
     你不能把这2条边，变成是：  (a->b) = 5 ！！
     这是完全不正确的！！！
  因为，原来(a->b)最大可以流10，你现在最大只能流5
'就比如，一个人：好心有100，坏心有50。 你不能说，他只有好心50，没有坏心！！'
  原来以a->b为正方向，通流量为[-5, 10]； 而你现在只有[0, 5]

这样处理 是完全错误的！！
我们可以做一个， 特殊的处理：  
		当存在：   a->b    和   b->a 时，
		令a->b，中间添加一个c点，变成：
		 a -> c -> b 和 b -> a，  此时，就没有反向边了

' 因此，对于网络流：  两点之间 最多只有1条 单向边 '

在这里插入图片描述

可行流

可行流，一般用f表示，他需要经过原G的 所有点！！！
	我们自己去指定， 每条边的权重（即每个水管的速率）
 需同时满足：
 	1， 容量限制	（比如，一条边的权重是5，那么 你自定义权重时 <=5，不能超过）
 		0 <= f(a, b) <= wth(a, b)   ' 可行流中ab权重 <= 原本ab边权 '
 	2， 流量守恒 （除了 源点和汇点，其他的所有点 都是不存储水的！！！）
		即，其他的点：  流入多少水，就必须流出多少水 
		' 入度边的权重之和 == 出度边的权重之和 '
		因为所有点都不存储水，因此：  每秒， 源点流出去的水 == 汇点流入的水


' 一个网络流，会有很多的 可行流！！！ '

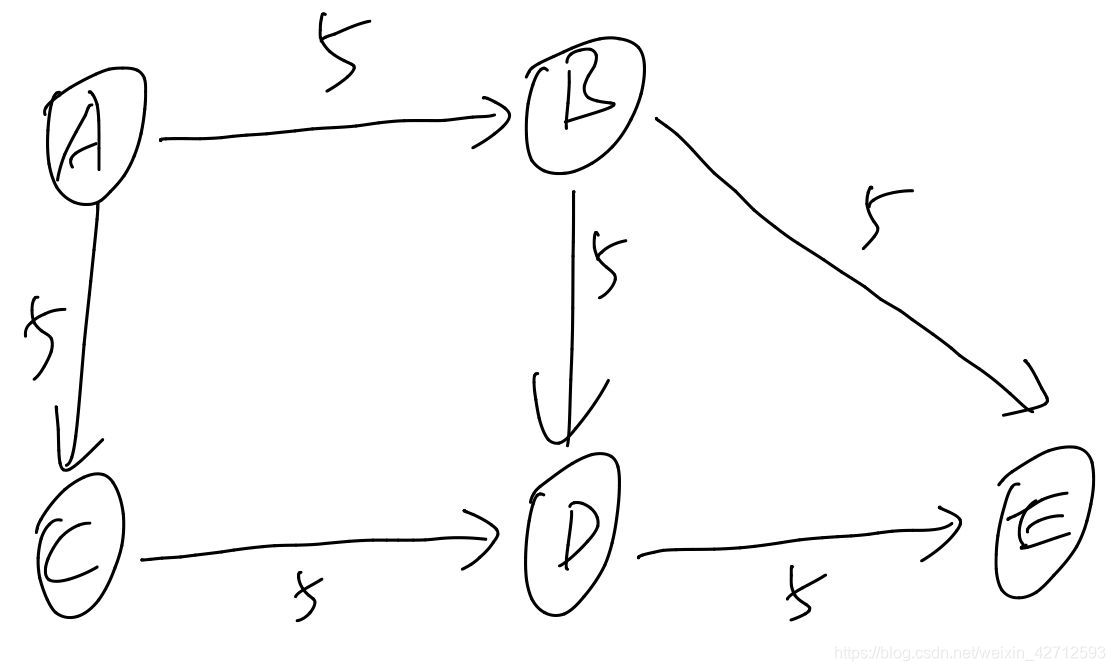
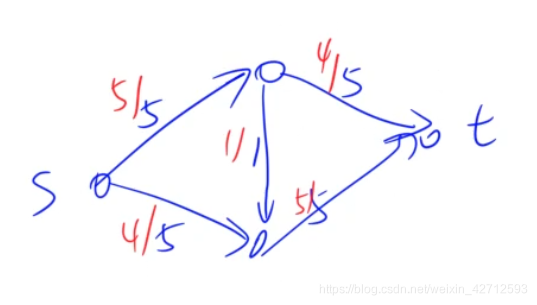
红色的边权，是我们指定的，所有红色的边权，构成一个可行流。
在这里插入图片描述

流量值

可行流的流量|f| = 每秒源点流出的水 = 每秒汇点流入的水
	我们以： 每秒源点流出的水，定义为 一个可行流的流量
	|f| =  源点流出的水 - 源点流入的水
	 ' 一般情况，不存在流入源点的情况。 但特殊情况会有 '

最大流

对于一个流网络来说，他会有很多的 可行流，每一个可行流 都可以求一个流量值
最大流：  流量值最大的一个 可行流

空可行流

在求解“最大流”的算法中，ans最初就是从“空 可行流”开始
然后，不断的找 增广路径，将增广路径 加入到ans这个可行流中，使ans变大
  所以，定义这个 “空 可行流”，是非常有必要的

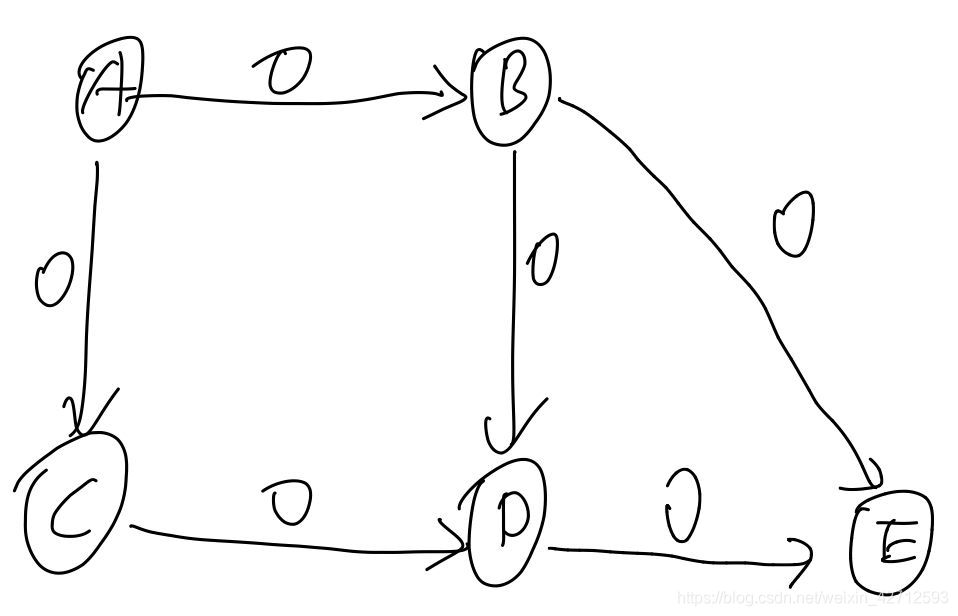
原流网络G 的 空可行流f：
	1，G有n个点，则f也有这n个点
	2，G有m个边，则f也有这m个边（且f的这个m个边，边权均为0）
' 注意： G中，任意两点 最多有1条单向边！ 且边权>0 （这个流网络G的前提）'

原流网络G
在这里插入图片描述
他的空可行流：（原BC间没有边，则空可行流BC也没有边）

可行流的性质

原流网络G 的 任一可行流f：
	1，G有n个点，则f也有这n个点
	2，G有m个边，则f也有这m个边（且f(a, b) <= G(a, b)）
	3, 因为原G有(a,b)边，所以，f也有(a,b)边
		而且，原G一定没有(b,a)边！！！ 所以，f也没有(b,a)边

比如，可行流f 的边(a,b) == 3  （原G的(a,b) = 5）
f的残留网络中，有个增广路径： 是边(b,a) = 3 {
   一定是<=3的，因为残留网络(b,a)=3, (a,b)=2}
  ' 增广路径和可行流的(a b)两点，肯定是单向边，但方向未知 '
  我们知道，这个增广路径，是要加入到 这个可行流f 中去的
  ' 增广路径有(b,a)边，这违背了： 可行流 不能有(b,a)边 这个规定！！ '
  '  因为，原G 只有(a,b)边，意味着： 可行流 也必须有(a,b)边，不能有(b,a)边 '
  
所以， 此时就要做： “抵消操作”！！！
因为， 增广路径(b, a) <= 可行流(a, b)   ' 这是个性质！！ '
所以， 不要把(b, a)加入到可行流中（这就违背规定了）
  你直接让：  可行流(a, b) -= 增广路径(b, a) 即可！！！

' 关于抵消操作：   '
	' 对于“水管的容量”（流网络，残留网络），不能做“抵消操作”！！ '
	' 容量是一种“限定” '
	' 而对于“实际的流水量”（可行流、增广路径），可以做“抵消操作”！！'
	' 因为，实际的流水量： 你流出5 再流入5，相当于 0 '

残留网络

残留网络，是针对 某一个可行流 来说的； 
不同的可行流，残留网络也不同
	即，残留网路 是和 可行流，一一对应的。

一个网络流： $G$
某一个可行流： $f_{1}$
f1这个可行流，对应的残留网络： $G_{f_{1}}$

可行流f1为：（下图的红色）
在这里插入图片描述
则该f1可行流，对应的残留网络 $G_{f_{1}}$ ，需满足：

  1，  如果可行流中，存在a->b的边 （肯定有： f(a, b) <= wth(a,b) ）
  		' f(a, b)为可行流， wth为最初的流网络 即最大容量 '
  	 则在残留网络中， G_f(a, b) = wth(a,b) - f(a,b)
  	 	表示，其还剩余的 上升空间（a->b： 网络流是5，可行流是3，则残留网络为2）
  2，  如果可行流，不存在a->b的边
  	 则添加“反向边b->a”， G_f(b, a) == f(a, b) 反向边权==正向可行流

则该可行流f1，所对应的残留网络为：
f1中的正向边： wth变为剩余容量；（该边肯定没有反向边 {这个可行流所规定的}）
则现在，添加该边对应的反向边，wth为 f1中该边的容量。
在这里插入图片描述

添加反向边

只有在“残余网络”里，才有会“反向边”的概念（在网络流和可行流，都没有！）

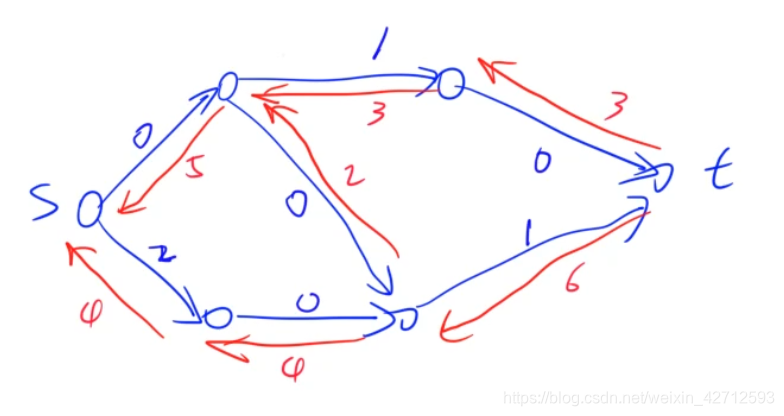
下面的红色，是该流网络的最大流，流量为9
在这里插入图片描述
但是，如果我们可以考虑 “反向边”。比如中间的那个 wth=1的边
a->b： wth(a, b) = 1
考虑反向边，意味着：我们可以从b 反向往 a，退回去1的流量
即，可以退回去的流量大小。

注意，上图的最大流是9（他已经达到平衡！！！）
你新加流以达到更大的流量，前提是不得打破原来的平衡
因为原来是平衡，你现在增大流量后，也得是平衡的即：可行流

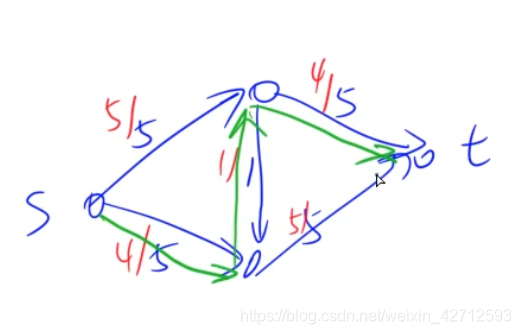
在这里插入图片描述
上面的3条绿色，权重都是1
其中，第1条和第3条，都是在原先正向边的基础上增大由4变成5
重点是：第2条绿色，他是“反向边”！！即退回去1个流量
主要，你新加的这3条边后，必须保证：仍然是可行流
即，每个点流入和流出是相同的。
其实，你可以看成是，中间的那2个点：原先有流量为1，现在没有流量了为0

抵消操作

抵消操作：  让(a->b)=x, (b->a)=y  “变成：”  (a->b) = x-y
   ' 即，让2条边 变成 1条边 '

在残留网络中，点(a, b) 是会有2条边的！！  a->b 和 b->a
  比如，可行流f1(a->b)=2， G(a->b)=6
  则残留网络R_f1(a->b)=4, R_f1(b->a)=2
  即对于R_f1残留网络： 有(a->b)=4, (b->a)=2
  ' 此时，你不可以做抵消操作！！！！ '
  ' 如果此时做抵消，则变成： (a->b)=2， 这是不正确的！！！ '
  残留网络有： (a->b)=4, (b->a)=2
  意味着：  该残留网络的任意可行流f
  	    f(a->b)=[0,4]  && f(b->a)=[0