1.线性回归问题

什么是线性回归？简单举个例子，给定一个直线方程 $y=kx+b$ 和位于该直线上的两点$(x_1,y_1)$、$(x_2,y_2)$。问$x=x_3$时，$y=y_3=?$ 根据中学知识，先利用已知两点求解直线方程参数$k$、$b$，再利用求得的直线方程求$y_3$值。该求解过程就是一个简单的线性回归问题。
我们的现实生活中，有很多问题都可以看作是线性回归问题，如：预测房屋价格、气温、销售额等连续值问题。在深度学习中，一般会提供大量的数据，用于估计线性模型，最后根据模型完成回归任务。

2.线性回归模型

（1）模型定义

以房屋价格预测模型为例，我们假设房屋价格只取决于两个因素，即面积和房龄。设房屋的面积为$x_1$，房龄为$x_2$，售出价格为$y$。建立模型表达式为$$\hat{y}=x_1{w}_1+x_2{w}_2+b$$其中$w_1$和$w_2$是权重，$b$是偏置。$\hat{y}$表示对真实价格$y$的预测和估计。它们之间存在一定误差。
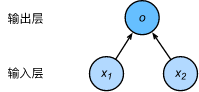
线性回归模型实际是一个单输出的单层神经网络。

（2）模型训练

①训练数据

通常我们需要收集包含有房屋真实售出价格以及它们对应的面积和房龄的数据集用于训练我们的模型。例如现在有房屋价格数据集$S$，其中包含的样本数为$n$，索引为$i$的样本的特征为$x_1^i$和$x_2^i$，标签为$y^i$表示的是房屋真实售出价格。对于索引为$i$的房屋，线性回归模型的房屋价格预测表达式为：$${\hat{y}}^i=x_1^i{w}_1+x_2^i{w}_2+b$$

②损失函数

房屋售出的真实价格与我们预测的价格之间存在一定的误差，这里我们使用平方误差去进行计算。评估索引为$i$的样本误差表达式为：$$l^i(w_1,w_2,b)=\frac{1}{2}({\hat{y}}^i-y^i{)}^2$$
在机器学习里，将衡量误差的函数称为损失函数。通常，使用训练数据集中所有样本误差的平均来衡量模型预测的质量，即：
$$l(w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n{l}^i(w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}(x_1^i{w}_1+x_2^i{w}_2+b-y^i)$$

③优化函数

在模型训练中，我们希望找出一组模型参数，记为$w_1^{\ast },w_2^{\ast },b^{\ast }$，使得训练样本平均损失最小。这就需要使用的优化函数，迭代更新模型参数，且每次更新都会使得损失函数的值减小。以下给出用最小梯度算法更新参数的表达式：
$$w_1\leftarrow w_1-\frac{\eta }{|\mathrm{B}|}\sum _{i\in |\mathrm{B}|}\frac{\delta l^i(w_1,w_2,b)}{\delta w_1}=w_1-\frac{\eta }{|\mathrm{B}|}\sum _{i\in |\mathrm{B}|}{x}_1^i(x_1^i{w}_1+x_2^i{w}_2+b-y^i)$$
$$w_2\leftarrow w_2-\frac{\eta }{|\mathrm{B}|}\sum _{i\in |\mathrm{B}|}\frac{\delta l^i(w_1,w_2,b)}{\delta w_2}=w_2-\frac{\eta }{|\mathrm{B}|}\sum _{i\in |\mathrm{B}|}{x}_2^i(x_1^i{w}_1+x_2^i{w}_2+b-y^i)$$
$$b\leftarrow b-\frac{\eta }{|\mathrm{B}|}\sum _{i\in |\mathrm{B}|}\frac{\delta l^i(w_1,w_2,b)}{\delta b}=b-\frac{\eta }{|\mathrm{B}|}\sum _{i\in |\mathrm{B}|}(x_1^i{w}_1+x_2^i{w}_2+b-y^i)$$
其中$\mathrm{B}$是由训练数据样本组成的小批量（min-bitch），$\eta$称为学习率。$\mathrm{B}$和$\eta$是人为设置，而不是通过模型训练所得，因此也称为超参数。所谓的“调参”，就是通过反复试错来找到超参数合适的值。

3.代码实现

Pytorch代码实现

import torch
import numpy as np
import random
import torch.utils.data as Data
from torch import nn
from torch.nn import init
from torch import optim

#生成数据集
num_inputs = 2
num_examples = 1000
true_w = [2,-3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0,1,(num_examples,num_inputs)),dtype=torch.float)#随机生成满足正态分布的样本特征
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b#计算真实标签
labels += torch.tensor(np.random.normal(0,0.01,labels.size()),dtype=torch.float)#加入随机噪声

#定义模型
class LinearRegression(nn.Module):
    def __init__(self, n_feature):
        super(LinearRegression,self).__init__()
        self.linear = nn.Linear(n_feature, 1)#线性回归相当于使用了一层全连接层
    def forward(self,x):#前向传播
        y = self.linear(x)
        return y
net = LinearRegression(num_inputs)

#初始化模型参数
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)

#定义损失函数
loss = nn.MSELoss()

#定义优化函数
optimizer = optim.SGD(net.parameters(), lr=0.03)

#读取数据
batch_size = 10#读取数据的批次大小
dataset = Data.TensorDataset(features,labels)#将训练数据的特征和标签组合
data_iter = Data.DataLoader(dataset,batch_size,shuffle=True)#随机读取小批量

#训练模型
num_epochs = 3
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        output = net(X)
        l = loss(output,y.view(-1,1))
        optimizer.zero_grad()#梯度清零
        l.backward()#反向传播
        optimizer.step()
    print('epoch: %d, loss: %f' % (epoch, l.item()))
    print(true_w, net.linear.weight)
    print(true_b, net.linear.bias)