1.分类问题

根据上一章，我们知道线性回归模型用于解决连续值预测问题。而解决离散值的预测，例如：图像分类等。就需要使用诸如softmax回归的分类模型。

2.softmax回归模型

（1）模型定义

现有分类问题，存在三种动物$y_i(i=1,2,3)$，每种动物有四个特征$x_j(j=1,2,3,4)$。对于每种动物都存在一个线性表达式为：
$$o_i=x_1{w}_{1i}+x_2{w}_{2i}+x_3{w}_{3i}+x_4{w}_{4i}+b_i$$
其中输出的最大值$o_i$对应的索引值$i$对应的类别$y_i$是我们预测的类别，为：${\hat{y}}_{argmax(o_i)}$
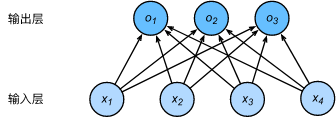
softmax回归模型实际是一个多输出的单层神经网络。

（2）softmax函数

在上述模型中，$o_i$的范围很难确定。并且由于真实的标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。所以使用softmax函数将输出值变换成值为正且和为1的概率分布：
$${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3=softmax(o_1,o_2,o_3)$$
$${\hat{y}}_1=\frac{exp(o_1)}{{\sum }_{i=1}^{3}exp(o_i)},{\hat{y}}_2=\frac{exp(o_2)}{{\sum }_{i=1}^{3}exp(o_i)},{\hat{y}}_3=\frac{exp(o_3)}{{\sum }_{i=1}^{3}exp(o_i)}$$
显然，${\hat{y}}_1+{\hat{y}}_2+{\hat{y}}_3=1$且$0\le {\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3\le 1。$

（3）交叉熵损失函数

为了计算损失，对于样本$i$，我们构造向量有${\mathbf{y}}^i\in {\mathbb{R}}^q$，使其第$y^i$个值为1，其余值为0。我们的训练目标可以设为使预测概率分布${\hat{\mathbf{y}}}^i$尽可能接近真实的标签概率分布${\mathbf{y}}^i$。
对于分类问题，我们常用的损失函数为交叉熵损失函数。由于平方损失函数过于严格，在分类问题中这是不必要的，我们只需要衡量两个概率分布差异即可。函数表达式如下：
$$l(\Theta )=\frac{1}{n}\sum _{i=1}^{n}H({\mathbf{y}}^i,{\hat{\mathbf{y}}}^i),H({\mathbf{y}}^i,{\hat{\mathbf{y}}}^i)=-\sum _{j=1}^q{y}_j^{i}log({\hat{y}}_j^i)$$

3.代码实现

Pytorch代码

import torch
import torchvision
from torch import nn
from torch.nn import init
from torch import optim

#网络模型
class SoftmaxRegress(nn.Module):
    def __init__(self,n_input,n_output):
        super(SoftmaxRegress, self).__init__()
        self.linear = nn.Linear(n_input,n_output)
    def forward(self,x):
        y = self.linear(x.view(x.shape[0],-1))#用view()将x的形状转换为(batch_size,28*28)再送入全连接层
        return y
 
#评价函数
def evaluate_accuracy(data_iter,net):
    acc_sum, n = 0.0,0
    for X,y in data_iter:
        acc_sum += (net(X).argmax(dim=1)==y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n

#获取MNIST数据集
minst_train = torchvision.datasets.FashionMNIST(root='D:/Datasets/FashionMNIST',train=True,download=True,transform=torchvision.transforms.ToTensor())
minst_test = torchvision.datasets.FashionMNIST(root='D:/Datasets/FashionMNIST',train=False,download=True,transform=torchvision.transforms.ToTensor())

#读取数据
batch_size = 256
train_iter = torch.utils.data.DataLoader(minst_train,batch_size=batch_size,shuffle=True,num_workers=0)
test_iter = torch.utils.data.DataLoader(minst_test,batch_size=batch_size,shuffle=False,num_workers=0)


#初始化模型参数
num_inputs = 28*28
num_outputs = 10
net = SoftmaxRegress(num_inputs, num_outputs)
init.normal_(net.linear.weight, mean=0,std=0.01)
init.constant_(net.linear.bias, val=0)

#定义损失函数
loss = nn.CrossEntropyLoss()#该函数包含了softmax运算和交叉损失计算

#定义优化算法
optimizer = optim.SGD(net.parameters(), lr=0.1)

#训练模型
num_epochs = 5
for epoch in range(num_epochs):
    train_l_sum, train_acc_sum, n =0.0, 0.0, 0
    for X,y in train_iter:
        y_hat = net(X)
        l = loss(y_hat,y).sum()
        optimizer.zero_grad()
        l.backward()
        optimizer.step()
        train_l_sum += l.item()
        train_acc_sum += (y_hat.argmax(dim=1)==y).sum().item()
        n += y.shape[0]
    test_acc = evaluate_accuracy(test_iter, net)
    print('epoch :%d,loss :%.4f,train acc :%.3f,test acc :%.3f'%(epoch+1,train_l_sum/n,train_acc_sum/n,test_acc))