1、定义

顾名思义，双指针即用两个不同速度或不同方向的指针对数组或对象进行访问，通过两个不同指针的碰撞从而达到特定的目的。

2、解决问题

在时间或空间条件有限的情况下使用单向遍历需要消耗大量的时间或者根本无法解决问题，这时候就需要我们使用双指针，通过指针的碰撞判断是否达到条件，从而解决问题。

双指针分为快慢指针和左右指针，左右指针通常在数组有序的情况下使用，快慢指针通常在单向遍历需要消耗大量时间，或者有特定要求限制的情况下使用。

首先介绍一下左右指针

左右指针通常在数组有序的情况下，从最小和最大端同时对数组进行处理，对满足特定条件的数组元素进行成对处理，快慢指针逐渐靠拢直至发生碰撞，则遍历完所有数组。

举个例子：

一个孤岛上有7个人重量54kg，55kg，56kg，57kg，58kg，59kg，70kg。她们需要逃生到安全的地方。现在有足够的救生艇，但是每个救生艇只能坐两个人，而且每个救生艇最大能承受113kg的重量，那她们最少需要多少救生艇才能全部逃生。

现在我们来分析，如果最重的人可以与最轻的人共用一艘船，那么就这样安排。否则，最重的人无法与任何人配对，那么他们将自己独自乘一艘船。这么做的原因是，如果最轻的人可以与任何人配对，那么他们也可以与最重的人配对。

那我们首先让她们按照体重排好队

那我们首先看最瘦的和最胖的，连个加起来有124斤，是坐不了一条船的

那我们只能让最胖的自己坐一条船，然后看第二胖的能不能和最瘦的一起坐船走，这时候用了一条船。

可以发现最瘦的果然和第二胖的人体重一共为113kg，她们是可以一起坐船走的，这时候一共占用了两条船，接下来继续看第二瘦和第三胖的人。。。。。。。

最后组队情况为：

54kg - 59kg，55kg - 58kg，56kg - 57kg，70kg

从上我们可以看到双指针即是在有序数组的情况下，我们通过两个指针在遍历的过程中进行标记，对满足条件的进行处理，直至遍历完整个数组。

下面看几个例题：

881. 救生艇

第 i 个人的体重为 people[i]，每艘船可以承载的最大重量为 limit。

每艘船最多可同时载两人，但条件是这些人的重量之和最多为 limit。

返回载到每一个人所需的最小船数。(保证每个人都能被船载)。

示例 1：

输入：[2,1,4,7,3,2,5]
输出：5
解释：最长的 “山脉” 是 [1,4,7,3,2]，长度为 5。
示例 2：

输入：[2,2,2]
输出：0
解释：不含 “山脉”。
 
提示：
0 <= A.length <= 10000
0 <= A[i] <= 10000

如上所述：如果最重的人可以与最轻的人共用一艘船，那么就这样安排。否则，最重的人无法与任何人配对，那么他们将自己独自乘一艘船。

这么做的原因是，如果最轻的人可以与任何人配对，那么他们也可以与最重的人配对。

代码如下：

class Solution {
    public int numRescueBoats(int[] people, int limit) {
        Arrays.sort(people);
        int i = 0, j = people.length - 1;
        int ans = 0;

        while (i <= j) {
            ans++;
            if (people[i] + people[j] <= limit)
                i++;
            j--;
        }

        return ans;
    }
}

快慢指针

快慢指针中的快慢即两个指针移动的快慢不同，通过两个指针移动速度的不同，判断数组或链表的长度、是否有环、特定位置的数值等。

举个例子：

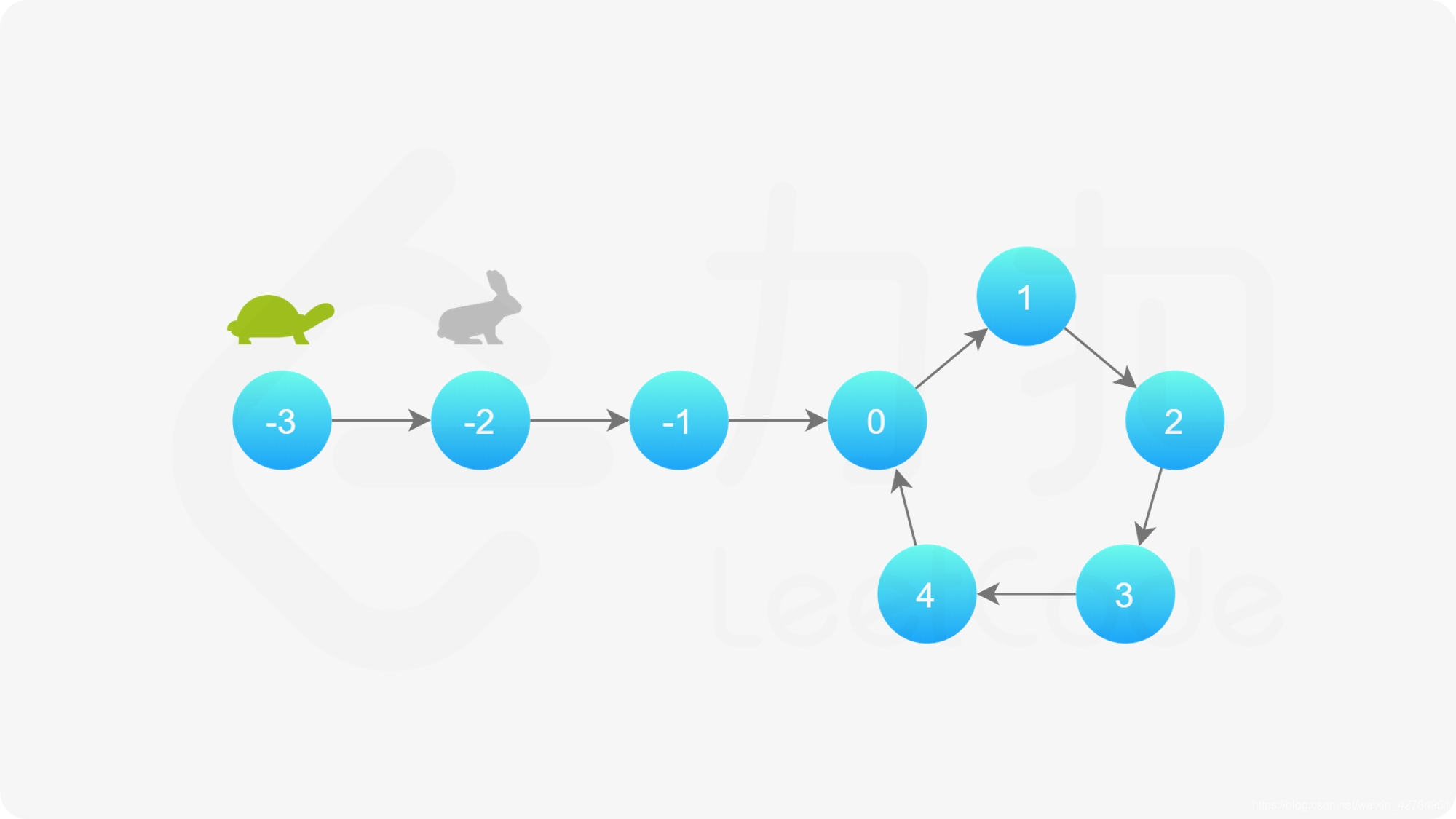
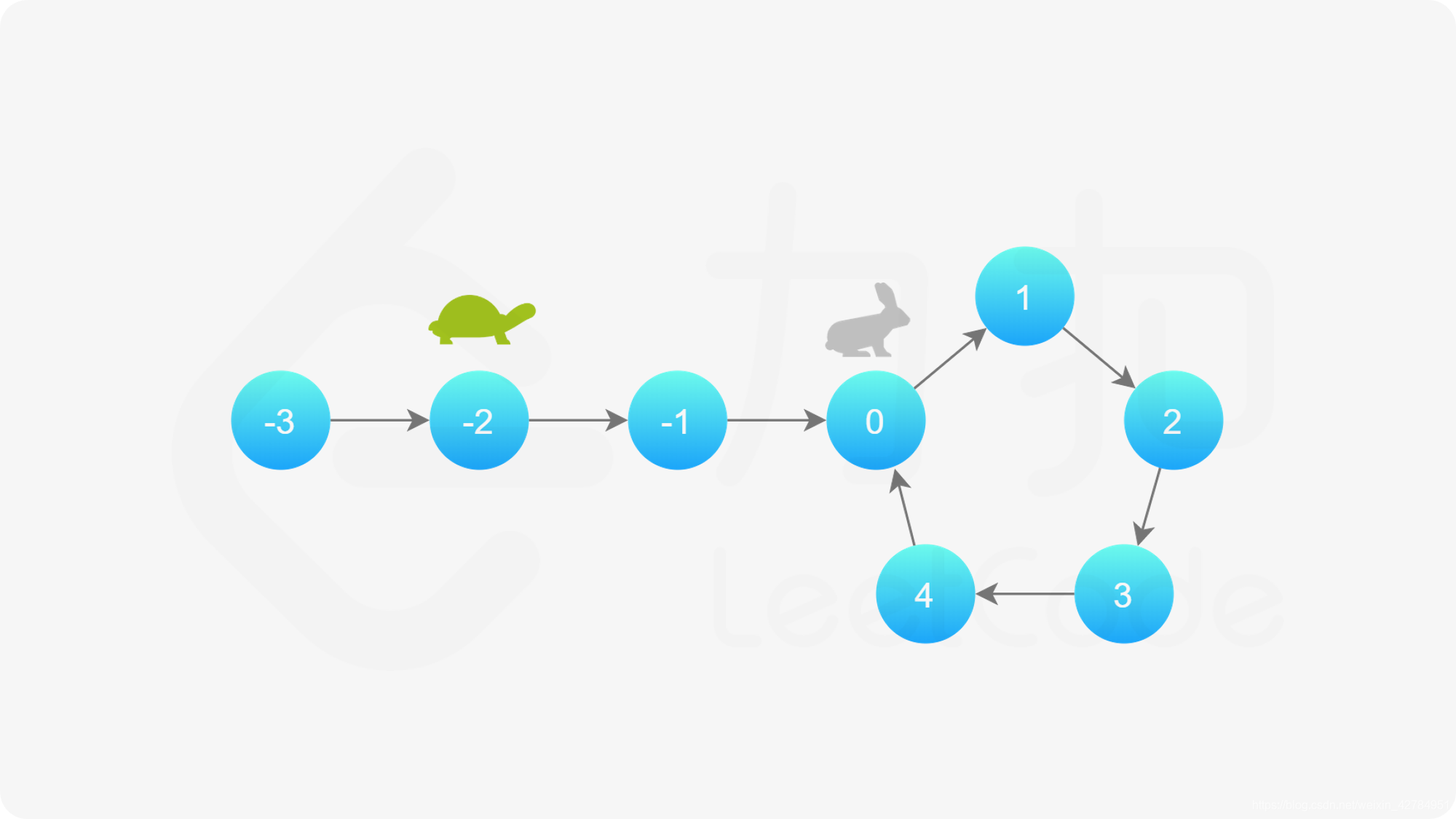
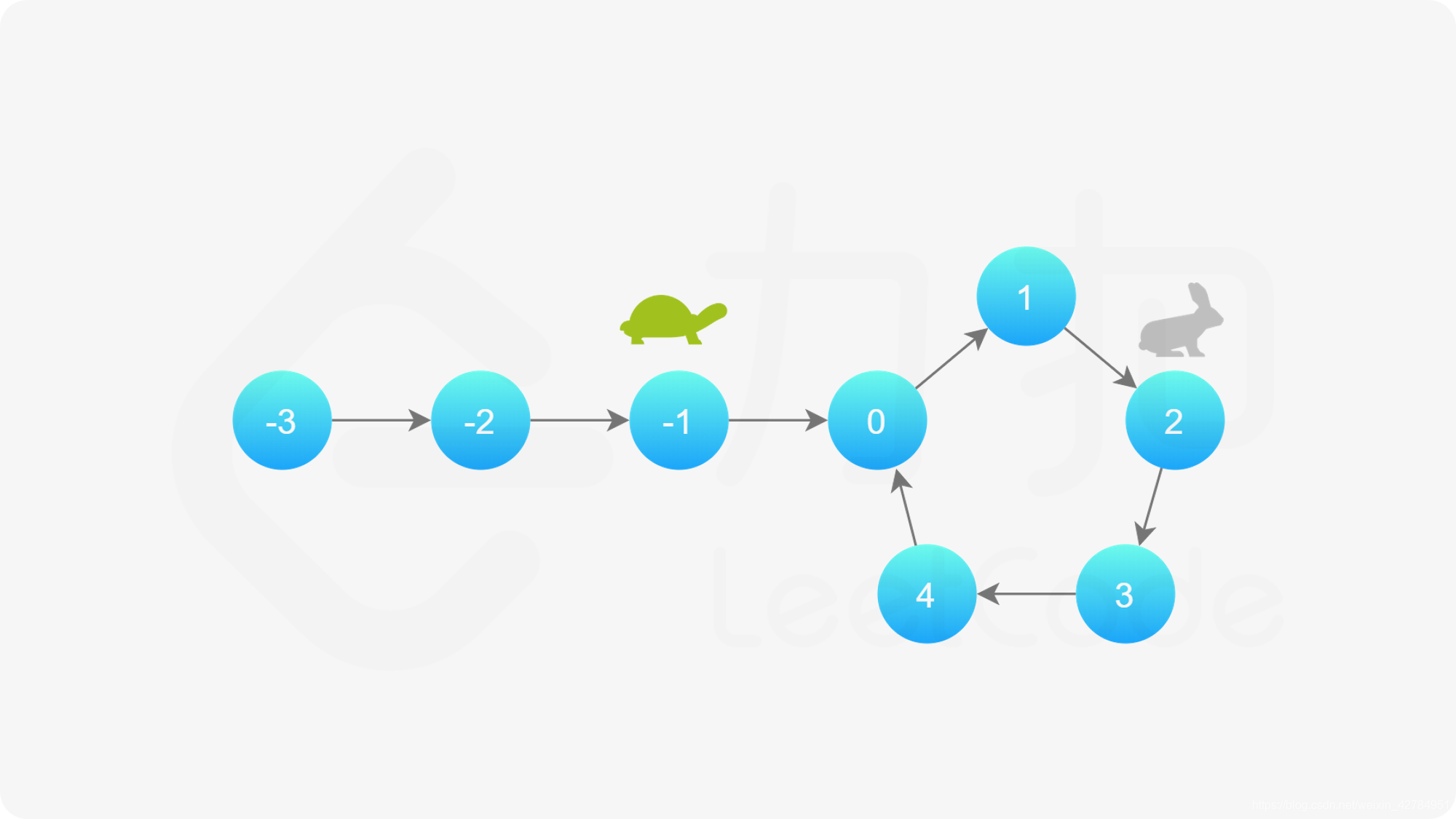
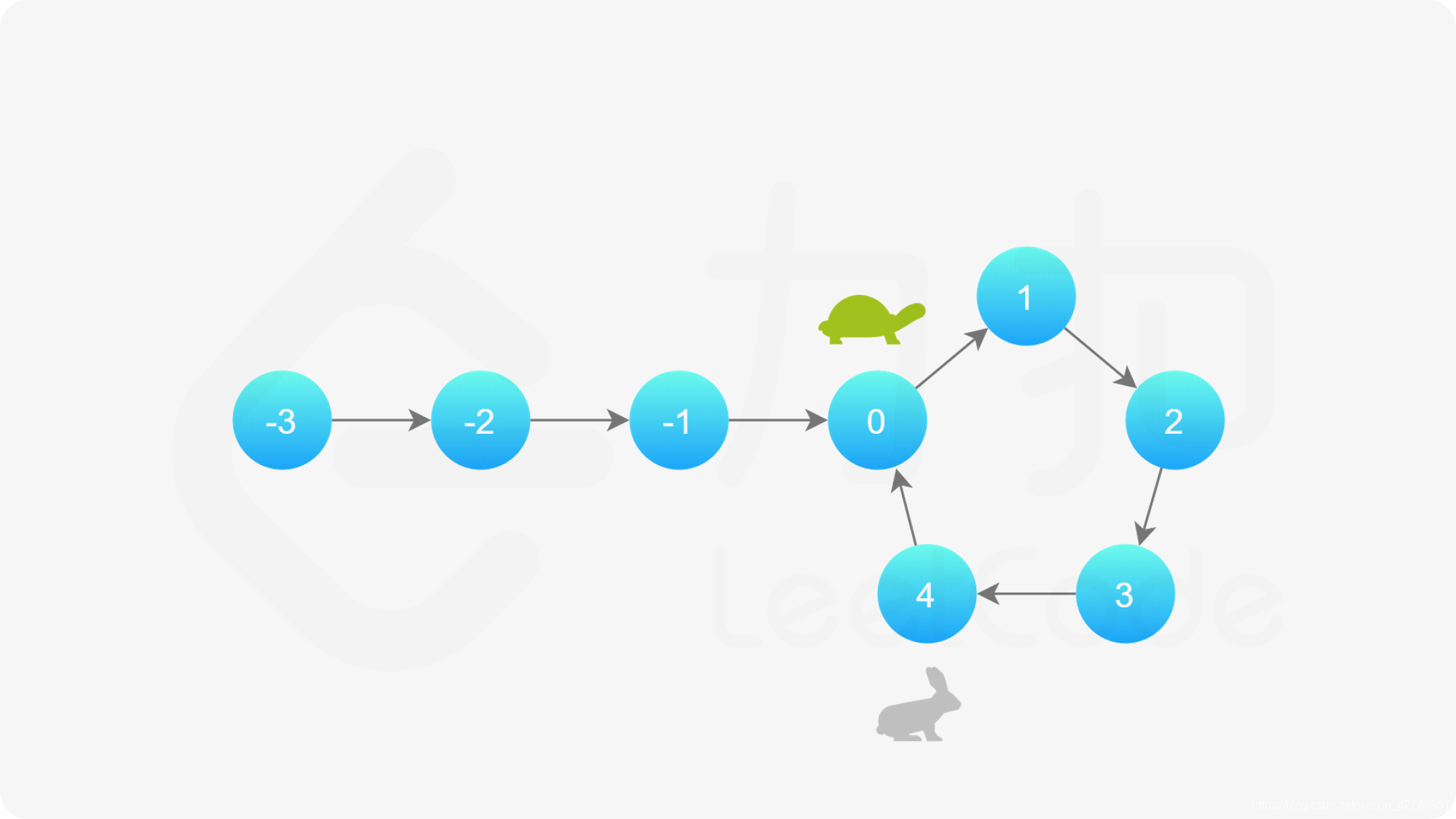
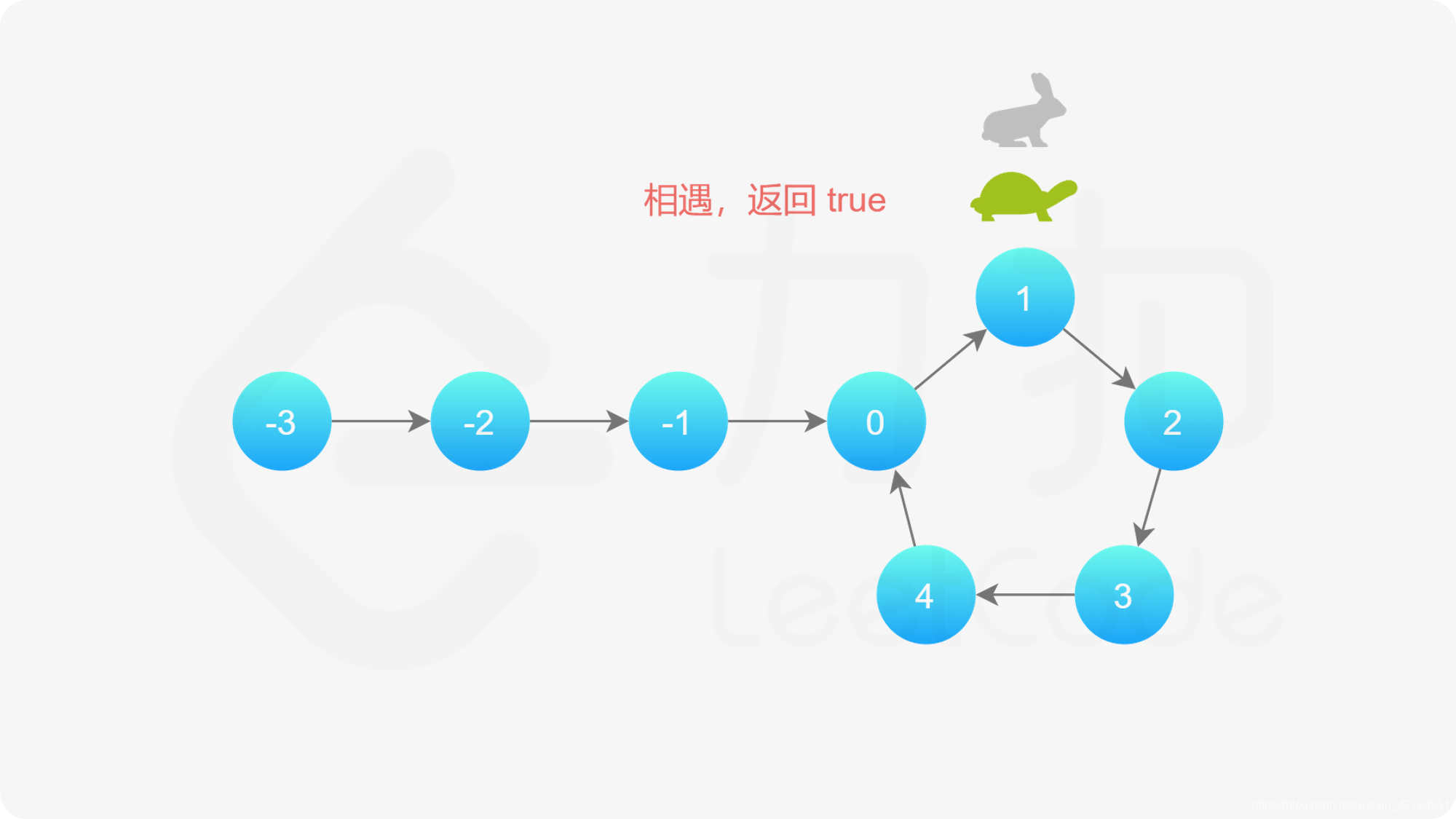
假如有一条跑道，假如有环，会沿着环一直跑，乌龟每次走一步，兔子每次走两步，那么如果有环，那么他们必定会相遇，过程如下：

环形链表问题：

141. 环形链表
142. 环形链表 II

回文链表问题：

对于回文链表问题，使用快慢指针解决，快指针步长为2，慢指针步长为1，则当快指针移动到链表末尾的时候，满指针正好移动到链表的中点。我们可以将链表的后半部分反转（修改链表结构），然后将前半部分和后半部分进行比较。

如下题：

234. 回文链表

回文链表问题可以分为5个步骤：

1. 找到前半部分链表的尾节点。
2. 反转后半部分链表。
3. 判断是否回文。
4. 恢复链表。
5. 返回结果。

class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null) {
            return true;
        }

        // 找到前半部分链表的尾节点并反转后半部分链表
        ListNode firstHalfEnd = endOfFirstHalf(head);
        ListNode secondHalfStart = reverseList(firstHalfEnd.next);

        // 判断是否回文
        ListNode p1 = head;
        ListNode p2 = secondHalfStart;
        boolean result = true;
        while (result && p2 != null) {
            if (p1.val != p2.val) {
                result = false;
            }
            p1 = p1.next;
            p2 = p2.next;
        }        

        // 还原链表并返回结果
        firstHalfEnd.next = reverseList(secondHalfStart);
        return result;
    }

    private ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode nextTemp = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nextTemp;
        }
        return prev;
    }

    private ListNode endOfFirstHalf(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        return slow;
    }
}

链表中倒数第K个节点问题

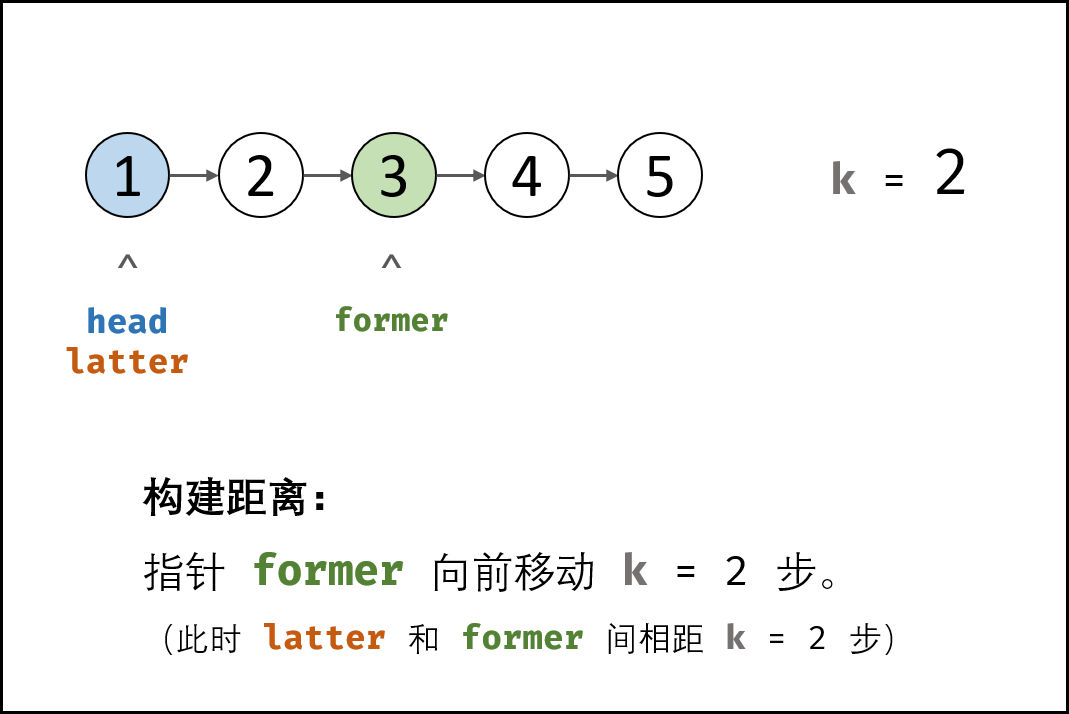
1. 初始化： 前指针 former 、后指针 latter ，双指针都指向头节点 head​ 。
2. 构建双指针距离： 前指针 former 先向前走 kk 步（结束后，双指针 former 和 latter 间相距 kk 步）。
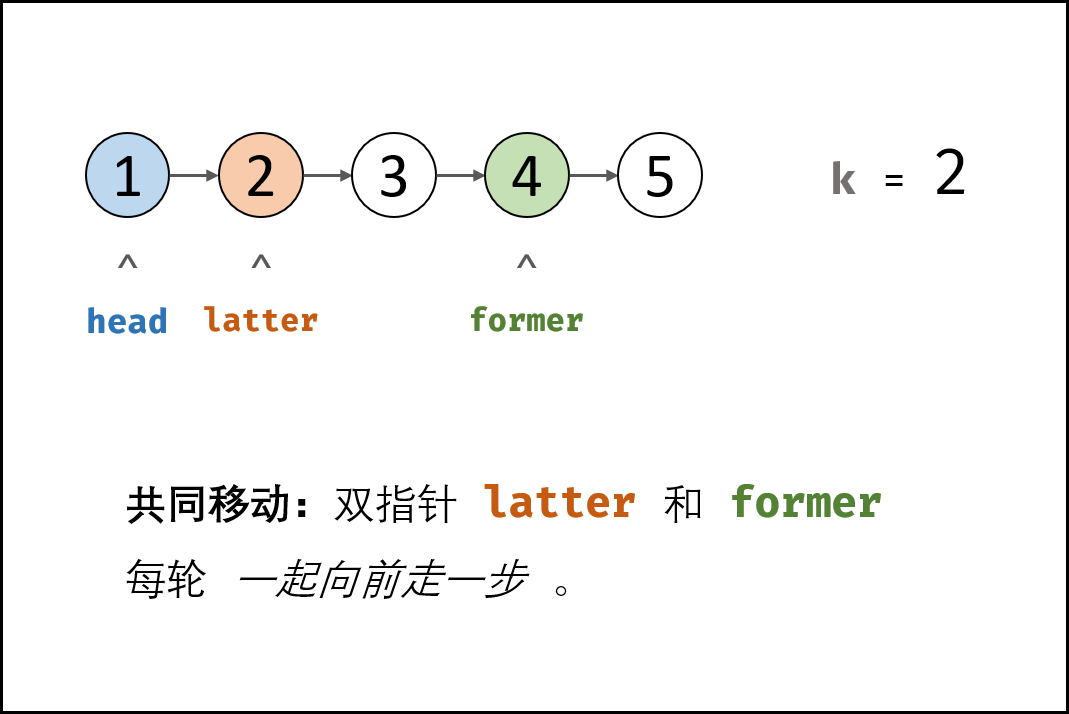
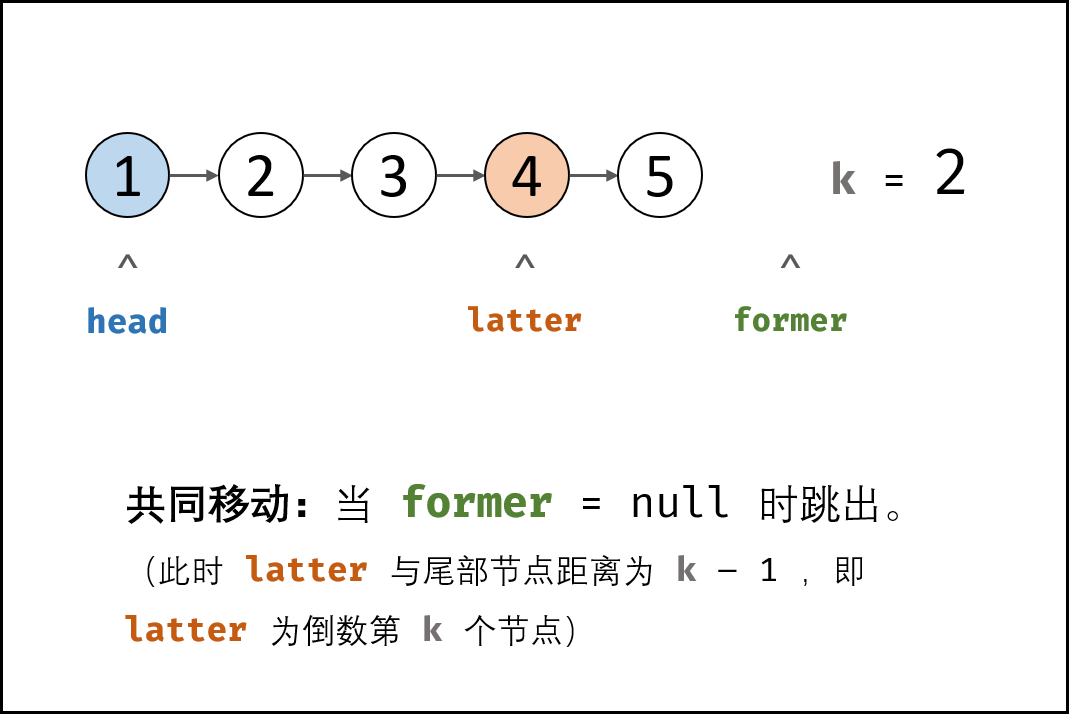
3. 双指针共同移动： 循环中，双指针 former 和 latter 每轮都向前走一步，直至 former 走过链表 尾节点 时跳出（跳出后， latter 与尾节点距离为 k-1k−1，即 latter 指向倒数第 kk 个节点）。
4. 返回值： 返回 latter 即可

如下图所示：



代码如下：

class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        ListNode former = head, latter = head;
        for(int i = 0; i < k; i++)
            former = former.next;
        while(former != null) {
            former = former.next;
            latter = latter.next;
        }
        return latter;
    }
}

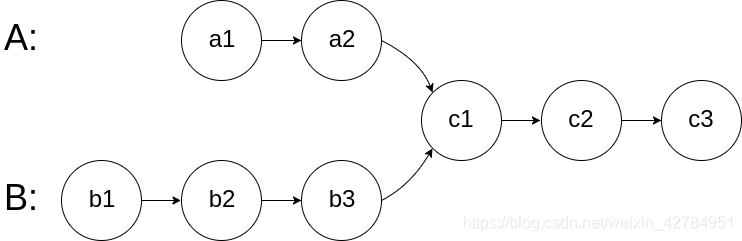
寻找两个链表交点问题

160. 相交链表

编写一个程序，找到两个单链表相交的起始节点。

如下面的两个链表：

• 创建两个指针 pA 和 pB，分别初始化为链表 A 和 B 的头结点。然后让它们向后逐结点遍历。
• 当 pA 到达链表的尾部时，将它重定位到链表 B 的头结点 (你没看错，就是链表 B); 类似的，当pB 到达链表的尾部时，将它重定位到链表 A 的头结点。 若在某一时刻 pA 和 pB 相遇，则 pA/pB 为相交结点。
• 想弄清楚为什么这样可行, 可以考虑以下两个链表: A={1,3,5,7,9,11} 和 B={2,4,9,11}，相交于结点 9。 由于 B.length (=4) < A.length (=6)，pB 比pA 少经过 22 个结点，会先到达尾部。将 pB 重定向到 A 的头结点，pA 重定向到 B 的头结点后，pB 要比pA 多走 2 个结点。因此，它们会同时到达交点。
• 如果两个链表存在相交，它们末尾的结点必然相同。因此当 pA/pB 到达链表结尾时，记录下链表 A/B对应的元素。若最后元素不相同，则两个链表不相交。

代码如下：

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        /**
        定义两个指针, 第一轮让两个到达末尾的节点指向另一个链表的头部, 最后如果相遇则为交点(在第一轮移动中恰好抹除了长度差)
        两个指针等于移动了相同的距离, 有交点就返回, 无交点就是各走了两条指针的长度
        **/
        if(headA == null || headB == null) return null;
        ListNode pA = headA, pB = headB;
        // 在这里第一轮体现在pA和pB第一次到达尾部会移向另一链表的表头, 而第二轮体现在如果pA或pB相交就返回交点, 不相交最后就是null==null
        while(pA != pB) {
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }
}