1.4 NUMERICAL TECHNIQUE: EULER’S METHOD
上一节中讨论的斜率场的几何概念与近似微分方程解的基本数值方法密切相关。给定一个初值问题
d y d t = f ( t , y ) , y ( t 0 ) = y 0 , \frac{dy}{dt}=f(t,y), \quad y(t_0) = y_0, dtdy=f(t,y),y(t0)=y0,
我们可以通过首先在 t y − ty- ty−平面上绘制斜率,然后从初始值 ( t 0 , y 0 ) (t_0,y_0) (t0,y0) 开始,通过绘制与斜率相切的图形来绘制解决方案的图形。沿着图形的每个点。在本节中,我们描述了一个自动化这个想法的数值过程。使用计算机或计算器,我们可以获得数字和图形,这些数字和图形可以近似解决初始值问题。
数值方法提供了关于解的定量信息,即使我们不能发现它们的公式。还有一个优点是大部分工作可以由机器完成。缺点是我们只能获得近似值,而不是精确解。如果我们仍然意识到这一事实并谨慎行事,那么数值方法将成为研究微分方程的强大工具。即使有可能找到解决方案的公式,也经常使用数值方法。(即使有公式,本文中的大多数微分方程解的图都是使用数值逼近绘制的。)
我们在本节中讨论的数值技术称为欧拉方法。关于欧拉方法以及其他数值方法的精度的更详细讨论将在第7章中给出。
沿斜率场逐步推进过程
为了描述欧拉方法,我们从初值问题开始
d y d t = f ( t , y ) , y ( t 0 ) = y 0 , \frac{dy}{dt}=f(t,y), \quad y(t_0) = y_0, dtdy=f(t,y),y(t0)=y0,
既然我们给定了 f ( t , y ) f (t,y) f(t,y),我们就可以在 t − y t-y t−y 平面上绘制它的斜率。该方法的想法是从斜坡场的点 ( t 0 , y 0 ) (t_0,y_0) (t0,y0) 开始,并采取由斜坡场的切线决定的微小步骤。我们首先选择一个 (小) 步长 Δ t \Delta t Δt。近似解的斜率每 Δ t \Delta t Δt 个单位更新一次。换句话说,对于每一步,我们沿着 t t t 轴移动 Δ t \Delta t Δt 个单位。
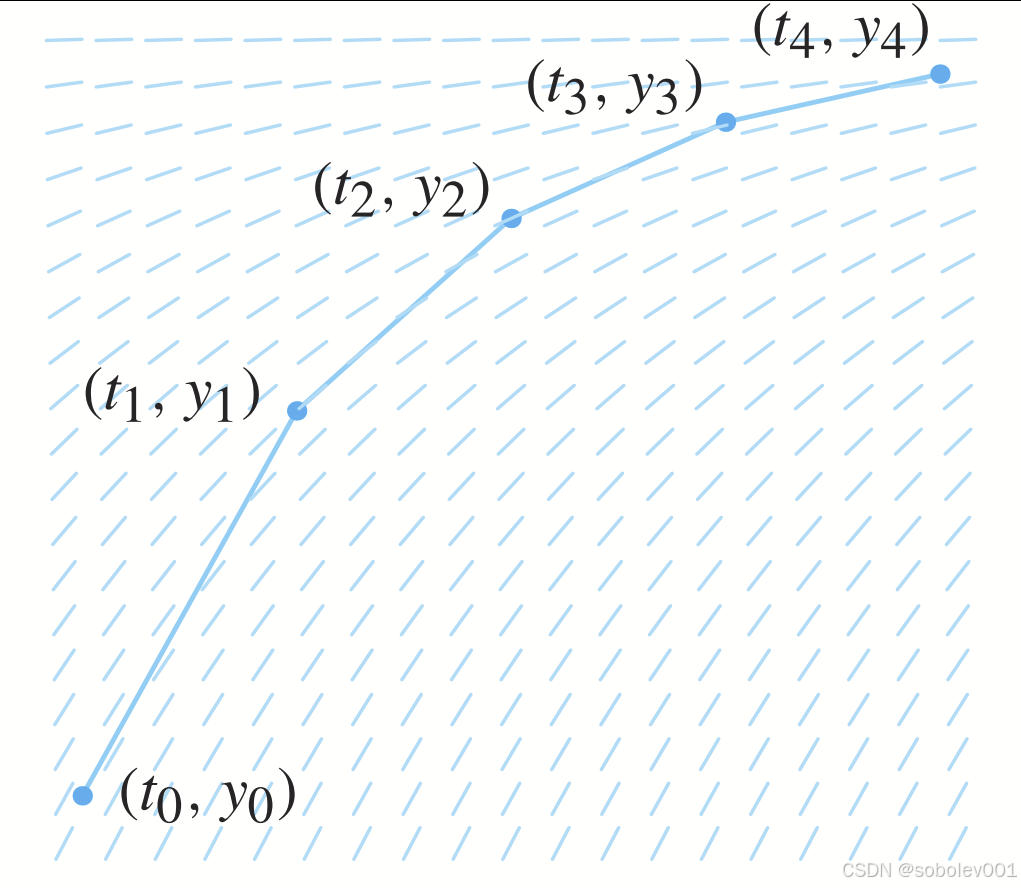
从 ( t 0 , y 0 ) (t_0, y_0) (t0,y0) 开始,我们的第一步是到达点 ( t 1 , y 1 ) (t_1, y_1) (t1,y1),其中 t 1 = t 0 + Δ t t_1 = t_0 + \Delta t t1=t0+Δt,并且 ( t 1 , y 1 ) (t_1, y_1) (t1,y1) 是通过 ( t 0 , y 0 ) (t_0, y_0) (t0,y0) 的直线上的点,其斜率由 ( t 0 , y 0 ) (t_0, y_0) (t0,y0) 的斜率场给出(见图1.31)。在 ( t 1 , y 1 ) (t_1, y_1) (t1,y1) 处,我们重复这一过程。沿着 t t t 轴的步长为 Δ t \Delta t Δt,其方向由 ( t 1 , y 1 ) (t_1, y_1) (t1,y1) 的斜率场确定,我们到达新点 ( t 2 , y 2 ) (t_2, y_2) (t2,y2)。新时间由 t 2 = t 1 + Δ t t_2 = t_1 + \Delta t t2=t1+Δt 给出, ( t 2 , y 2 ) (t_2, y_2) (t2,y2) 位于从 ( t 1 , y 1 ) (t_1, y_1) (t1,y1) 开始且斜率为 f ( t 1 , y 1 ) f(t_1, y_1) f(t1,y1) 的线段上。继续进行,我们使用点 ( t k , y k ) (t_k, y_k) (tk,yk) 的斜率场来确定下一个点 ( t k + 1 , y k + 1 ) (t_{k+1}, y_{k+1}) (tk+1,yk+1)。
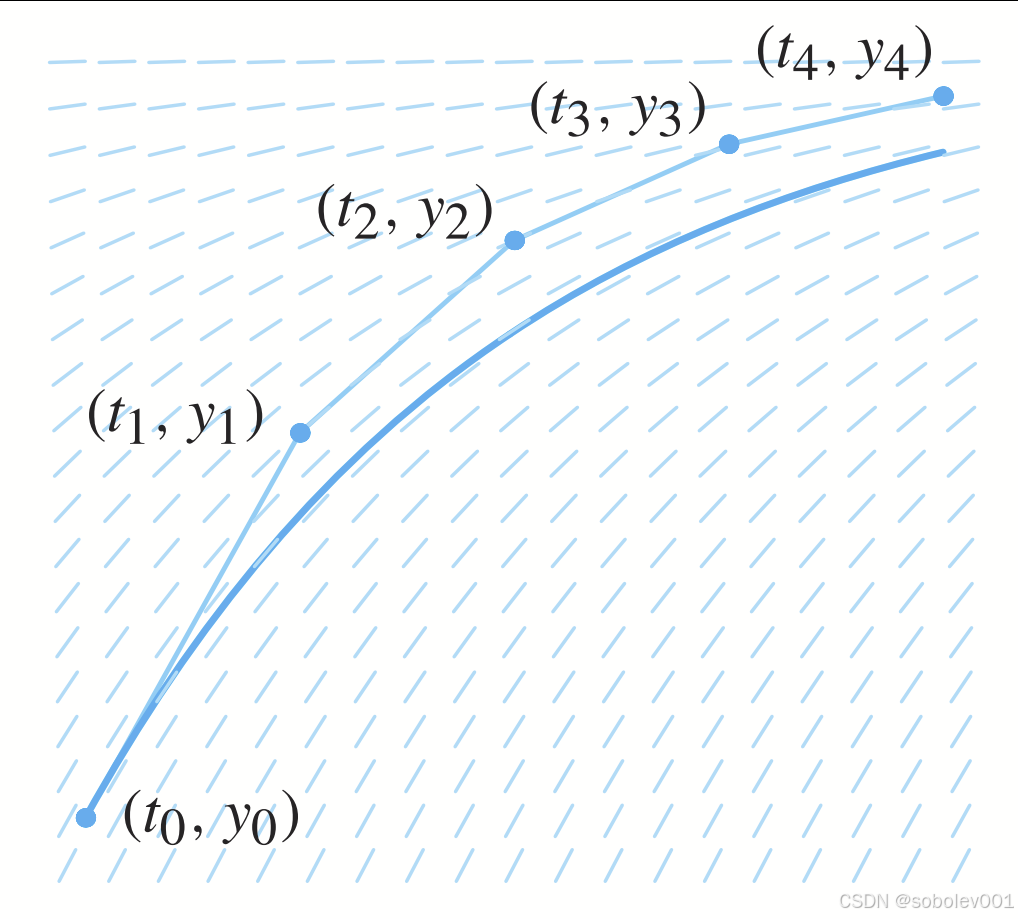
序列 y 0 , y 1 , y 2 , … y_0, y_1, y_2, \ldots y0,y1,y2,… 作为在时刻 t 0 , t 1 , t 2 , … t_0, t_1, t_2, \ldots t0,t1,t2,… 上解的近似值。从几何上讲,我们认为该方法是在连接 ( t k , y k ) (t_k, y_k) (tk,yk) 和 ( t k + 1 , y k + 1 ) (t_{k+1}, y_{k+1}) (tk+1,yk+1) 的一系列小线段(见图1.32)。基本上,我们将斜率场的小片段拼接在一起,形成一个近似我们的解曲线的图形。
该方法使用由斜率场给出的切线段来逼近解的图形。因此,在每个阶段,我们都会产生一个小误差(见图1.32)。希望如果步长足够小,这些误差在继续迭代时不会失控,且所得的图形接近于我们想要的解。
Euler 方法
为了将欧拉法付诸实践,我们需要一个公式由 ( t k , y k ) (t_k, y_k) (tk,yk) 确定 ( t k + 1 , y k + 1 ) (t_{k+1}, y_{k+1}) (tk+1,yk+1)。确定 t k + 1 t_{k+1} tk+1 很简单,我们在一开始就指定步长 Δ t \Delta t Δt,所以 t k + 1 = t k + Δ t