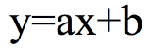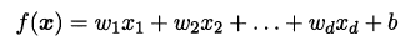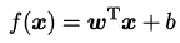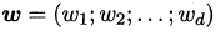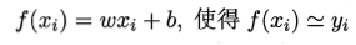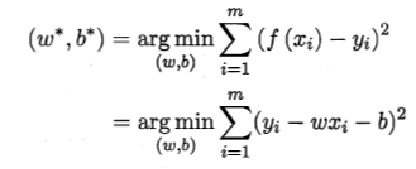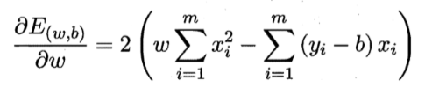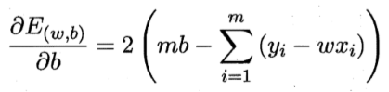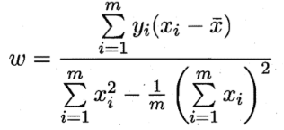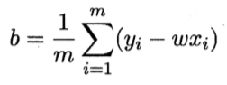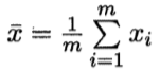机器学习线性回归模型

线性回归（linear regression）是一种线性模型，它假设输入变量 x 和单个输出变量 y 之间存在线性关系

具体来说，利用线性回归模型，可以从一组输入变量 x 的线性组合中，计算输出变量 y

给定有d个属性（特征）描述的示例 x =（x1; x2; …; xd），其中xi是x在第i个属性（特征）上的取值，线性模型（linear model）试图学得一个通过属性（特征）的线性组合来进行预测的函数，即：

一般用向量形式写成：

其中

• 假设特征和结果都满足线性，即不大于一次方。
• w和b学得之后，模型就得以确定。

许多功能更为强大的非线性模型可在线性模型的基础上通过引入层级结构或高维映射而得。

最小二乘法求解

基于均方误差最小化来进行模型求解的方法称为“最小二乘法”（least square method）

它的主要思想就是选择未知参数，使得理论值与观测值之差的平方和达到最小。

我们假设输入属性（特征）的数目只有一个：

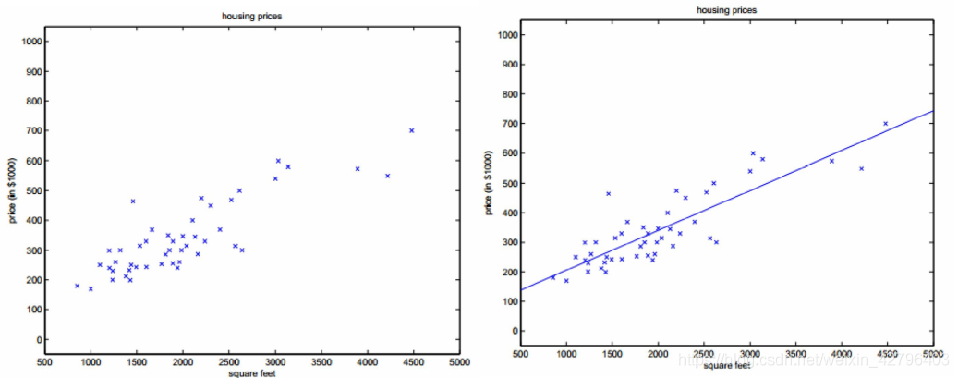
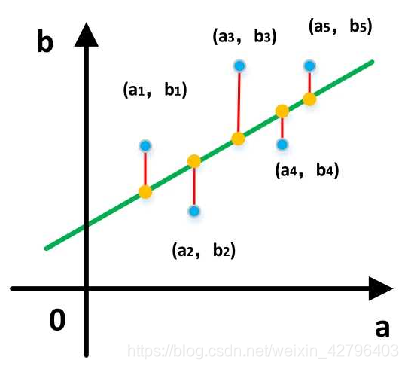
在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。

求解线性回归

求解w和b，使得 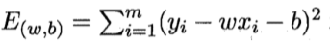最小化的过程，称为线性回归模型的“最小二乘参数估计”

将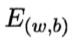分别对w和b求导，可以得到


令偏导数都为0，可以得到


—— 其中

代码实现

### 0.引入依赖
import numpy as np
import matplotlib.pyplot as plt

### 1.导入数据
points = np.genfromtxt('data.csv',delimiter=',')

points[0,0]

# 提取points中的两列数据，分别作为x,y
x = points[:, 0]
y = points[:, 1]

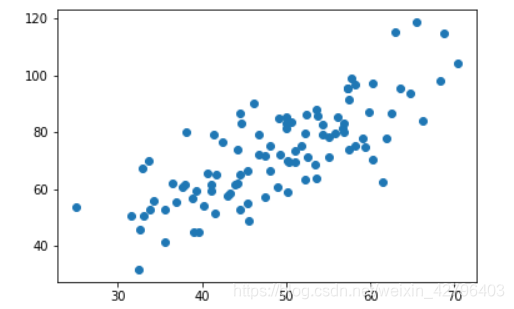
# 用plt画出散点图
plt.scatter(x, y)
plt.show()

###  2.定义损失函数
# 损失函数是系数的函数，另外还要传入数据的x，y
def compute_cost(w, b, points):
    total_cost = 0
    M = len(points)
    
    #逐点计算平方损失，然后计算平均值
    for i in range(M):
        x = points[i, 0]
        y = points[i, 1]
        total_cost += (y - w*x -b) ** 2

    return total_cost/M

### 3.定义算法拟合函数
# 先定义一个求均值的函数
def average(data):
    sum = 0
    num = len(data)
    for i in range(num):
        sum += data[i]
        
    return sum/num

 
# 定义核心拟合函数
def fit(points):
    M = len(points)
    x_bar = average(points[:,0])
    
    sum_yx = 0
    sum_x2 = 0
    sum_delta = 0
    
    for i in range(M):
        x = points[i, 0]
        y = points[i, 1]
        sum_yx += y * (x - x_bar)
        sum_x2 += x ** 2
    # 根据公式计算w
    w = sum_yx / (sum_x2 - M * (x_bar ** 2))
    
    for i in range(M):
        x = points[i, 0]
        y = points[i, 1]
        sum_delta += (y - w * x)
    b = sum_delta / M
    
    return w, b

### 4. 测试
w ,b = fit(points)

print("w is: ", w)
print("b is: ", b)

cost = compute_cost(w, b, points)

print("cost is : ",cost)


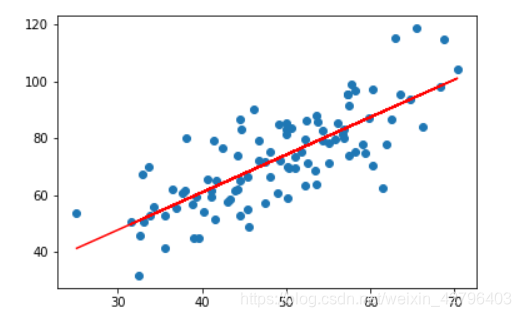
### 5.画出拟合曲线
plt.scatter(x,y)

#针对每一个x，计算得出预测的y值
pred_y = w * x + b

plt.plot(x, pred_y, c='r')
plt.show()