题目

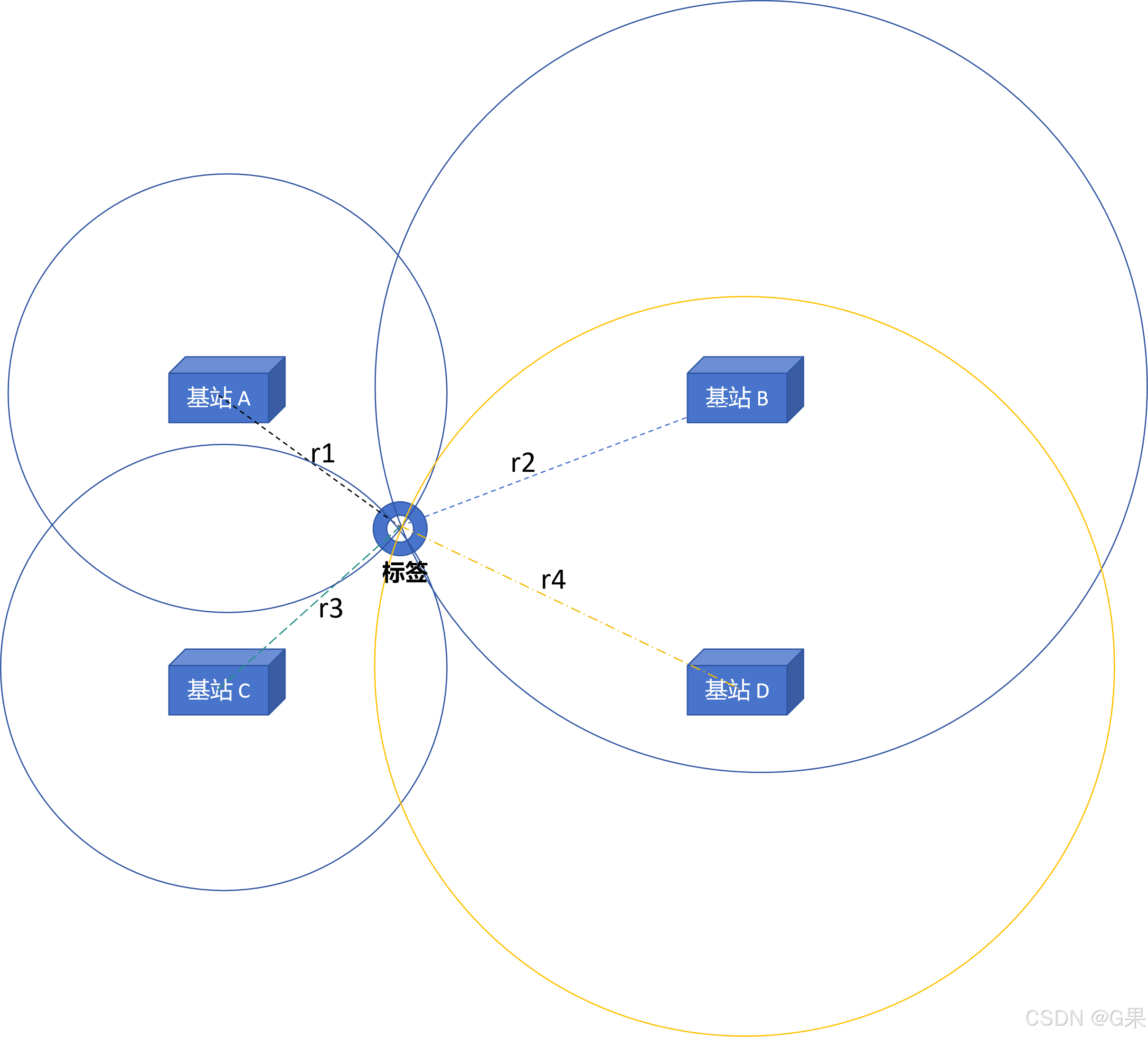
假设标签坐标为(x0,y0)，基站ABCD的坐标分别为(x1,y1)(x2,y2)(x3,y3)(x4,y4)，基站坐标已知，如何计算标签坐标？

三球交汇定理

三球交汇定位（ Three-ball intersection positioning schematic ）是一种基于几何原理的定位方法，通过已知的三个点（基站）和目标到这些点的距离来确定目标的位置。该方法在二维平面上进行，可以扩展到三维空间。题目中有4个基站，根据定理，选择三个基站进行方程计算即可。

计算过程

1. 距离方程：每个基站和标签之间的距离满足以下方程
   $$\begin{array}{rl}& {\left(x_n-x_0\right)}^2+\left(y_n-y_0\right)=r_n^2;其中n=1,2,3,4\end{array}$$

2. 转换方程：展开上述方程并简化，得到以下四个方程
   $$\begin{array}{rl}& x_0^2+y_0^2-2x_0{x}_1-2y_0{y}_1+x_1^2+y_1^2=r_1^2\\ & x_0^2+y_0^2-2x_0{x}_2-2y_0{y}_2+x_2^2+y_2^2=r_2^2\\ & x_0^2+y_0^2-2x_0{x}_3-2y_0{y}_3+x_3^2+y_3^2=r_3^2\\ & x_0^2+y_0^2-2x_0{x}_4-2y_0{y}_4+x_4^2+y_4^2=r_4^2\end{array}$$

3. 作差消元法：通过减去这些方程，消除 $x_0^2+y_0^2$ ，可以得到三个新的线性方程：

$$\begin{array}{rl}& -2x_0\left(x_1-x_2\right)-2y_0\left(y_1-y_2\right)=r_1^2-r_2^2+x_2^2+y_2^2-x_1^2-y_1^2\\ & -2x_0\left(x_1-x_3\right)-2y_0\left(y_1-y_3\right)=r_1^2-r_3^2+x_3^2+y_3^2-x_1^2-y_1^2\\ & -2x_0\left(x_1-x_4\right)-2y_0\left(y_1-y_4\right)=r_1^2-r_4^2+x_4^2+y_4^2-x_1^2-y_1^2\end{array}$$

4. 矩阵形式：提取 $x_0$ 和 $y_0$ 作为变量矩阵
   $$\left[\begin{array}{ll}{x}_1-x_2& y_1-y_2\\ x_1-x_3& y_1-y_3\\ x_1-x_4& y_1-y_4\end{array}\right]\left[\begin{array}{l}{x}_0\\ y_0\end{array}\right]=\frac{1}{2}\left[\begin{array}{l}{r}_1^2-r_2^2+x_2^2+y_2^2-x_1^2-y_1^2\\ r_1^2-r_3^2+x_3^2+y_3^2-x_1^2-y_1^2\\ r_1^2-r_4^2+x_4^2+y_4^2-x_1^2-y_1^2\end{array}\right]$$

代码实现

这个代码示例展示了如何通过球交汇定理计算标签的坐标。如果有四个基站数据，通常可以通过最小二乘法得到标签的坐标。

import numpy as np

def calculate_tag_position(x_coords, y_coords, distances):
    # 基站坐标
    x1, x2, x3, x4 = x_coords
    y1, y2, y3, y4 = y_coords
    r1, r2, r3, r4 = distances

    # 系数矩阵
    A = np.array([
        [x1 - x2, y1 - y2],
        [x1 - x3, y1 - y3],
        [x1 - x4, y1 - y4]
    ])

    # 常数项
    B = 0.5 * np.array([
        r1**2 - r2**2 + x2**2 + y2**2 - x1**2 - y1**2,
        r1**2 - r3**2 + x3**2 + y3**2 - x1**2 - y1**2,
        r1**2 - r4**2 + x4**2 + y4**2 - x1**2 - y1**2
    ])

    # 解方程 Ax = B
    pos, residuals, rank, s = np.linalg.lstsq(A, B, rcond=None)

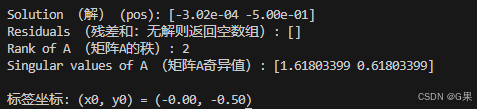
    print("\nSolution （解） (pos):", pos)
    print("Residuals （残差和：无解则返回空数组）:", residuals)
    print("Rank of A （矩阵A的秩）:", rank)
    print("Singular values of A （矩阵A奇异值）:", s)
        
    return pos


# 示例数据
x_coords = [0, 1, 0, 1]
y_coords = [0, 0, 1, 1]
distances = [1.0, 1.414, 1.0, 1.414]#距离

# 计算标签坐标
tag_position = calculate_tag_position(x_coords, y_coords, distances)
print(f"标签坐标: (x0, y0) = ({tag_position[0]:.2f}, {tag_position[1]:.2f})")

说明

1. x_coords 和 y_coords：基站的已知坐标。
2. distances：标签到每个基站的距离。
3. np.linalg.lstsq：使用最小二乘法求解方程组。（显然示例数据无解，求近似解使得distance的误差最小）
4. 上述代码举例是是用了4个基站的联立方程，结果用3基站的三球求解结果一样。

使用4个基站数据的结果：

使用3个基站数据的结果（注释 矩阵A的第二行 和 矩阵B的第二行）：