数据准备

创建lr_train_data.csv文件，内容如下

    x   y
   1   7
   2  10
   3  11
   4  12
   5  15
   6  16
   7  19
   8  22
   9  23
  10  24

读取数据

import pandas as pd
data = pd.read_csv('lr_train_data.csv')
x = data.loc[:,'x']
y = data.loc[:,'y']
print(type(x),type(y))

输出：<class 'pandas.core.series.Series'> <class 'pandas.core.series.Series'>

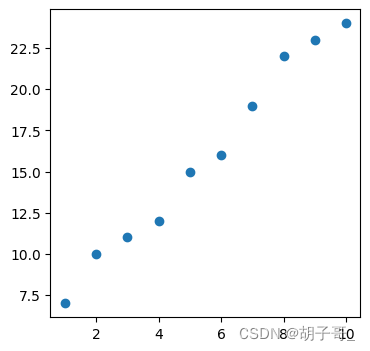
绘制图表（观察数据规律）

简单的一眼就看出来的可以省略此步骤

from matplotlib import pyplot as plt
plt.scatter(x,y)

从图可以看出明显的线性规律，可以设线性回归方程为：y=aX+b（训练完成后可以获得a,b的值，见下文）

数据处理

因为下面要使用sklearn的线性回归模型进行训练，而当前x数据结构是<class 'pandas.core.series.Series'>不符合要求(要求是二维数组)，需要先预处理数据。

import numpy as np
x = np.array(x)
x = x.reshape(-1,1)
print(type(x),x.shape)

输出：

<class 'numpy.ndarray'> (10, 1)
[[ 1]
 [ 2]
 [ 3]
 [ 4]
 [ 5]
 [ 6]
 [ 7]
 [ 8]
 [ 9]
 [10]]

这里为什么要处理成二维数组呢？可以这么理解，线性回归最简单的形式是：y=ax+b此处只有一个变量x，但更常见的是多个变量，比如：
y=aX1+bX2+cX3+d这种形式。所以这里二维数组的每行可以理解为一组X1,X2,X3的值。

模型训练

from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
lr_model.fit(x,y)
a = lr_model.coef_
b = lr_model.intercept_
print(a,b)

输出:

[1.94545455] 5.200000000000003

此处a值是一个数组，也是因为线性回归方程可能存在多个变量的缘故（每个变量前面有一个系数）。

预测

y_predict = lr_model.predict(x)
print(type(y_predict), y_predict)

输出：

<class 'numpy.ndarray'> [ 7.14545455  9.09090909 11.03636364 12.98181818 14.92727273 16.87272727
 18.81818182 20.76363636 22.70909091 24.65454545]

评估（MSE，R2）

from sklearn.metrics import mean_squared_error, r2_score
MSE = mean_squared_error(y,y_predict)
r2 = r2_score(y,y_predict)
print(MSE, r2)

输出：

0.46545454545454523 0.9853122579534697

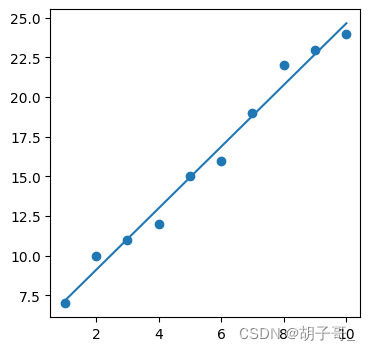
图形展示结果

from matplotlib import pyplot as plt
plt.plot(x,y_predict)
plt.scatter(x,y)