本人讲解关于slam一系列文章汇总链接:史上最全slam从零开始
有兴趣的朋友可以加微信 17575010159 相互讨论技术 - 文末公众号也可关注

一、前言

这篇博客，主要使用最通俗的语言来讲解SVD奇异值分解，通过该篇博客，将知道 SVD 的来龙去脉，底层原理。同时知道如何利用他去做图片压缩，PCA，求解矩阵(如 Fundamental 矩阵，Homography 矩阵)等。我会详细的讲解 SVD 的每一个细节。由浅到深，由窄到广。那么我们现在就开始吧。

二、简单原理介绍

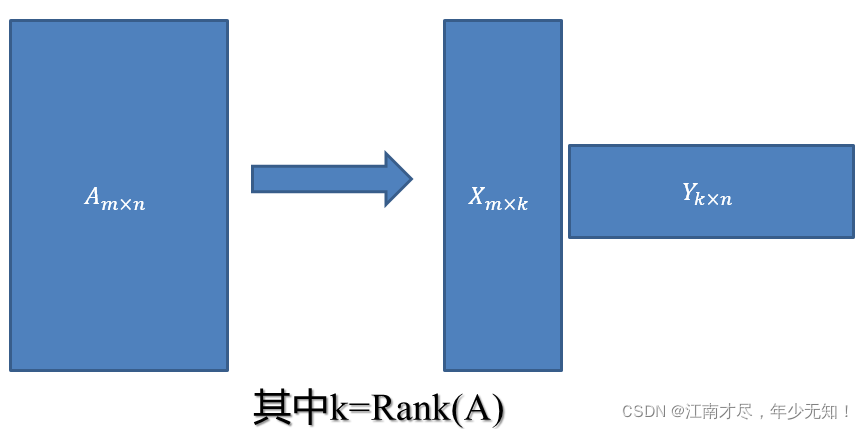
在推导数学公式，以及几何意义之前，我们先来看看其物理层面的应用。这样有助于后面更深层次的理解。首先这里有个基本的概念简单说一下, 一个 $m\times n$ 维的矩阵，我们可以分解成 $m\times k$ 以及 $k\times n$ 的矩阵相乘，如下图所示：

到了这一步还不够，我们还要继续分解，根据上面的原理，我们是不是可以对矩阵 $X_{m\times k}$ 做同样的分解，把他分解成两个矩阵。那么我们现在来做个假设(后面有推导该公式的细节以及计算过程)：
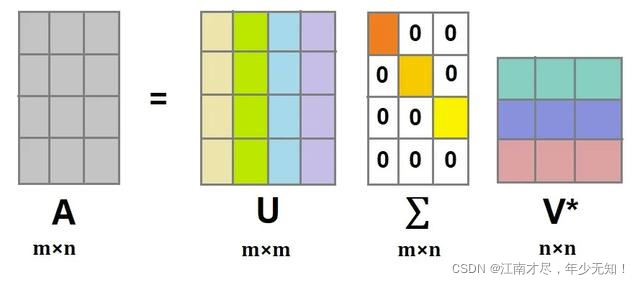
$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\text{\hspace{1em}(1)}$$其下标$m\times m,m\times m,n\times n$ 分别表示对应形状。大家可能比较奇怪了，把一个矩阵分解成这个样子，有什么作用。如果矩阵 $A_{m\times m}$ 使用其上三个矩阵来表示，似乎并没有节省空间。这个先不着急，继续往下分析，如果公式(1)中的具备如下特征：

对于 $m$ 行 $n$ 列的矩阵 $A$, 通过SVD分解之后，拆分成了3个子矩阵，其中 $U$ 矩阵为 $m$ 行 $m$ 列的方阵，$V$ 为 $n$ 行 $n$ 列的方阵，$\Sigma$为只有对角线有值的矩阵，其中的值称之为奇异值。看一个例子，原始矩阵如下:$$A_{4\times 5}=\left[\begin{array}{lllll}1& 0& 0& 0& 2\\ 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{array}\right]\text{\hspace{1em}(2)}$$奇异值分解的结果如下$$U_{4\times 4}=\left[\begin{array}{llll}0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\end{array}\right],{\Sigma }_{4\times 5}=\left[\begin{array}{ccccc}4& 0& 0& 0& 0\\ 0& 3& 0& 0& 0\\ 0& 0& \sqrt{5}& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right],V_{5\times 5}^T=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ \sqrt{0.2}& 0& 0& 0& \sqrt{0.8}\\ 0& 0& 0& 1& 0\\ \sqrt{0.8}& 0& 0& 0& -\sqrt{0.2}\end{array}\right]\text{\hspace{1em}(3)}$$
在奇异值分解中，$\Sigma$ 矩阵的奇异值是按照从大到小的顺序排列的，而且减少的特别快，经常前 10% 的奇异值就占据了全部奇异值 99% 以上的比例。基于这个性质，我们可以只提取前几个奇异值及其对应的矩阵来近似的描述原来的矩阵。

那么我们现在就来做个实验，我们只获取矩阵得如下部分来复原矩阵 $A$:

也就是
$$U_{4\times 3}=\left[\begin{array}{lll}0& 0& 1\\ 0& 1& 0\\ 0& 0& 0\\ 1& 0& 0\end{array}\right],{\Sigma }_{3\times 3}=\left[\begin{array}{ccc}4& 0& 0\\ 0& 3& 0\\ 0& 0& \sqrt{5}\end{array}\right],V_{3\times 5}^T=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ \sqrt{0.2}& 0& 0& 0& \sqrt{0.8}\end{array}\right]\text{\hspace{1em}(4)}$$这样就是然后我们求得 $A_{4\times 5}=U_{4\times 3}{\Sigma }_{3\times 3}{V}_{3\times 5}^T$,其结果如下：
$$A_{4\times 5}=\left[\begin{array}{lllll}1& 0& 0& 0& 2\\ 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{array}\right]\text{\hspace{1em}(5)}$$可以看到其与(2)式中的 $A_{4\times 5}$ 结果是完全一致的，完成了完美的复原。为什么这里能完成完美的复原呢? 因为 $\Sigma$ 矩阵的奇异值表示其对应的 $特征(后面有详细讲解)$ 重要性，其因为 ${\Sigma }_{3\times 3}$ 已经包含了 ${\Sigma }_{4\times 5}$ 的所有非零元素，所以其是可以完美复原出来的。现在我们来看看，其他的不同矩阵取值，如下图所示：

也就是
$$U_{4\times 2}=\left[\begin{array}{ll}0& 0\\ 0& 1\\ 0& 0\\ 1& 0\end{array}\right],{\Sigma }_{3\times 3}=\left[\begin{array}{cc}4& 0\\ & \\ & \\ 0& 3\end{array}\right],V_{3\times 5}^T=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ & & & & \\ 0& 0& 1& 0& 0\end{array}\right]\text{\hspace{1em}(6)}$$这样就是然后我们求得 $A_{4\times 5}=U_{4\times 2}{\Sigma }_{3\times 3}{V}_{2\times 5}^T$,其结果如下：$$A_{4\times 5}=\left[\begin{array}{lllll}0& 0& 0& 0& 0\\ 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{array}\right]\text{\hspace{1em}(7)}$$这个时候我们与前面 (2) 式 $A_{4\times 5}$ 相比，可以发现其第1行的第4列与第4列的两个1，已经不见了。也就是说明其复原过程中出现了信息丢失。上面的两个实验可以总结如下图所示:

上图主要表示了如下公式($k$与$n$越接近说明图像还原度越高，当然压缩效果也没有那么明显): $$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T\text{\hspace{1em}(8)}$$

三、图像压缩

那么我们如何使用 SVD 来做图像压缩呢? 通过上面的介绍，我们就可以完成图像压缩了。这里我们把一张图像的像素看作前面的矩阵$A_{m\times n}$，然后编写代码如下：

import cv2
import numpy as np
# 调整该值重复运行代码保存图像
k = 200
img = cv2.imdecode(np.fromfile('./1.png', dtype=np.uint8), 0)
u, w, v = np.linalg.svd(img)
u = u[:, :k]
w = np.diag(w)
w = w[:k, :k]
v = v[:k, :]
img = u.dot(w).dot(v)
cv2.imencode('.jpg', img)[1].tofile('k={}.jpg'.format(k))

调整代码中的 $k$ 值，重复保存图像。注意，根据前面的介绍我们可以得知 $0<k<h$, k值越大，图像的还原度越高。原图如下：

本人调整 $k=100$, $k=50$, $k=20$值保存结果如下：

我们输入一张图像，通过SVD奇异值分解分解之后，得到 u, w, v 三个矩阵，根据自己的需求，对这三个矩阵进行适当的剪切，代码中的剪切大小通过变量 $k$ 控制。我们只需要保存剪切之后的矩阵，就可以复原图像了。注意这里的 w 为对角矩阵，只需要保存对角线的元素即可。

那么我们来计算一下，这张图像压缩多少空间。因为上图中我们可以看到 $k=100$ 的时候，图像基本是没有太大损失的。所以我们按 $k=100$ 来计算。原始图像像素为200x200=40000。压缩之后为 200x100+100+100x100=20000+100+10000=30100。可以看到其压缩了1/4左右的大小，并且基本没有像素损失。

四、特征值分解→EVD

两个矩阵 $A$$B$ 相乘, 其为$A$ 的行与 $B$ 的列，对应相乘相加，所以出现如下公式:$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\text{\hspace{1em}(1)}$$通过前面介绍我们知道 $\Sigma$ 为只有对角线有值的矩阵，其中的值称之为奇异值。奇异值表示其对应 $特征$ 的重要性。在对齐讲解之前，我们需要回顾一下特征值与特征向量,首先其定义如下：
$$A\vec{x}=\lambda \vec{x}\text{\hspace{1em}(9)}$$ 其中 $A$ 为 $m\times m$的方阵 $方阵$(该前置条件)， $\vec{x}$ 是一个 $m$ 维的列向量，满足上诉公式，则我们说 $\lambda$ 是矩阵 $A$ 的一个特征值，而 $\vec{x}$ 是矩阵 $A$ 的特征值在 $\lambda$ 所对应的特征向量。为什么可以写成这个样子，主要是因为：

	1、矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。
	
	2、如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，
	那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。

如果想稍微了解具体一点的，可以参考一下这篇博客:特征值与特征向量的意义。一个矩阵有多个相互对应的 $\vec{x}$ 与 $\lambda$ 。那么我们写成一个通用式子:$$A\overrightarrow{x_i}={\lambda }_i\vec{x}\text{\hspace{1em}(10)}$$一个 $m$ 阶的方阵，那么则有：$$\begin{array}{rl}A\overrightarrow{x_1}& ={\lambda }_1\overrightarrow{x_1}\\ A\overrightarrow{x_2}& ={\lambda }_2\overrightarrow{x_2}\\ & \cdots \\ A{\vec{x}}_m& ={\lambda }_m{\vec{x}}_m\end{array}\text{\hspace{1em}(11)}$$这里我们令:$$U_{m\times m}=[\overrightarrow{x_1}\overrightarrow{x_2}\overrightarrow{x_3}\cdots \overrightarrow{x_m}]$$$$\Lambda =\left[\begin{array}{ccc}{\lambda }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\lambda }_m\end{array}\right]$$则我们可以得到$$AU=U\Lambda \text{\hspace{1em}(12)}$$进一步推导（由于这里的特征向量两两正交，所以U为正交阵，正交阵的逆矩阵等于其转置-有兴趣的同学可以百度一下正交矩阵）：$$A=U\Lambda U^{-1}=U\Lambda U^T\text{\hspace{1em}(13)}$$到这里为止，对于方阵的特征分解可以说是完成了。但是这里出现了一个问题，上面的结论是基于$方阵$推导出来的，那么如果 $A$ 并非一个方阵，而是一个任意的矩阵呢? 比如前面提到的$A_{m\times n}$ 或者张长方形的图像。那么就无法 EVD 特征分解了。这个时候就轮到 SVD 奇异值分解登场了。

五、特征值分解→SVD

通过前面的介绍，我们知道知道一个方阵是可以进行 EVD 特征分解的，经过推导得到公式(13)
$$A_{m\times m}=U\Lambda U^{-1}=U\Lambda U^T\text{\hspace{1em}(13)}$$那么一个矩形的矩阵如$A_{m\times n}$我们如何进行分解呢? 首先我们可以把 $A_{m\times n}$ 转换成 $m\times m$ 的或者 $n\times n$ 矩阵，那么我们就可以使用 EVD 进行分解了，比如 $A{A}^T$ 与 $A^{T}A$ 分别会得到 $m\times m$， $n\times n$ 的矩阵。我们回顾一下 SVD 奇异值分解公式：$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\text{\hspace{1em}(1)}$$
$注意[$ 其中 $U$ 是一个 $m\times m$ 的矩阵，$\Sigma$ 是一个 $m\times n$ 的矩阵，除了主对角线上的元素以外全为 0，主对角线上的每个元素都称为奇异值，$V$ 是一个 $n\times n$ 的矩阵。$U$ 和 $V$ 都是酉矩阵(有兴趣的朋友可以百度一下)，即满足 $U^{T}U=E$，$V^{T}V=E$，这里的 $E$ 表示单位矩阵，即对角线为1，其余都是0的矩阵$]$

如果我们将 $A$ 的转置和 $A$ 做矩阵乘法，那么会得到 $n\times n$ 的一个方阵$A^{T}A$。既然 $A^{T}A$ 是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：$$\left(A^{T}A\right){\vec{v}}_i={\lambda }_i{\vec{v}}_i$$

这样我们就可以得到矩阵 $A^{T}A$ 的 $n$ 个特征值和对应的 $n$ 个特征向量 $\vec{v}$。将$A^{T}A$ 的所有特征向量张成一个n×n的矩阵 $V$，就是我们SVD公式里面的 $V$ 矩阵了。一般我们将 $V$ 中的每个特征向量叫做A的右奇异向量。

如果我们将 $A$ 和 $A$ 的转置做矩阵乘法，那么会得到 $m\times m$ 的一个方阵$A{A}^T$ 既然是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：$$\left(A{A}^T\right){\vec{u}}_i={\lambda }_i{\vec{u}}_i$$这样我们就可以得到矩阵 $A{A}^T$ 的m个特征值和对应的m个特征向量 $\vec{u}$了。将 $A{A}^T$ 的所有特征向量张成一个 $m\times m$ 的矩阵 $U$，就是我们SVD公式里面的 $U$ 矩阵了。一般我们将 $U$ 中的每个特征向量叫做 $A$ 的左奇异向量。

$U$ 和 $V$ 我们都求出来了，现在就剩下奇异值矩阵 $\Sigma$ 没有求出了。由于 $\Sigma$ 除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值 $\sigma$ 就可以了(后面有举例如何求解)。我们注意到:$$A=U\Sigma V^T\Rightarrow AV=U\Sigma V^{T}V\Rightarrow AV=U\Sigma \Rightarrow A{v}_i={\sigma }_i{u}_i\Rightarrow {\sigma }_i=A{v}_i/u_i$$其上的 ${\sigma }_i$ 就是每个特征对应的奇异值，那么进而求出出奇异值矩阵 $\Sigma$。

上面还有一个问题没有讲，就是我们说 $A^{T}A$ 的特征向量组成SVD中的 $V$ 矩阵，而 $A{A}^T$ 的特征向量组成SVD中的 $U$ 矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例(用到：$U^{T}U=I,{\Sigma }^T\Sigma ={\Sigma }^2$)。$$A=U\Sigma V^T\Rightarrow A^T=V{\Sigma }^T{U}^T\Rightarrow A^{T}A=V{\Sigma }^T{U}^{T}U\Sigma V^T=V{\Sigma }^2{V}^T\text{\hspace{1em}(14)}$$可以看出(根据公式13) $A^{T}A$ 特征向量组成 SVD 中的 $V$ 矩阵。类似的方法可以得到 $A{A}^T$ 的特征向量组成 SVD 中的 $U$ 矩阵。进一步我们还可以看出特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：$${\sigma }_i=\sqrt{\lambda }$$这样也就是说，我们可以不用 ${\sigma }_i=A{v}_i/u_i$来计算奇异值，也可以通过求出$A^{T}A$的特征值取平方根来求奇异值。如果大家看到这里来，比较蒙圈了，我们就来看一个例子吧。

七、SVD 计算举例

这里我们用一个简单的例子来说明矩阵是如何进行奇异值分解的。我们的矩阵A定义为：$$A=\left[\begin{array}{cc}1& 1\\ 1& 1\\ 1& 0\end{array}\right]$$我们首先求出$A^{T}A$，$A{A}^T$:
$$A^{T}A=\left[\begin{array}{ccc}0& 1& 1\\ & & \\ 1& 1& 0\end{array}\right]\left[\begin{array}{cc}0& 1\\ 1& 1\\ 1& 1\end{array}\right]=\left[\begin{array}{cc}2& 1\\ & \\ 1& 2\end{array}\right]\text{\hspace{1em}(14)}$$$$A{A}^T=\left[\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 1\\ & & \\ 1& 1& 0\end{array}\right]=\left[\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right]\text{\hspace{1em}(15)}$$然后我们还需要求得 $A^{T}A$ 的特征向量值与特征向量, 先来回顾一下矩阵特征值和特征向量的计算过程：$A$ 为 m 阶矩阵，若数 $\lambda$ 和 $m$ 维非 0 列向量 $\vec{x}$ 满足 $A\vec{x}=\lambda \vec{x}$，那么数 $\lambda$ 称为 $A$ 的特征值，$\vec{x}$ 称为 $A$ 的对应于特征值λ的特征向量。式 $A\vec{x}=\lambda \vec{x}$ 也可写成 $(A-\lambda E)\vec{x}=0$，并且 $|\lambda E-A|$ 叫做A 的特征多项式。当特征多项式等于0的时候，称为 $A$ 的特征方程，特征方程是一个齐次线性方程组，求解特征值的过程其实就是求解特征方程的解。推导细节如下（其中的 $E$ 为单位矩阵，即对角线为1，其余都为0的矩阵）：$$A\vec{x}=\lambda \vec{x}\Rightarrow A\vec{x}=\lambda E\vec{x}\Rightarrow (\lambda E-A)\vec{x}=0$$$$|\lambda E-A|=\left[\begin{array}{cccc}\lambda -a_{11}& -a_{12}& \cdots & -a_{1n}\\ -a_{21}& \lambda -a_{22}& \cdots & -a_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ -a_{m1}& -a_{m2}& \cdots & \lambda -a_{mn}\end{array}\right]=0$$也就是$|\lambda E-A|$ 对应的行列式为0即可。根据上述公式我们可以求解出出$A{A}^T$的特征值与特征：

$${\lambda }_1=3,v_1=\left[\begin{array}{c}1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6}\end{array}\right];{\lambda }_2=1,v_2=\left[\begin{array}{c}1/\sqrt{2}\\ 0\\ -1/\sqrt{2}\end{array}\right];{\lambda }_3=0,v_3=\left[\begin{array}{c}1/\sqrt{3}\\ -1\sqrt{3}\\ 1/\sqrt{3}\end{array}\right];$$利用${\sigma }_i=A{v}_i/u_i$ 其中 $i=1,2$ 求奇异值的：$$A=U\Sigma V^T=\left(\begin{array}{ccc}1/\sqrt{6}& 1/\sqrt{2}& 1/\sqrt{3}\\ 2/\sqrt{6}& 0& -1/\sqrt{3}\\ 1/\sqrt{6}& -1/\sqrt{2}& 1/\sqrt{3}\end{array}\right)\left(\begin{array}{cc}\sqrt{3}& 0\\ 0& 1\\ 0& 0\end{array}\right)\left(\begin{array}{cc}1/\sqrt{2}& 1/\sqrt{2}\\ -1/\sqrt{2}& 1/\sqrt{2}\end{array}\right)$$

六、结语

通过该篇博客，我们知道了如何对一个矩阵进行 SVD 奇异值分解，并且列举了一个图像压缩的例子。但是这仅仅其中的一部分应用，我们还可以用来求解超定方程 $Ax=0$(最优解)。 当然，该博客的篇幅已经很长了，所以令起一篇博客继续为大家介绍如何求解超定方程，为什么最小奇异值对应的特征值，为超定方程的解。