二叉树的创建和遍历实现

1 前言

提到**树（Tree）**结构，很容易联想到”大树“，想到这是“一对多关系“特性的数据结构，其相关的名词、概念很多：

子树（SubTree）、结点（Node）、根结点（Root）、叶子（Leaf）/ 终端结点、分支结点 / 非终端结点、内部结点、孩子（Child）、双亲（Parent）、兄弟（Sibling）、堂兄弟、祖先、子孙
层次（Level）、度（Degree）、深度（Depth）/ 高度
空树、有序树、只有根结点的树、普通树、二叉树、斜树、满二叉树、完全二叉树等等

这里对于这些个概念不再一一展开介绍，对以上名词陌生的小伙伴可以自行学习。可参考：二叉树的相关概念

2 二叉树

首先得是颗树，然后是他的节点是两个，限制了分叉数量2。

2.1 顺序储存（数组实现）

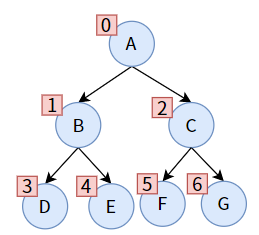
图示为一颗满二叉树，我们按照层次（Level）从0-n（数组下标）进行编号，这样就可以储存二叉树了。
犯得上发射点

char* arr;
arr[0] = 'A';
arr[1] = 'B';
arr[2] = 'C';
arr[3] = 'D';
arr[4] = 'E';
arr[5] = 'F';
arr[6] = 'G';

这样我们便可以使用数组存储二叉树了。
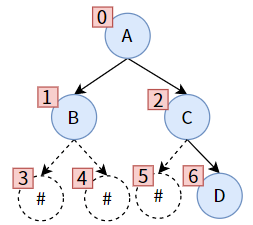
如果对于一个普通二叉树呢？可以构造出一个满/完全二叉树，对于虚构得节点用’#‘代替。如下一颗普通二叉树，用#补成满二叉树。
在这里插入图片描述

char* arr;
arr[0] = 'A';
arr[1] = 'B';
arr[2] = 'C';
arr[3] = '#';
arr[4] = '#';
arr[5] = '#';
arr[6] = 'G';

这里的问题是，将浪费内存，极端点，如果变成了右斜树，顺序储存将浪费大量空间。

2.2 链式储存（链表实现）

链表对我们来说并不陌生，通过结点加箭头的方式来存储数据，节点表示数据元素，箭头表示节点间的关系。
那二叉树的链式结构应该什么样呢？在开始就说二叉树是只有两个分叉的树，那么很简单，二叉树由一个的节点和两个分支组成，即：

数据元素
左子树分支（结点的左孩子）
右子树分支（结点的右孩子）
那现在这个结构就很显然了

/*二叉树的结点的结构体*/
typedef struct BiTNode {
    char data; //数据域
    struct BiTNode *lchild; //左孩子指针
    struct BiTNode *rchild; //右孩子指针
} BiTNode, *BiTree;;

实际上二叉链表是比较常用的存储方式，当然也可以在结构中加入struct BiTNode *parent；可以很轻松地找到各节点的父节点，这时的链表可以称为三叉链表。

2.3二叉树的创建

二叉树百科中递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。
既然二叉树是通过递归定义的，所以想要创建一颗二叉树，这里可以借助递归去创造。
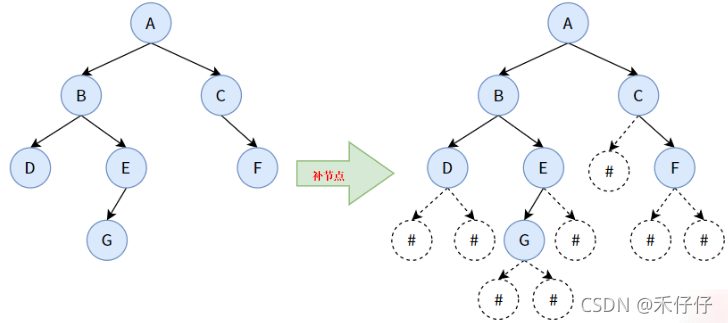
前面在构建顺序链表时，将普通二叉树补全成满/完全二叉树。这里当拿到一颗普通二叉树时，能迅速将其个节点内容补齐，如下：
在这里插入图片描述
这里使用“#”代替“NULL”，补全子节点、叶节点的结构，而NULL(#)节点是不指向任何节点的。
我们通过先序遍历的方法输出下补充后的二叉树，即为：ABD##EG###C#F##，同样也可以中序遍历，或者后序遍历像这样输出节点，只需对创建函数对应修改即可。
按照前序遍历的顺序创建二叉树，代码如下：

void CreateBiTree(BiTree *T)
{
    char ch;
    scanf("%c",&ch);
    if (ch == '#')
        *T = NULL;  //保证是叶结点
    else
    {
        *T = (BiTree)malloc(sizeof(BiTNode));
        if (!*T) return;
        (*T)->data = ch;//生成结点
        CreateBiTree(&(*T)->lchild);//构造左子树
        CreateBiTree(&(*T)->rchild);//构造右子树    
    }
}

值得注意的是，CreateBiTree(BiTree *T)，的入参是二级指针。一级指针不行嘛，遍历时用的都是一级指针，学生时代并没太注意，只是记下了，稍后代码说明。

这里使用的递归创建和前序遍历是一致的。

3 二叉树遍历

3.1递归实现

前面进行二叉树创建就是根据二叉树的定义，通过递归实现了二叉树的创建，当然遍历也是如此，无非就三件事：访问根结点、找左子树、找右子树。

先序遍历

/*
*先序遍历
*root：指向根根节点的指针
*/
void preOrderTranversal(BiTNode *root){
    if(root == NULL) return;//节点（根或者子根节点）
    printf("%c\t",root->data);
    preOrderTranversal(root->lchild);//遍历左子树
    preOrderTranversal(root->rchild);//遍历右子树
}

中序遍历


/*中序遍历*/
void inorder_traversal(BiTNode *root)
{
    if (root == NULL) { //若二叉树为空，做空操作
        return;
    }
    inorder_traversal(root->lchild); //递归遍历左子树
    printf("%c\t", root->data); //访问根结点
    inorder_traversal(root->rchild); //递归遍历右子树
}

后续遍历

/*后序遍历*/
void postorder_traversal(BiTNode *root)
{
    if (root == NULL) { //若二叉树为空，做空操作
        return;
    }
    postorder_traversal(root->lchild); //递归遍历左子树
    postorder_traversal(root->rchild); //递归遍历右子树
    printf("%c\t", root->data); //访问根结点
}

main函数

void main(void){
    BiTree T = NULL;
    CreateBiTree(&T);
    printf("先序遍历：");
    preOrderTranversal(T);
    printf("\n");

    printf("中序遍历：");
    inorder_traversal(T);
    printf("\n");

    printf("后序遍历：");
    postorder_traversal(T);
    printf("\n");
}

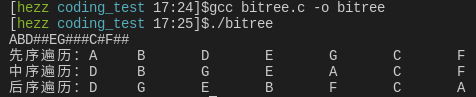
执行下看看：
在这里插入图片描述

4 栈实现二叉树遍历

代码不再这里粘贴了，另外不仅栈，队列也可以实现二叉树的遍历。
想学习的小伙伴可参考，栈实现二叉树的遍历

*为什么创建二叉树时使用二级指针做入参

请看下面代码：

#include <stdio.h>

//目标：在函数func中将b赋值给*q;
int a= 10;
int b = 100;
int *q;

void func(int *p){
    printf("fun:&p = %p p = %p\n",&p,p);
    p = &b;
    printf("fun:&p = %p p = %p\n",&p,p);
}

int main(){
    printf("&a = %p &b = %p &q = %p\n",&a,&b,&q);
    q = &a;
    printf("*q = %d q = %p &q = %p\n",*q,q,&q);
    func(q);
    printf("*q = %d q = %p &q = %p\n",*q,q,&q);
    return 0;
}

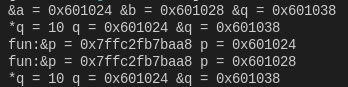
乍一看去，好像没有问题，我们将指针q传入函数func，那好先运行一下看看结果如下：
在这里插入图片描述
我们并没有成功将q指向b，这里为什么呢？
因为func的入参是q，即进入的参数是&a，然后在func起来后，在堆栈申请内存，将b的值放入该地址，但返回时也将销毁。
我们可以通过二级指针才操作，具体如下：
func()入参改为二级指针，入参为&q的地址

void func(int **p){
    printf("fun:&p = %p p = %p\n",&p,p);
    *p = &b;//改变q指向的内容
    printf("fun:&p = %p p = %p\n",&p,p);
}

int main(){
    printf("&a = %p &b = %p &q = %p\n",&a,&b,&q);
    q = &a;
    printf("*q = %d q = %p &q = %p\n",*q,q,&q);
    func(&q);
    printf("*q = %d q = %p &q = %p\n",*q,q,&q);
    return 0;
}

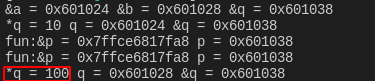
在这里插入图片描述
此时，将可以修改q指向的内容。我写的有点乱，可以拿笔画一画简单体会下。哈哈哈~

参考

https://www.jianshu.com/p/12848eef3452
https://cloud.tencent.com/developer/article/1819521
https://blog.csdn.net/lingling_nice/article/details/80960439