0. 作业要求

1. 概述

1.1 背景知识

1.1.1 数字传输系统

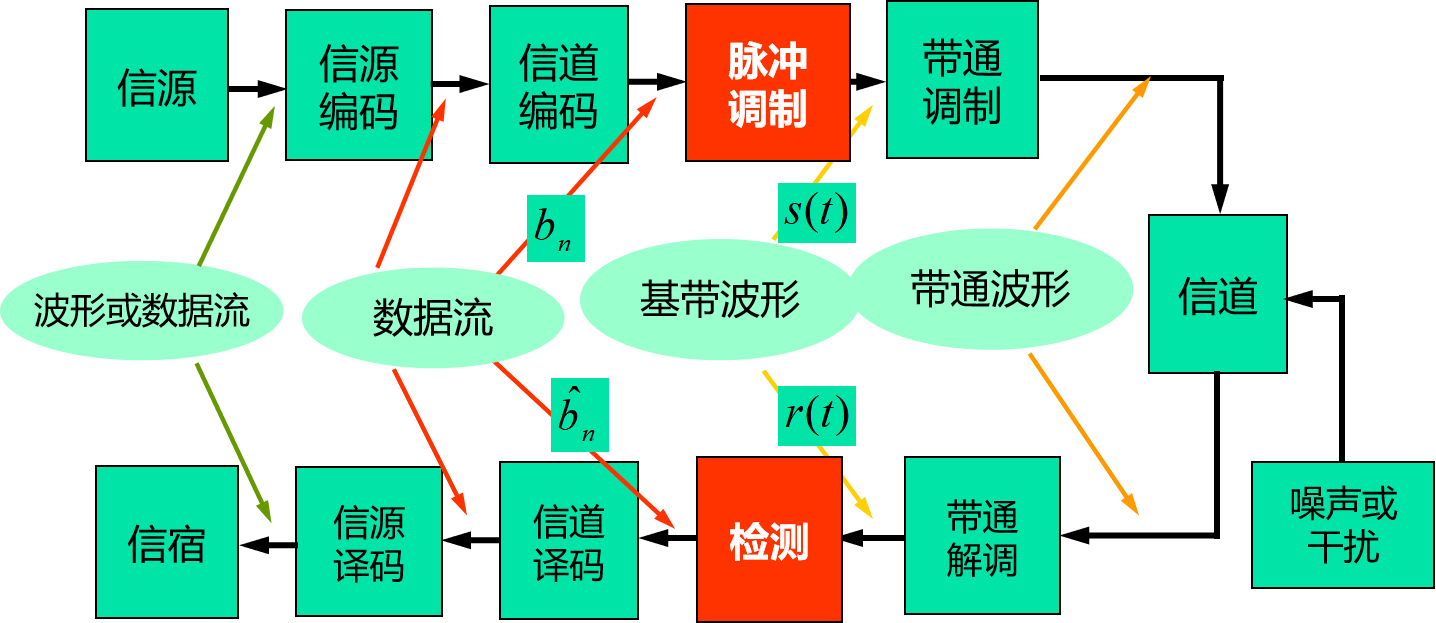
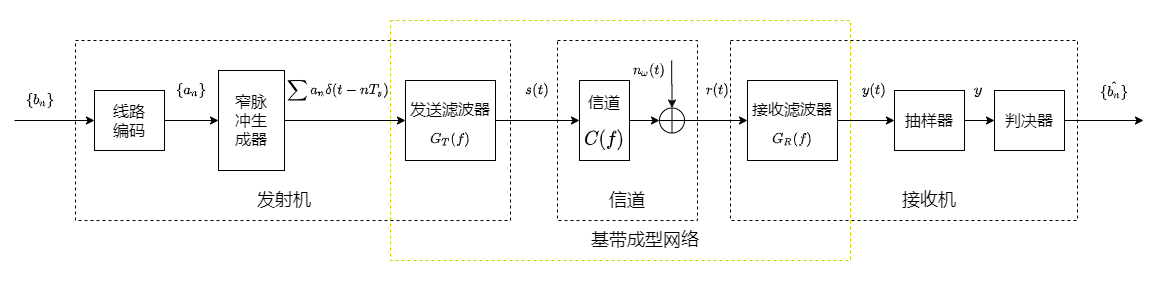
数字传输系统通用模型如下图所示

• 信源: 信源是消息的来源, 输出的是消息(或符号), 一般需要将其转换为电信号输出
• 信源编码: 信源编码是对信源输出的电信号用尽量低速率的二进制数字信号表示, 减少消息剩余度, 输出二进制数字序列(信息序列)
• 信道编码: 信道编码为(二进制)信息序列引入剩余度, 以提高信息传输的可靠性, 输出二进制数字序列
• 脉冲调制: 又称为基带调制, 由数字脉冲调试器实现
  • 数字脉冲调制器: 将数字序列映射为适合基带信道传输的脉冲波形的数字调制器, 输出数字基带信号
    • 数字基带信号: 信号波形的功率谱为低通型, 只有直流或低频成分, 带宽有限的数字信号
  • 数字调制器有二进制与M进制两种
    • 二进制数字调制器: 将二进制数字序列中的二进制符号0映射为信号波形 $s_1(t)$, 将二进制符号1映射为信号波形 $s_2(t)$
    • M进制数字调制器: 将二进制数字序列中的K个二进制符号映射为 $M=2^K$ 个不同信号的波形 $s_i(t),i=1,2,\cdots M$
• 带通调制: 将基带信号进行上变频, 搬移到载频上成为频带信号, 输入基带波形, 输出频带波形
  • 数字基带传输系统没有该模块
• 信道: 数字信号的信道分为基带信道(低通信道)与带通信道
  • 基带信道: 传递函数为低通型, 适合传送脉冲信号, 例如同轴电缆与双绞线
  • 带通信道: 传递函数为带通型, 适合传送带通信号, 例如无线通信与光通信
• 带通解调: 将频带信号进行下变频, 搬移到基频上成为基带信号, 输入频带波形, 输出基带波形
  • 数字基带传输系统没有该模块
• 检测: 将基带信号波形中的二进制数字序列提取出来
  • 由于噪声干扰的影响，其输出的二进制数字序列与原始二进制数字序列不完全相同, 即出现传输错误
• 信道译码: 去掉二进制数字序列中的冗余比特, 实现检错或者纠错功能
• 信源译码: 恢复原始消息

根据是否进行带通调制与带通解调可将数字传输系统分为数字基带传输系统与数字频带传输系统

• 数字基带传输系统: 将数字基带信号通过基带信道传输的系统, 不进行带通调制与带通解调
• 数字频带传输系统: 将数字基带信号通过频带调制器进行带通调制, 搬移到载频上成为带通信号, 通过带通信道传输, 再通过频带解调器进行带通解调, 恢复成数字基带信号的传输系统

1.1.2 数字基带传输系统

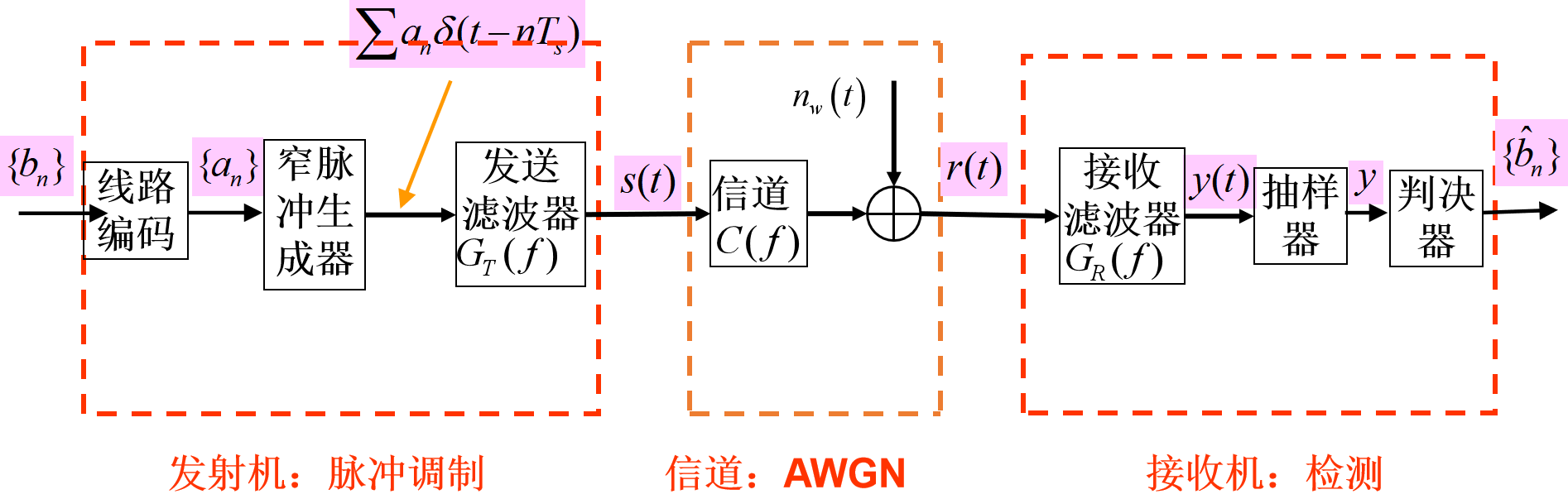
发射机(脉冲调制)

将自信源的二进制随机序列 { b n } \{b_n\} { bn​} 变为信号波形 $s(t)$

线路编码

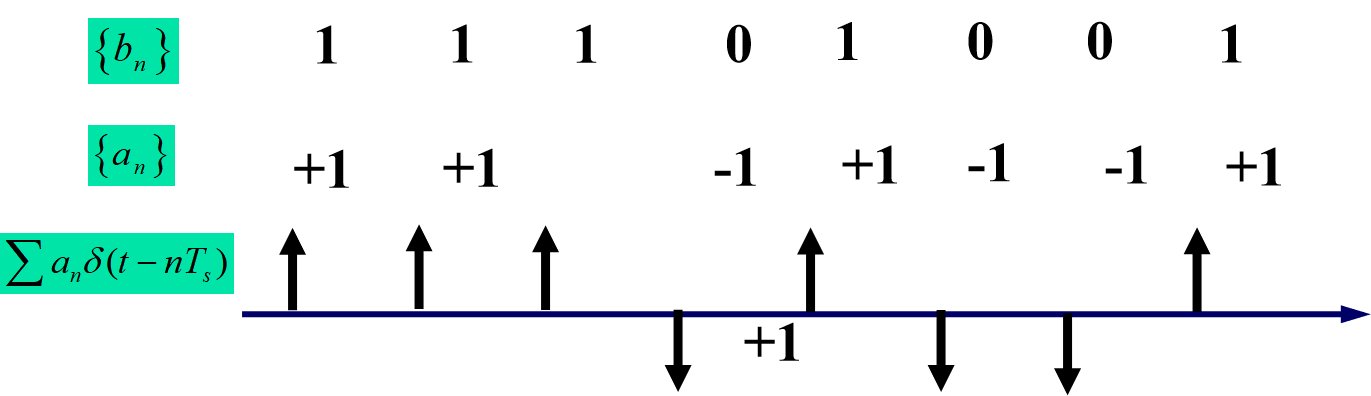
将二进制随机序列 { b n } \{b_n\} { bn​} 映射为电平 { a n } \{a_n\} { an​}

• 单极性码: 将“0”映射为零电平, “1”映射为正电平
• 双极性码: 将“0”映射为负电平, “1”映射为正电平

窄脉冲生成器

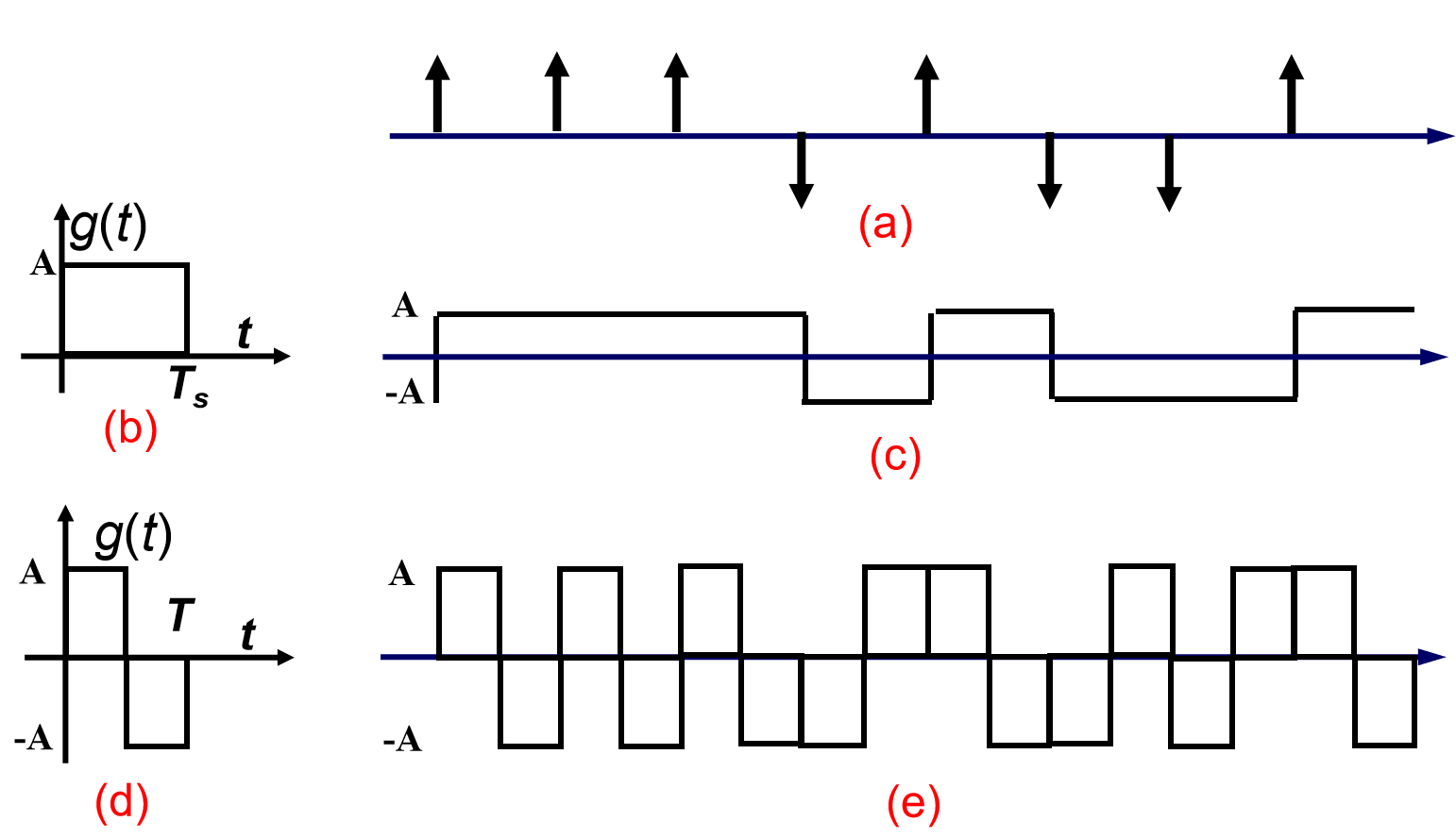
产生间隔为 $T_s$ 的冲激序列, 如 图1.1.2.2

• 输入: 电平 { a n } \{a_n\} { an​}
• 输出: 冲激序列
  $$m(t)=\sum _{n=-\infty }^{\infty }{a}_n\delta (t-n{T}_s)\text{\hspace{1em}(1.1.2.1)}$$
  • 码元间隔: $T_s$, 每个码元所对应的传输时间
  • 码元传输速率: $r_s=\frac{1}{T_s}$, 单位时间内传输码元数量

发送滤波器

产生信号发送波形 $s(t)$

• 输入: 冲激序列 $m(t)$
• 输出: 信号波形
  $$s(t)=\sum _{n=-\infty }^{\infty }{a}_n{g}_T(t-n{T}_s)\text{\hspace{1em}(1.1.2.2)}$$
  • 发送滤波器的冲激响应: $g_T(t)$
  • 发送滤波器的系统响应函数: $G_T(f)$

信道(AWGN信道)

发射机产生的发送信号经过信道进入接收机

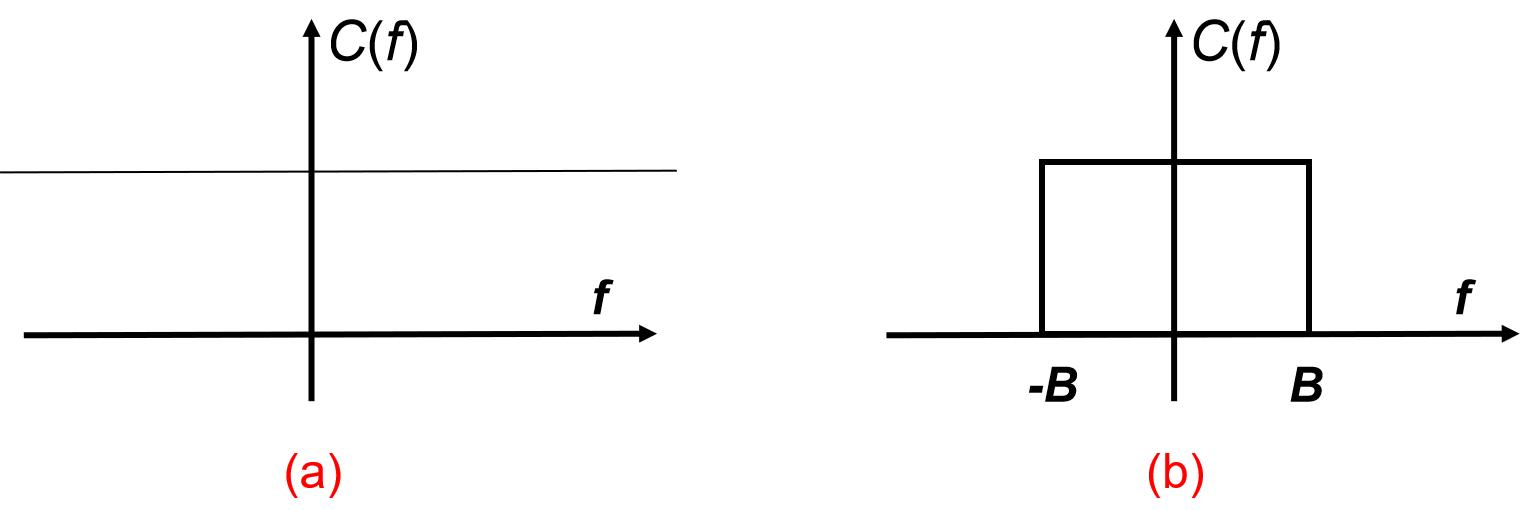
• 带宽无限AWGN信道: 信道的频率传递函数 $C(f)$ 在整个频率上是常数, 发送信号 $s(t)$ 通过 $C(f)$ 过程中时域波形不会发生形状上的变化, 接收信号为
  $$r(t)=s(t)+n_w(t)\text{\hspace{1em}(1.1.2.3)}$$
• 带宽有限AWGN信道: 信道的频率传递函数 $C(f)$ 近似于理想低通滤波器的系统函数, 发送信号 $s(t)$ 通过 $C(f)$ 过程中信号的高频成分将被滤掉, 接收信号为
  $$r(t)=s(t)\ast c(t)+n_w(t)\text{\hspace{1em}(1.1.2.4)}$$

接收机(检测)

将来自信道的接收波形 $r(t)$ 恢复成二进制序列 { b n ^ } \{\hat{b_n}\} { bn​^​}, 理想情况下 { b n ^ } \{\hat{b_n}\} { bn​^​} 与 { b n } \{b_n\} { bn​} 应完全相同, 实际传输过程中由于噪声等影响, 会发生误码

接收滤波器

为使抽样器在最佳采样时刻 $t_0$ 的信噪比最大, 进而使判决器使用合适的判决门限 $V_T$ 进行判决后平均误比特率最小(最佳接收), 需要使用匹配滤波器(MF)或相关接收机

• 匹配滤波器: 在最佳采样时刻 $t=t_0$ 使滤波器的输出信号 $y_{MF}(t)$ 的瞬时功率与输出噪声的平均功率之比(输出信噪比)最大的线性滤波器
  $$\begin{array}{rl}y(t)& =r(t)\ast h_{MF}(t)\\ & =(s_i(t)+n_w(t))\ast h_{MF}(t)\\ & =s_o(t)+n_o(t)\end{array}\text{\hspace{1em}(1.1.2.5)}$$
  • 物理可实现的匹配滤波器
    $$h_{MF}(t)=K\cdot s_i(T_s-t)\text{\hspace{1em}(1.1.2.6)}$$
• 相关接收机: 对接收信号的与其自己的乘积进行积分, 输出信号 $y_{CR}(t)$ 满足 $y_{CR}(t_0)=y_{MF}(t_0)$
  $$\begin{array}{rl}y(t)& =s(t)\ast h(t)\\ & ={\int }_{-\infty }^{\infty }h(\alpha )\cdot s(t-\alpha )\\ & ={\int }_0^{T}K\cdot s(T_s-\alpha )\cdot s(t-\alpha )\\ & =K\cdot R_s(t-T_s)\end{array}\text{\hspace{1em}(1.1.2.7)}$$

抽样器

在接收滤波器输出信号的输出信噪比最大的时刻(最佳采样时刻) $t=t_0$ 对接收滤波器的输出信号进行采样
$$y=y(t_0)\text{\hspace{1em}(1.1.2.8)}$$

判决器

对抽样器经过抽样获得的序列 { y } \{y\} { y} 与判决门限 $V_T$ 进行比较, 根据比较结果输出 $\hat{b}=1$ 或 $\hat{b}=0$, 形成输出比特序列 { b ^ } \{\hat{b}\} { b^}

1.1.3 数字频带传输系统

将数字基带信号通过频带调制器进行带通调制, 搬移到载频上成为带通信号, 通过带通信道传输, 再通过频带解调器进行带通解调, 恢复成数字基带信号的传输系统即为数字频带传输系统.

信道(带限AWGN信道)

• 带通有限AWGN信道: 信道的频率传递函数 $C(f)$ 近似于理想带通滤波器的系统函数, 发送信号 $s(t)$ 通过 $C(f)$ 过程中信号的阻带成分将被滤掉, 接收信号为
  $$r(t)=s(t)\ast c(t)+n_w(t)\text{\hspace{1em}(1.1.3.1)}$$

1.2 研究问题

针对信道带宽无限的单极性基带基带传输系统与信号带宽受限的双极性基带传输系统, 采用匹配滤波器(相关接收机), 对误码性能进行仿真:

• 选择系统模型, 对系统模型进行分析, 推导误码率理论结果
• 选择仿真工具, 搭建仿真模型, 设置仿真参数进行仿真, 获得误码率仿真结果
• 将仿真结果与误码率结果进行比较, 进行误差分析, 得出结论

2. 系统模型

传输系统为数字基带传输系统时, 其基本模型如下图所示

2.1 信号带宽无限时的单极性基带传输系统模型

带宽无限的理想AWGN信道的传输函数 $C(f)$ 的幅频特性曲线如 图1.1.2.3 (a) 所示, 为一个恒定的值.
为保证通过接收滤波器后

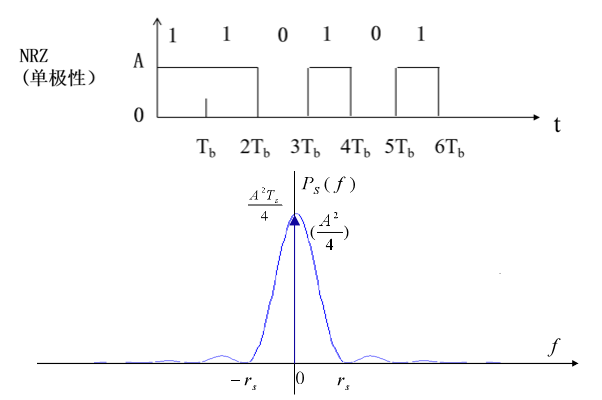
2.1.1 不归零码(NRZ)

单极性不归零码幅度序列 { a n } \{a_n\} { an​} 为:
$$a_n=\{\begin{array}{ll}A,& i=1\\ 0,& i=2\end{array}\text{\hspace{1em}(2.1.1.1)}$$

单极性不归零码冲激序列表达式:
$$\sum _{n=-\infty }^{\infty }{a}_n\delta (t-n{T}_s)\text{\hspace{1em}(2.1.1.2)}$$

单极性不归零码发送信号 $s(t)$ 表达式:
$$s(t)=\sum _{n=-\infty }^{\infty }{a}_n{g}_T(t-n{T}_s)\text{\hspace{1em}(2.1.1.3)}$$

其中, 发送滤波器单位脉冲响应 $g_T(t)$:
$$g_T(t)=A\cdot Rect(\frac{t}{T_s})=\{\begin{array}{ll}A,& 0<t<T_s\\ 0,& 其它\end{array}\text{\hspace{1em}(2.1.1.4)}$$

系统函数 $G_T(f)$:
$$G_T(f)=A{T}_{s}Sa(\pi f{T}_s)\text{\hspace{1em}(2.1.1.5)}$$

发送信号功率谱密度表达式(0, 1等概):
$$\begin{array}{rl}{P}_s(f)& =\frac{{\sigma }_a^2}{T_s}|G_T(f){|}^2+\frac{m_a^2}{T_s^2}\sum _{k=-\infty }^{\infty }|G_T(\frac{k}{T_s}){|}^2\delta (f-\frac{k}{T_s})\\ & =\frac{A^2{T}_s}{4}S{a}^2(\pi f{T}_s)+\frac{A^2}{4}\delta (f)\end{array}\text{\hspace{1em}(2.1.1.6)}$$

接收滤波器输入信号:
$$r(t)=s_i(t)+n_w(t)\text{\hspace{1em}(2.1.1.7)}$$

其中
$$s_i(t)=\{\begin{array}{ll}{s}_1(t)=A,& 发送"1"\\ s_2(t)=0,& 发送"0"\end{array}\text{\hspace{1em}(2.1.1.8)}$$

匹配滤波器/相关接收机输出信号(传输 $s_1(t)$ 时):
$$\begin{array}{rl}y(t)& =r(t)\ast h(t)\\ & ={\int }_0^{t}r(\tau )h(t-\tau )d\tau \\ & ={\int }_0^{t}r(\tau )s_1(T-t+\tau )d\tau \\ & ={\int }_0^t[s_1(\tau )+n_w(\tau )]s_1(T-t+\tau )d\tau \end{array}\text{\hspace{1em}(2.1.1.9)}$$

其中, 匹配滤波器的单位冲激响应 $h(t)$:
$$h(t)=s_1(T-t)\text{\hspace{1em}(2.1.1.10)}$$

在最佳抽样时刻($T=T_s$)进行抽样(传输 $s_1(t)$ 时), 得:
$$\begin{array}{rl}{y}_1& \equiv y(T)\\ & ={\int }_0^T[s_1(\tau )+n_w(\tau )]s_1(\tau )d\tau \\ & ={\int }_0^T{s}_1^2(\tau )d\tau +{\int }_0^T{s}_1(\tau )n_w(\tau )d\tau \\ & =E_{s1}+Z\end{array}\text{\hspace{1em}(2.1.1.11)}$$

同理可得传输信号 $s_2(t)$ 时有:
$$\begin{array}{rl}{y}_2& \equiv y(T)\\ & ={\int }_0^T[s_2(\tau )+n_w(\tau )]s_1(\tau )d\tau \\ & ={\int }_0^T{s}_1(\tau )s_2(\tau )d\tau +{\int }_0^T{s}_1(\tau )n_w(\tau )d\tau \\ & =0+Z\end{array}\text{\hspace{1em}(2.1.1.12)}$$

其中 $E_{s1}$ 为传输符号 $s_1$ 时有用信号的能量, $Z$ 为传输符号 $s_1$ 时噪声的能量
$$E_{s1}={\int }_0^{T_s}{s}_1^2(\tau )d\tau =A^2{T}_s\text{\hspace{1em}(2.1.1.13)}$$
$$Z={\int }_0^{T_s}{s}_1(\tau )n_w(\tau )d\tau \text{\hspace{1em}(2.1.1.14)}$$
$$E(Z|s_1)=0\text{\hspace{1em}(2.1.1.15)}$$
$$\begin{array}{rl}D(Z|s_1)& ={\sigma }^2\\ & =E\{[Z-E(Z){]}^2|s_1\}\\ & =E[{\int }_0^{T_s}{\int }_0^{T_s}{n}_w(t_1)n_w(t_2)s_1(t_1)s_1(t_2)d{t}_{1}d{t}_2]\\ & ={\int }_0^{T_s}{\int }_0^{T_s}E[n_w(t_1)n_w(t_2)]s_1(t_1)s_1(t_2)d{t}_{1}d{t}_2\\ & ={\int }_0^{T_s}{\int }_0^{T_s}{R}_w(\tau )s_1(t_1)s_1(t_2)d{t}_{1}d{t}_2\\ & ={\int }_0^{T_s}{\int }_0^{T_s}\frac{N_0}{2}\delta (\tau )s_1(t_1)s_1(t_2)d{t}_{1}d{t}_2\\ & =\frac{N_0}{2}{E}_{s1}\end{array}\text{\hspace{1em}(2.1.1.16)}$$

• 其中 $\tau =t_2-t_1$

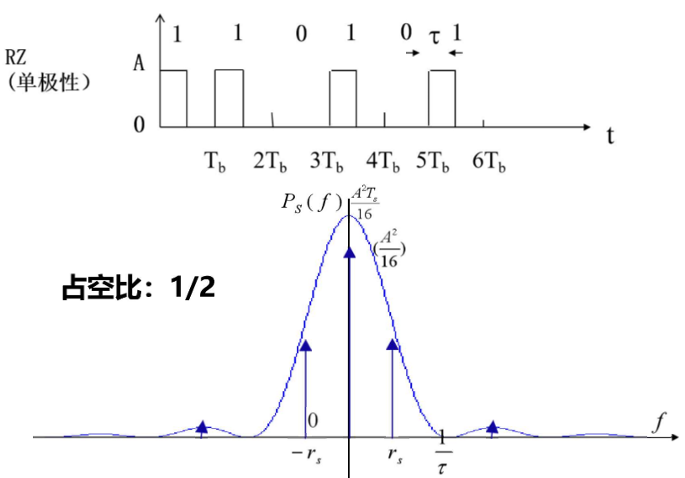
2.1.2 归零码(RZ, 50%)

单极性归零码幅度序列 { a n } \{a_n\} { an​} 同公式 (2.1.1.1):
$$a_n=\{\begin{array}{ll}A,& i=1\\ 0,& i=2\end{array}\text{\hspace{1em}(2.1.2.1)}$$

单极性归零码冲激序列表达式同公式 (2.1.1.2):
$$\sum _{n=-\infty }^{\infty }{a}_n\delta (t-n{T}_s)\text{\hspace{1em}(2.1.2.2)}$$

单极性归零码发送信号 $s(t)$ 表达式同公式 (2.1.1.3):
$$s(t)=\sum _{n=-\infty }^{\infty }{a}_n{g}_T(t-n{T}_s)\text{\hspace{1em}(2.1.2.3)}$$

其中, 发送滤波器单位脉冲响应 $g_T(t)$:
$$g_T(t)=A\cdot Rect(\frac{2t}{T_s})=\{\begin{array}{ll}A,& 0<t<\frac{T_s}{2}\\ 0,& 其它\end{array}\text{\hspace{1em}(2.1.2.4)}$$

系统函数 $G_T(f)$:
$$G_T(f)=\frac{A{T}_s}{2}Sa(\frac{\pi f{T}_s}{2})\text{\hspace{1em}(2.1.2.5)}$$

发送信号功率谱密度表达式(0, 1等概):
$$\begin{array}{rl}{P}_s(f)& =\frac{{\sigma }_a^2}{T_s}|G_T(f){|}^2+\frac{m_a^2}{T_s^2}\sum _{k=-\infty }^{\infty }|G_T(\frac{k}{T_s}){|}^2\delta (f-\frac{k}{T_s})\\ & =\frac{A^2{T}_s}{16}S{a}^2(\frac{\pi f{T}_s}{2})+\frac{A^2}{16}\sum _{k=-\infty }^{\infty }{Sa}^2(\frac{k\pi }{2})\delta (f-\frac{k}{T_s})\end{array}\text{\hspace{1em}(2.1.2.6)}$$

接收滤波器输入信号, 同公式 (2.1.1.7):
$$r(t)=s_i(t)+n_w(t)\text{\hspace{1em}(2.1.2.7)}$$

其中
$$s_i(t)=\{\begin{array}{ll}{s}_1(t)=A,& 发送"1",0<t<\frac{T_s}{2}\\ s_1(t)=0,& 发送"1",\frac{T_s}{2}<t<T_s\\ s_2(t)=0,& 发送"0"\end{array}\text{\hspace{1em}(2.1.2.8)}$$

匹配滤波器/相关接收机输出信号(传输 $s_1(t)$ 时), 同公式 (2.1.1.9):
$$\begin{array}{rl}y(t)& =r(t)\ast h(t)\\ & ={\int }_0^{t}r(\tau )h(t-\tau )d\tau \\ & ={\int }_0^{t}r(\tau )s_1(T-t+\tau )d\tau \\ & ={\int }_0^t[s_1(\tau )+n_w(\tau )]s_1(T-t+\tau )d\tau \end{array}\text{\hspace{1em}(2.1.2.9)}$$

其中, 匹配滤波器的单位冲激响应 $h(t)$, 同公式 (2.1.1.10):
$$h(t)=s_1(T-t)\text{\hspace{1em}(2.1.2.10)}$$

在最佳抽样时刻($T=\frac{T_s}{2}$)进行抽样(传输 $s_1(t)$ 时), 同公式(2.1.2.11):
$$\begin{array}{rl}{y}_1& \equiv y(T)\\ & ={\int }_0^T[s_1(\tau )+n_w(\tau )]s_1(\tau )d\tau \\ & ={\int }_0^T{s}_1^2(\tau )d\tau +{\int }_0^T{s}_1(\tau )n_w(\tau )d\tau \\ & =E_{s1}+Z\end{array}\text{\hspace{1em}(2.1.2.11)}$$

同理可得传输信号 $s_2(t)$ 时同公式 (2.1.2.12):
$$\begin{array}{rl}{y}_2& \equiv y(T)\\ & ={\int }_0^T[s_2(\tau )+n_w(\tau )]s_1(\tau )d\tau \\ & ={\int }_0^T{s}_1(\tau )s_2(\tau )d\tau +{\int }_0^T{s}_1(\tau )n_w(\tau )d\tau \\ & =0+Z\end{array}\text{\hspace{1em}(2.1.2.12)}$$

其中 $E_{s1}$ 为传输符号 $s_1$ 时有用信号的能量, $Z$ 为传输符号 $s_1$ 时噪声的能量
$$E_{s1}={\int }_0^{\frac{T_s}{2}}{s}_1^2(\tau )d\tau =A^2\frac{T_s}{2}\text{\hspace{1em}(2.1.2.13)}$$
$$Z={\int }_0^{\frac{T_s}{2}}{s}_1(\tau )n_w(\tau )d\tau \text{\hspace{1em}(2.1.2.14)}$$
$$E(Z|s_1)=0\text{\hspace{1em}(2.1.2.15)}$$
$$\begin{array}{rl}D(Z|s_1)& ={\sigma }^2\\ & =E\{[Z-E(Z){]}^2|s_1\}\\ & =E[{\int }_0^{\frac{T_s}{2}}{\int }_0^{\frac{T_s}{2}}{n}_w(t_1)n_w(t_2)s_1(t_1)s_1(t_2)d{t}_{1}d{t}_2]\\ & ={\int }_0^{\frac{T_s}{2}}{\int }_0^{\frac{T_s}{2}}E[n_w(t_1)n_w(t_2)]s_1(t_1)s_1(t_2)d{t}_{1}d{t}_2\\ & ={\int }_0^{\frac{T_s}{2}}{\int }_0^{\frac{T_s}{2}}{R}_w(\tau )s_1(t_1)s_1(t_2)d{t}_{1}d{t}_2\\ & ={\int }_0^{\frac{T_s}{2}}{\int }_0^{\frac{T_s}{2}}\frac{N_0}{2}\delta (\tau )s_1(t_1)s_1(t_2)d{t}_{1}d{t}_2\\ & =\frac{N_0}{2}{E}_{s1}\end{array}\text{\hspace{1em}(2.1.2.16)}$$

• 其中 $\tau =t_2-t_1$

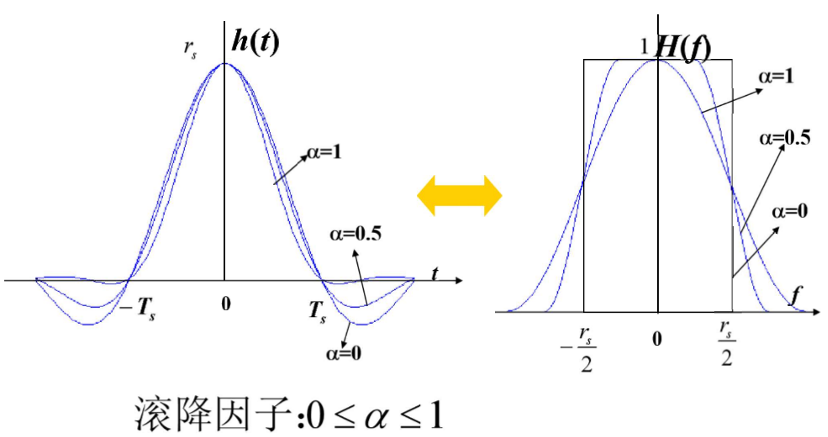
2.1.3 升余弦传输(RC)

升余弦传输系统冲激序列表达式同公式 (2.1.1.2):
$$\sum _{n=-\infty }^{\infty }{a}_n\delta (t-n{T}_s)\text{\hspace{1em}(2.1.3.2)}$$

升余弦传输系统发送信号 $s(t)$ 表达式:
$$s(t)=\sum _{n=-\infty }^{\infty }{a}_n{h}_{RRC}(t-n{T}_s)\text{\hspace{1em}(2.1.3.3)}$$

其中, 由发送滤波器(根升余弦滤波器), 带宽无限信号与接收滤波器(根升余弦滤波器)组成的升余弦基带成型网络的单位脉冲响 $h_{RC}(t)$ 与系统函数 $H_{RC}(f)$ 如 图2.1.3.1 所示.
升余弦单位脉冲响应表达式 $h_{RC}(t)$:
$$h_{RC}(t)=sa(\frac{\pi t}{T_s})\frac{cos(\frac{\alpha \pi t}{T_s})}{1-\frac{4{\alpha }^2{t}^2}{T_s^2}}\text{\hspace{1em}(2.1.3.</}$$