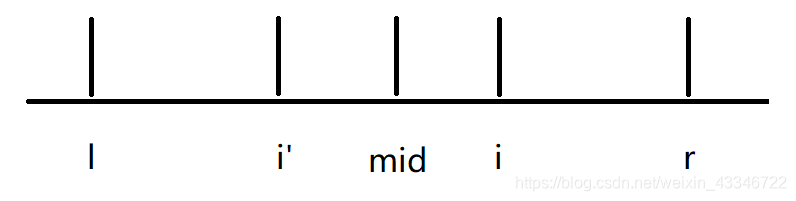Palindrome \operatorname{Palindrome} Palindrome
题目链接: POJ 3974 \operatorname{POJ\ 3974} POJ 3974
题目大意
就是给你很多个字符串,让你求字符串的最大回文子串长度。
题目
Andy the smart computer science student was attending an algorithms class when the professor asked the students a simple question, “Can you propose an efficient algorithm to find the length of the largest palindrome in a string?”
A string is said to be a palindrome if it reads the same both forwards and backwards, for example “madam” is a palindrome while “acm” is not.
The students recognized that this is a classical problem but couldn’t come up with a solution better than iterating over all substrings and checking whether they are palindrome or not, obviously this algorithm is not efficient at all, after a while Andy raised his hand and said “Okay, I’ve a better algorithm” and before he starts to explain his idea he stopped for a moment and then said “Well, I’ve an even better algorithm!”.
If you think you know Andy’s final solution then prove it! Given a string of at most 1000000 characters find and print the length of the largest palindrome inside this string.
输入
Your program will be tested on at most 30 test cases, each test case is given as a string of at most 1000000 lowercase characters on a line by itself. The input is terminated by a line that starts with the string “END” (quotes for clarity).
输出
For each test case in the input print the test case number and the length of the largest palindrome.
样例输入
abcbabcbabcba
abacacbaaaab
END
样例输出
Case 1: 13
Case 2: 6
数据范围
数据的组数不会超过 30 30 30 组,字符的长度最多是由 1000000 1000000 1000000 个字符组成。
思路
这道题是一道求最长回文子串长度的模板题。
我这里就不用二分加 hash 的 n l o g n nlogn nlogn 做法,直接学了 O ( n ) O(n) O(n) 的 Manacher 算法来用。
因为回文串长度为单数的和双数的要分开讨论,我们就直接处理字符串,让它只剩单数的情况。
我们在每个字符之间加一个莫得的字符,我用了
#
\#
# 这个。
我们举个栗子,一个字符串
a
f
d
a
e
afdae
afdae 在处理之后就变成了
#
a
#
f
#
d
#
a
#
e
#
\#a\#f\#d\#a\#e\#
#a#f#d#a#e# 。
那如果是
n
2
n^2
n2 暴力,我们就是枚举每个位置作为回文串的中心,然后暴力求出最大的长度。
那我们 Manacher 算法就是从这个地方开始优化。
第一步:预处理
我们让
r
r
r 为直接枚举中间点所有的最右回文边界再右一位,
m
i
d
mid
mid 则为这个
r
r
r 是以哪个中间点得出的字符串右边界再右一位。
这两个值都预处理成
−
1
-1
−1 。
而且还要用一个数组来记录以这个点为中心点的最大回文串半径
+
1
+1
+1 是多少。(我用
b
j
[
i
]
bj[i]
bj[i] 来存)
第二部:开始遍历每一个点,分类讨论
1.
i
>
r
i>r
i>r ,就只能暴力从
1
1
1 开始匹配。
2.
i
<
=
r
i<=r
i<=r ,就可以加速处理出来,但是又要分情况,我们先弄一个图:
(
i
i
i 对于
m
i
d
mid
mid 的对称点是
i
′
i'
i′ ,
l
l
l 对于
m
i
d
mid
mid 的对称点是
l
l
l )
(可以看出
i
−
m
i
d
=
m
i
d
−
i
′
i-mid=mid-i'
i−mid=mid−i′ ,从而得出
i
′
=
m
i
d
∗
2
−
i
i'=mid*2-i
i′=mid∗2−i )
-
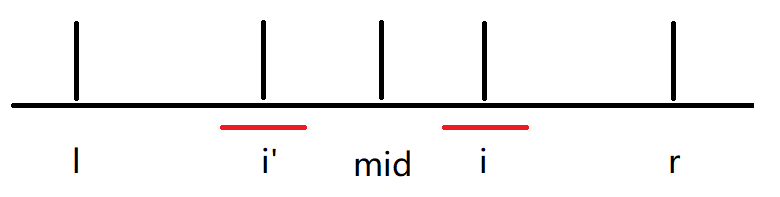
i ′ i' i′ 的最大回文在 l r lr lr 里面,那其实 i i i 的最大回文长度就是 i ′ i' i′ 的。
-
i ′ i' i′ 的最大回文超过了 l r lr lr ,那 i i i 的最大回文长度是 r − i r-i r−i。
为什么呢?
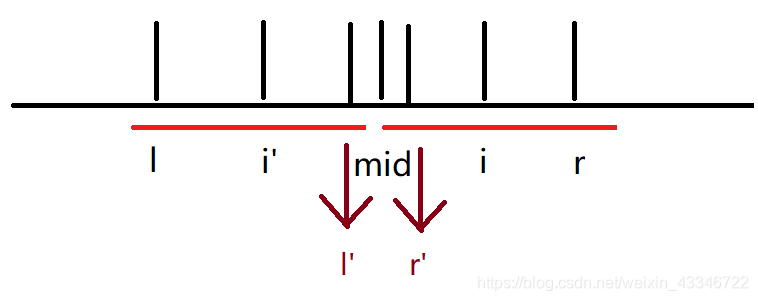
我们让 l ′ l' l′ 是 l l l 对于 i ′ i' i′ 的对称点, r ′ r' r′ 是 r − 1 r-1 r−1 对于 i i i 的对称点, a [ i ] a[i] a[i] 就是字符串第 i i i 为是什么字符。
我们可以知道, a [ l ] = a [ l ′ ] a[l]=a[l'] a[l]=a[l′] ,那因为 m i d mid mid 为中心的对称,我们就知道 a [ r − 1 ] = a [ r ′ ] a[r-1]=a[r'] a[r−1]=a[r′] 。那回文半径就至少有 r − i − 1 r-i-1 r−i−1 。
那我们还可以知道 a [ l − 1 ] = a [ l ′ + 1 ] a[l-1]=a[l'+1] a[l−1]=a[l′+1] ,而且通过 m i d mid mid 为中心的对称,我们又知道 a [ l ′ + 1 ] = a [ r ′ − 1 ] a[l'+1]=a[r' - 1] a[l′+1]=a[r′−1] , a [ l − 1 ] ! = a [ r ] a[l-1]!=a[r] a[l−1]!=a[r] (因为如果相等那 m i d mid mid 的最大回文半径就还可以 + 1 +1 +1 )。
那等量代换一下,就得到了 a [ r ′ − 1 ] ! = a [ r ] a[r'-1]!=a[r] a[r′−1]!=a[r] ,那最大回文半径就是 r − i − 1 r-i-1 r−i−1 了。 -
i ′ i' i′ 的最大回文刚好在 l r lr lr 那,那就对于 i i i 的长度直接从 i ′ i' i′ 的最大长度开始暴力,这里就不画图了。
那我们就选这三种中最大的那一种。
这时候有人就会问了:你只是求出来新字符串的最长子回文串的半径,但是题目要的是原来字符串的最长回文子串长度啊!
那我们就发现,其实原来字符串的最长回文子串长度就是新字符串的最长子回文串的半径
−
1
-1
−1 。
为什么呢?
- 原来字符串的最长回文子串长度是奇数:
我们假设一个新字符串的最长子回文串是 # a # b # c # b # a # \#a\#b\#c\#b\#a\# #a#b#c#b#a# ,那新字符串的最长子回文串的半径就是 6 6 6 。
这个时候我们再看:这个新字符串的最长回文子串的左边一半是 # a # b # c \#a\#b\#c #a#b#c ,那包含了多少个原来字符串的字符呢?可以发现这个子串的分布规律是一个 # \# # 一个原字符串的字符这样的排列,那就包含了 a n s / 2 ans/2 ans/2 个原来字符串的字符。
(我们设 a n s ans ans 为新字符串的最长子回文串的半径)
接着,因为我们可以知道原来字符串的最长回文子串长度是奇数,那它的一半 ∗ 2 − 1 *2-1 ∗2−1 就是它。
那原来字符串的最长回文子串长度就是 a n s / 2 ∗ 2 − 1 = a n s − 1 ans/2*2-1=ans-1 ans/2∗2−1=ans−1 - 原来字符串的最长回文子串长度是偶数:
我们假设一个新字符串的最长子回文串是 # a # b # c # c # b # a # \#a\#b\#c\#c\#b\#a\# #a#b#c#c#b#a# ,那新字符串的最长子回文串的半径就是 7 7 7 。
这个时候我们再看:这个新字符串的最长回文子串的左边一半是 # a # b # c # \#a\#b\#c\# #a#b#c# ,那包含了多少个原来字符串的字符呢?可以发现这个子串的分布规律是一个 # \# # 一个原字符串的字符这样的排列,最后再多一个 # \# #,那就包含了 ( a n s − 1 ) / 2 (ans-1)/2 (ans−1)/2 个原来字符串的字符。(这里的 / / / 不是整除)
( a n s ans ans 跟上面一样)
接着,因为我们可以知道原来字符串的最长回文子串长度是偶数,那它的一半 ∗ 2 *2 ∗2 就是它。
那原来字符串的最长回文子串长度就是 ( a n s − 1 ) / 2 ∗ 2 = a n s − 1 (ans-1)/2*2=ans-1 (ans−1)/2∗2=ans−1
那这样,我们就做到了 O ( n ) O(n) O(n) 。
代码
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int tmp, n, nn, bj[3000001];
int r, mid, ans;
char a[3000001], b[6000002];
int getans() {
n = strlen(a);//原字符串的长度
nn = n * 2 + 1;//新字符串的长度
for (int i = 0; i < nn; i++)
b[i] = (i & 1) ? a[i / 2] : '#';//弄出新字符串
r = -1;//初始化
mid = -1;
ans = 0;
for (int i = 0; i < nn; i++) {
bj[i] = (i > r) ? 1 : min(bj[2 * mid - i], r - i);//i关于mid的对称点在r的里面还是外面
while (i - bj[i] >= 0 && i + bj[i] < nn && b[i - bj[i]] == b[i + bj[i]])//暴力往外找
bj[i]++;
if (i + bj[i] > r) {//此回文串的右节点更右
r = i + bj[i];//更新
mid = i;
}
ans = max(ans, bj[i]);//取最大值
}
return ans - 1;//原字符串的长度就是新字符串的长度-1
}
int main() {
scanf("%s", &a);//读入
while (!(strlen(a) == 3 && a[0] == 'E' && a[1] == 'N' && a[2] == 'D')) {
printf("Case %d: %d\n", ++tmp, getans());//Manacher算法
scanf("%s", &a);//读入
}
return 0;
}