【MindSpore学习打卡】应用实践-自然语言处理-深入理解LSTM+CRF在序列标注中的应用

在自然语言处理(NLP)领域，序列标注是一项重要的任务。其目标是为给定的输入序列中的每个Token分配一个标签。序列标注的应用范围广泛，包括分词、词性标注、命名实体识别(NER)等。在本文中，我们将探讨如何利用LSTM和CRF模型进行序列标注，并使用MindSpore框架实现这一过程。通过深入了解LSTM和CRF的原理和实现方法，读者将能够更好地理解和应用这些技术来解决实际问题。

条件随机场(Conditional Random Field, CRF)

在序列标注任务中，简单地将每个Token的标签预测视为多分类问题是不够的，因为相邻Token之间存在依赖关系。以命名实体识别为例：

输入序列	清	华	大	学	座	落	于	首	都	北	京
输出标注	B	I	I	I	O	O	O	O	O	B	I

在上述例子中，清华大学和北京是地名，需要将其识别出来。我们对每个输入的单词预测其标签，最后根据标签来识别实体。为了捕获这种依赖关系，我们引入条件随机场(CRF)。

为什么需要CRF

在序列标注任务中，简单地将每个Token的标签预测视为多分类问题是不够的，因为相邻Token之间存在依赖关系。比如在命名实体识别任务中，一个实体的开始标签通常是"B"，后续的标签是"I"，而非实体的标签是"O"。如果我们不考虑这种依赖关系，模型可能会产生不合理的标签序列。条件随机场(CRF)通过引入发射概率和转移概率，能够捕获这种标签间的依赖关系，从而提高预测的准确性。

CRF的定义与参数化形式

CRF是一种概率图模型，适用于捕获序列中相邻Token之间的依赖关系。设 $x=\{x_0, ..., x_n\}$ 为输入序列， $y=\{y_0, ..., y_n\}$ 为输出的标注序列，其中 $n$ 为序列的最大长度。则输出序列 $y$ 的概率为：

$\frac{\exp{(\text{Score}(x, y)})}{\sum_{y' \in Y} \exp{(\text{Score}(x, y')})}$

其中， $\text{Score}(x, y)$ 用于衡量序列 $x$ 和标签 $y$ 的匹配程度。我们定义两个概率函数来计算 $\text{Score}$ ：

发射概率函数 $\psi_\text{EMIT}$ ：表示 $x_i \rightarrow y_i$ 的概率。
转移概率函数 $\psi_\text{TRANS}$ ：表示 $y_{i-1} \rightarrow y_i$ 的概率。

基于这两个函数，我们可以得到 $\text{Score}$ 的计算公式：

$\text{Score}(x,y) = \sum_i \log \psi_\text{EMIT}(x_i \rightarrow y_i) + \log \psi_\text{TRANS}(y_{i-1} \rightarrow y_i)$

CRF的实现

在实现CRF时，我们需要计算正确标签序列的得分(Score)和所有可能标签序列的对数指数和(Normalizer)。然后通过求解负对数似然损失(NLL)来进行模型训练。

Score计算

为什么需要序列填充和掩码

在实际应用中，输入序列的长度可能不一致。为了将这些序列打包成一个Batch，我们需要对长度不足的序列进行填充。然而，填充的部分不应参与模型的训练和预测。因此，我们引入了掩码矩阵(mask)，用于忽略填充部分的计算。这样可以确保模型只关注有效的Token，提高训练和预测的准确性。

首先根据公式计算正确标签序列的得分：

def compute_score(emissions, tags, seq_ends, mask, trans, start_trans, end_trans):
    seq_length, batch_size = tags.shape
    mask = mask.astype(emissions.dtype)

    score = start_trans[tags[0]]
    score += emissions[0, mnp.arange(batch_size), tags[0]]

    for i in range(1, seq_length):
        score += trans[tags[i - 1], tags[i]] * mask[i]
        score += emissions[i, mnp.arange(batch_size), tags[i]] * mask[i]

    last_tags = tags[seq_ends, mnp.arange(batch_size)]
    score += end_trans[last_tags]

    return score

Normalizer计算

接下来，我们使用动态规划算法计算Normalizer：

def compute_normalizer(emissions, mask, trans, start_trans, end_trans):
    seq_length = emissions.shape[0]

    score = start_trans + emissions[0]

    for i in range(1, seq_length):
        broadcast_score = score.expand_dims(2)
        broadcast_emissions = emissions[i].expand_dims(1)
        next_score = broadcast_score + trans + broadcast_emissions
        next_score = ops.logsumexp(next_score, axis=1)
        score = mnp.where(mask[i].expand_dims(1), next_score, score)

    score += end_trans
    return ops.logsumexp(score, axis=1)

Viterbi算法

为什么使用Viterbi算法

在解码阶段，我们需要找到使得序列得分最高的标签序列。穷举所有可能的标签序列并计算其得分是不可行的，因为可能的标签序列数量是指数级的。Viterbi算法是一种动态规划算法，能够高效地找到最优标签序列。它通过逐步计算每个Token对应的最优标签，并保存中间结果，避免了重复计算，从而大大提高了解码的效率。

在解码阶段，我们使用Viterbi算法求解最优标签序列：

def viterbi_decode(emissions, mask, trans, start_trans, end_trans):
    seq_length = mask.shape[0]

    score = start_trans + emissions[0]
    history = ()

    for i in range(1, seq_length):
        broadcast_score = score.expand_dims(2)
        broadcast_emission = emissions[i].expand_dims(1)
        next_score = broadcast_score + trans + broadcast_emission
        indices = next_score.argmax(axis=1)
        history += (indices,)
        next_score = next_score.max(axis=1)
        score = mnp.where(mask[i].expand_dims(1), next_score, score)

    score += end_trans
    return score, history

def post_decode(score, history, seq_length):
    batch_size = seq_length.shape[0]
    seq_ends = seq_length - 1
    best_tags_list = []

    for idx in range(batch_size):
        best_last_tag = score[idx].argmax(axis=0)
        best_tags = [int(best_last_tag.asnumpy())]

        for hist in reversed(history[:seq_ends[idx]]):
            best_last_tag = hist[idx][best_tags[-1]]
            best_tags.append(int(best_last_tag.asnumpy()))

        best_tags.reverse()
        best_tags_list.append(best_tags)

    return best_tags_list

CRF层的封装

我们将上述代码封装成一个CRF层：

import mindspore as ms
import mindspore.nn as nn
import mindspore.ops as ops
import mindspore.numpy as mnp
from mindspore.common.initializer import initializer, Uniform

def sequence_mask(seq_length, max_length, batch_first=False):
    range_vector = mnp.arange(0, max_length, 1, seq_length.dtype)
    result = range_vector < seq_length.view(seq_length.shape + (1,))
    if batch_first:
        return result.astype(ms.int64)
    return result.astype(ms.int64).swapaxes(0, 1)

class CRF(nn.Cell):
    def __init__(self, num_tags: int, batch_first: bool = False, reduction: str = 'sum') -> None:
        if num_tags <= 0:
            raise ValueError(f'invalid number of tags: {num_tags}')
        super().__init__()
        if reduction not in ('none', 'sum', 'mean', 'token_mean'):
            raise ValueError(f'invalid reduction: {reduction}')
        self.num_tags = num_tags
        self.batch_first = batch_first
        self.reduction = reduction
        self.start_transitions = ms.Parameter(initializer(Uniform(0.1), (num_tags,)), name='start_transitions')
        self.end_transitions = ms.Parameter(initializer(Uniform(0.1), (num_tags,)), name='end_transitions')
        self.transitions = ms.Parameter(initializer(Uniform(0.1), (num_tags, num_tags)), name='transitions')

    def construct(self, emissions, tags=None, seq_length=None):
        if tags is None:
            return self._decode(emissions, seq_length)
        return self._forward(emissions, tags, seq_length)

    def _forward(self, emissions, tags=None, seq_length=None):
        if self.batch_first:
            batch_size, max_length = tags.shape
            emissions = emissions.swapaxes(0, 1)
            tags = tags.swapaxes(0, 1)
        else:
            max_length, batch_size = tags.shape

        if seq_length is None:
            seq_length = mnp.full((batch_size,), max_length, ms.int64)

        mask = sequence_mask(seq_length, max_length)

        numerator = compute_score(emissions, tags, seq_length-1, mask, self.transitions, self.start_transitions, self.end_transitions)
        denominator = compute_normalizer(emissions, mask, self.transitions, self.start_transitions, self.end_transitions)
        llh = denominator - numerator

        if self.reduction == 'none':
            return llh
        if self.reduction == 'sum':
            return llh.sum()
        if self.reduction == 'mean':
            return llh.mean()
        return llh.sum() / mask.astype(emissions.dtype).sum()

    def _decode(self, emissions, seq_length=None):
        if self.batch_first:
            batch_size, max_length = emissions.shape[:2]
            emissions = emissions.swapaxes(0, 1)
        else:
            batch_size, max_length = emissions.shape[:2]

        if seq_length is None:
            seq_length = mnp.full((batch_size,), max_length, ms.int64)

        mask = sequence_mask(seq_length, max_length)

        return viterbi_decode(emissions, mask, self.transitions, self.start_transitions, self.end_transitions)

BiLSTM+CRF模型

为什么使用双向LSTM

双向LSTM能够同时捕获序列中前后两个方向的依赖关系。在序列标注任务中，当前Token的标签不仅依赖于前面的Token，还可能依赖于后面的Token。通过使用双向LSTM，我们可以更全面地提取序列特征，从而提高模型的表现。

在实现了CRF层之后，我们设计一个双向LSTM+CRF的模型来进行命名实体识别任务的训练。模型结构如下：

nn.Embedding -> nn.LSTM -> nn.Dense -> CRF

具体实现如下：

class BiLSTM_CRF(nn.Cell):
    def __init__(self, vocab_size, embedding_dim, hidden_dim, num_tags, padding_idx=0):
        super().__init__()
        self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx=padding_idx)
        self.lstm = nn.LSTM(embedding_dim, hidden_dim // 2, bidirectional=True, batch_first=True)
        self.hidden2tag = nn.Dense(hidden_dim, num_tags, 'he_uniform')
        self.crf = CRF(num_tags, batch_first=True)

    def construct(self, inputs, seq_length, tags=None):
        embeds = self.embedding(inputs)
        outputs, _ = self.lstm(embeds, seq_length=seq_length)
        feats = self.hidden2tag(outputs)

        crf_outs = self.crf(feats, tags, seq_length)
        return crf_outs

数据准备

我们生成两句例子和对应的标签，并构造词表和标签表：

embedding_dim = 16
hidden_dim = 32

training_data = [(
    "清 华 大 学 坐 落 于 首 都 北 京".split(),
    "B I I I O O O O O B I".split()
), (
    "重 庆 是 一 个 魔 幻 城 市".split(),
    "B I O O O O O O O".split()
)]

word_to_idx = {}
word_to_idx['<pad>'] = 0
for sentence, tags in training_data:
    for word in sentence:
        if word not in word_to_idx:
            word_to_idx[word] = len(word_to_idx)

tag_to_idx = {"B": 0, "I": 1, "O": 2}
len(word_to_idx)

模型训练

实例化模型，选择优化器并将模型和优化器送入Wrapper：

model = BiLSTM_CRF(len(word_to_idx), embedding_dim, hidden_dim, len(tag_to_idx))
optimizer = nn.SGD(model.trainable_params(), learning_rate=0.01, weight_decay=1e-4)
grad_fn = ms.value_and_grad(model, None, optimizer.parameters)

def train_step(data, seq_length, label):
    loss, grads = grad_fn(data, seq_length, label)
    optimizer(grads)
    return loss

将生成的数据打包成Batch，并进行填充：

def prepare_sequence(seqs, word_to_idx, tag_to_idx):
    seq_outputs, label_outputs, seq_length = [], [], []
    max_len = max([len(i[0]) for i in seqs])

    for seq, tag in seqs:
        seq_length.append(len(seq))
        idxs = [word_to_idx[w] for w in seq]
        labels = [tag_to_idx[t] for t in tag]
        idxs.extend([word_to_idx['<pad>'] for i in range(max_len - len(seq))])
        labels.extend([tag_to_idx['O'] for i in range(max_len - len(seq))])
        seq_outputs.append(idxs)
        label_outputs.append(labels)

    return ms.Tensor(seq_outputs, ms.int64), \
            ms.Tensor(label_outputs, ms.int64), \
            ms.Tensor(seq_length, ms.int64)
data, label, seq_length = prepare_sequence(training_data, word_to_idx, tag_to_idx)
data.shape, label.shape, seq_length.shape

预编译模型并训练500个step：

from tqdm import tqdm

steps = 500
with tqdm(total=steps) as t:
    for i in range(steps):
        loss = train_step(data, seq_length, label)
        t.set_postfix(loss=loss)
        t.update(1)

模型评估

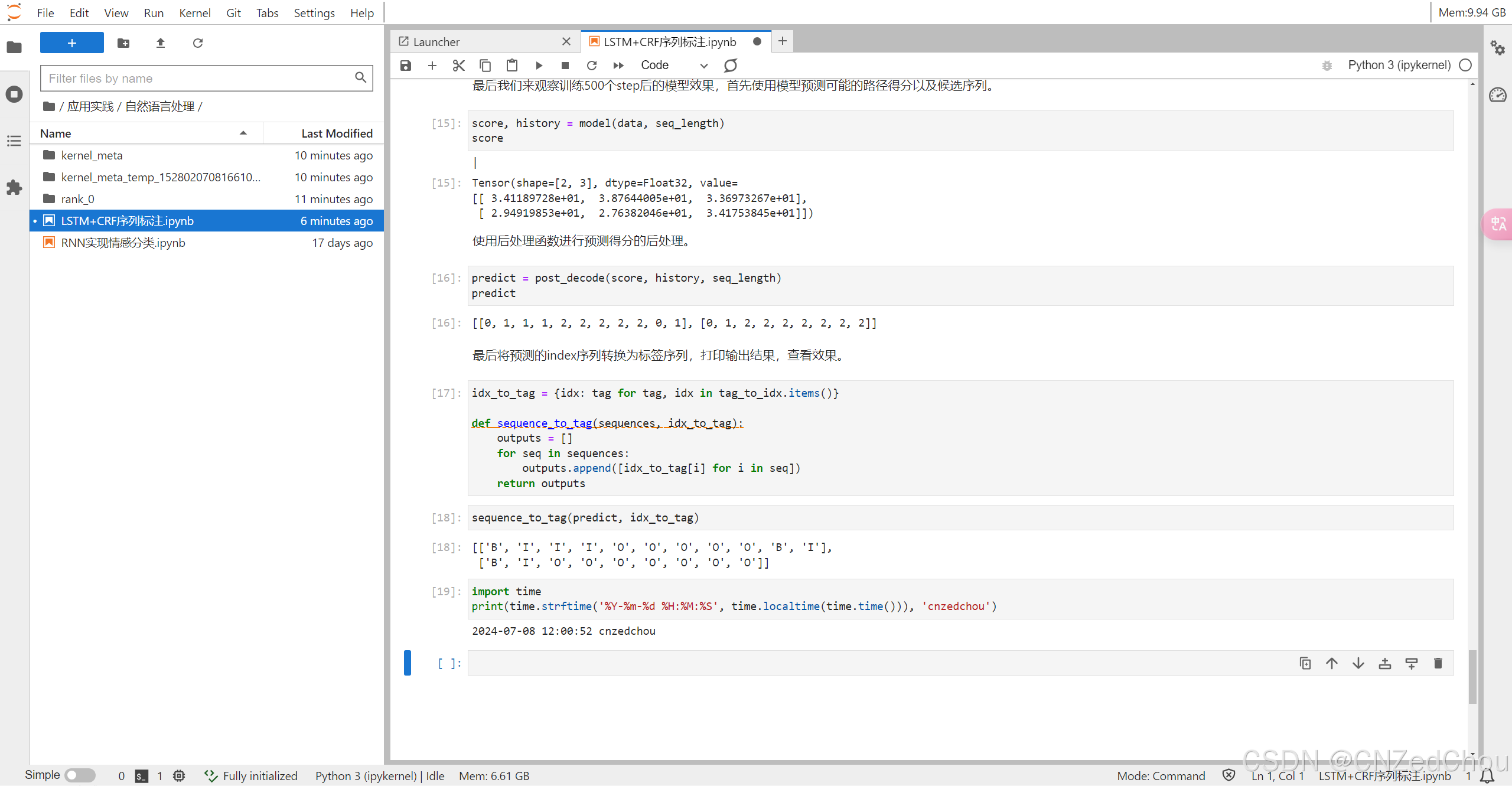
训练完成后，我们使用模型进行预测：

score, history = model(data, seq_length)
score

使用后处理函数进行预测得分的处理：

predict = post_decode(score, history, seq_length)
predict

将预测的index序列转换为标签序列并打印输出结果：

idx_to_tag = {idx: tag for tag, idx in tag_to_idx.items()}

def sequence_to_tag(sequences, idx_to_tag):
    outputs = []
    for seq in sequences:
        outputs.append([idx_to_tag[i] for i in seq])
    return outputs
sequence_to_tag(predict, idx_to_tag)

通过上述步骤，我们成功实现了一个基于LSTM和CRF的序列标注模型，并在命名实体识别任务中进行了应用。希望这篇博客能帮助你更好地理解LSTM和CRF在序列标注中的应用。
在这里插入图片描述