为什么不把这些评价指标直接作为优化的目标函数，特别是MSLE这种特别适合于某中特殊场景的指标？
$\bullet$ 开方均方误差RMSE(Rooted Mean Squared Error)
$$RMSE(y,\hat{y})=\sqrt{\frac{1}{N}\sum _{i=1}^N(y_i-{\hat{y}}_i{)}^2}$$
$\bullet$ 平均绝对值误差MAE(Mean Absolute Error)
$$MAE(y,\hat{y})=\frac{1}{N}\sum _{i=1}^N|(y_i-{\hat{y}}_i)|$$
$\bullet$ 绝对误差中值MedAE(Median Absolute Error)中值的依据是序号，还是值
$$MedAE(y,\hat{y})=median(|y_1-{\hat{y}}_1|,...,|y_N-{\hat{y}}_N|)$$
$\bullet$ 平均平方log误差MSLE(Mean Squared Logarithmic Error)
$$MSLE(y,\hat{y})=\frac{1}{N}\sum _{i=1}^N(log(1+y_i)-log(1+{\hat{y}}_i){)}^2$$
　　log函数在自变量较小时，函数值变化较快，自变量较大时，函数值变化较为平缓，这非常符合人类对价格类数值的敏感变化，当价格在10元量级时，残差为1元，人类会觉得残差较大，而价格在10000元量级时，残差为1元，人类会觉得残差较小。前提条件应该是log的底大于1，而不是属于区间(0,1)，这样函数是单调递增的。上式中的log要加1，应该是要确保自变量大于等于1。PPT上的原 话 ，不好理解 ：当y呈指数增长时可以使用（如计数、一年的平均销量…）

$\bullet$ $R^2$分数($R^2$ Score) 既考虑了预测值和真值之间的差异，也考虑了问题本身之间的差异（这也是scikit-learn线性回归模型的缺省评价标准）。最佳分数为1，越小越不好，肯能为负值。
$$S{S}_{res}(y,\hat{y})=\frac{1}{N}\sum _{i=1}^N(y_i-{\hat{y}}_i{)}^2$$$$S{S}_{tot}(y)=\frac{1}{N}\sum _{i=1}^N(y_i-{\overline{y}}_i{)}^2$$$$R^2(y,\hat{y})=1-\frac{S{S}_{res}(y,\hat{y})}{S{S}_{tot}(y)}$$
$\bullet$ 已解释的方差分数(Explained variance score)：最佳分数位1，越小越不好，应该也可以为负吧？
$$explained\_variance(y,\hat{y})=1-\frac{Var(y-\hat{y})}{Var(y)}$$
$\bullet$ Scikit-Learn中有三种评价模型性能的方式
　　1.estimator的score方法，每个学习器都有score方法，提供一个缺省的评估方法（回归为$R^2$分数）。
　　2.Metric：mettrics模块实现了一些函数，用来评估预测误差。
　　3.Scoring参数：使用交叉验证评估模型的工具有Scoring参数。

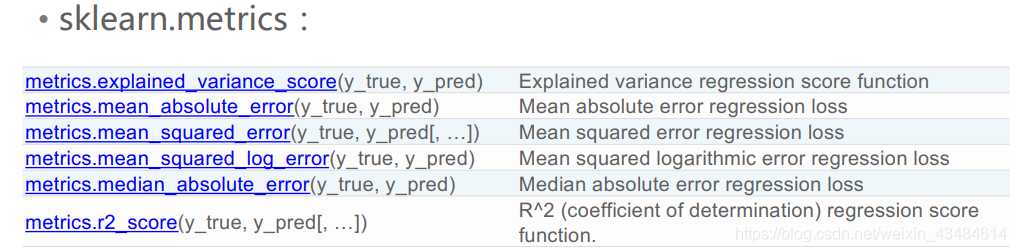
$\bullet$ Scikit-Learn中的metrics的回归评价指标

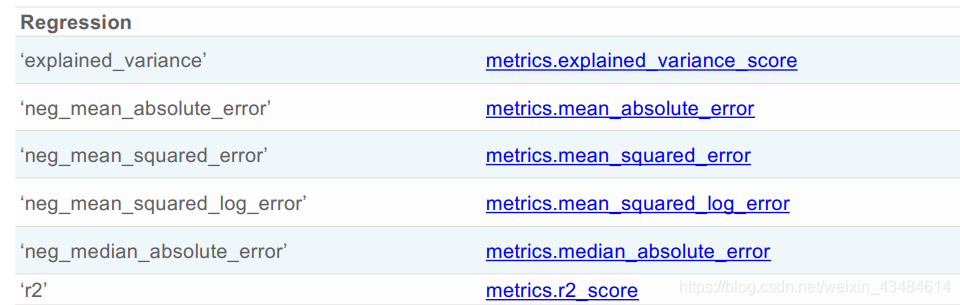
$\bullet$ Scikit-Learn中的Scoring参数

同metrics一一对应