实验2 Python基本图形绘制和数字类型
实验目的和要求: 1. 了解Python turtle库有关知识,学习相关绘图函数;学习Python基本图形绘制有关方法,完成简单图形绘制任务; 2.了解数字类型,掌握数字类型常见函数与操作;通过实例学习并掌握数字类型的具体应用。
1.叠加等边三角形的绘制
描述
叠加等边三角形的绘制
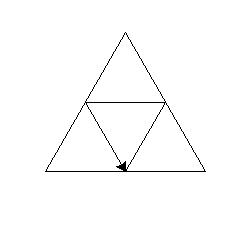
使用turtle库中的turtle.fd函数和turtle.seth函数绘制一个叠加等边三角形,效果下图所示。
同时把运行所生成的图形保存为jpg格式图片,按”序号-姓名-triangle.jpg"命名,上传到附件中。
#triangle.py
import turtle as t
AngleList = [60, -60, -180, -180, 60, 60, -60, -180, -60]
for angle in AngleList:
t.seth(angle)
t.fd(66)
t.done()
2.三位水仙花数计算
描述
“3位水仙花数”是指一个三位整数,其各位数字的3次方和等于该数本身。例如:ABC是一个“3位水仙花数”,则:A的3次方+B的3次方+C的3次方 = ABC。
请按照从小到大的顺序输出所有的3位水仙花数,请用一个“逗号+空格”分隔输出结果。
注意:这是一个OJ题目,输出格式要严格一致,最后一位水仙花数后没有逗号。
#PPDI.py
Pdi = []
for A in range(10):
for B in range(10):
for C in range(10):
if A**3 + B**3 + C**3 == A * 100 + B * 10 + C and len(
str(A * 100 + B * 10 + C)) == 3:
Pdi.append(100 * A + 10 * B + C)
print(', '.join(str(i) for i in Pdi))
3. 快乐的数字
描述
描述
编写一个算法来确定一个数字是否“快乐”。 快乐的数字按照如下方式确定:从一个正整数开始,用其每位数的平方之和取代该数,并重复这个过程,直到最后数字要么收敛等于1且一直等于1,要么将无休止地循环下去且最终不会收敛等于1。能够最终收敛等于1的数就是快乐的数字。
例如: 19 就是一个快乐的数字,计算过程如下:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
当输入时快乐的数字时,输出True,否则输出False。
#happynumber.py
#参考:https://www.cnblogs.com/du001011/p/10476867.html
a = input()
li = list(str(a))
while (a != 1):
num = list(str(a))
a = 0
for i in num:
a = a + int(i)**2
if a in li:
print(False)
exit()
li.append(a)
print(True)