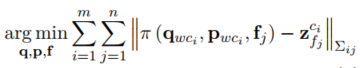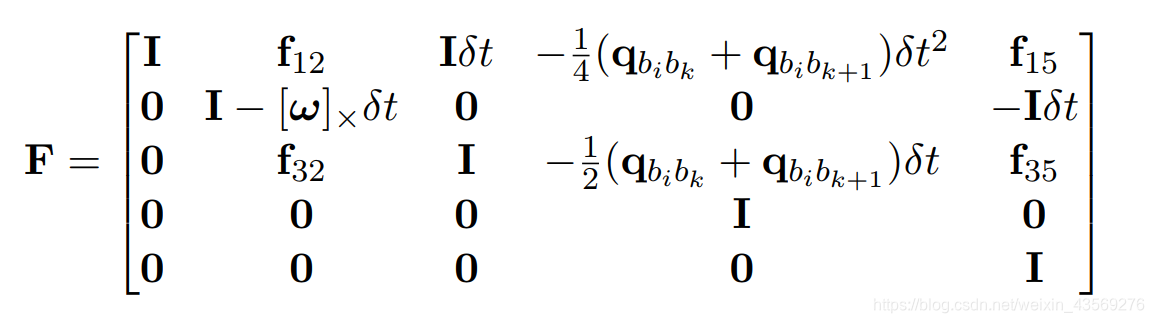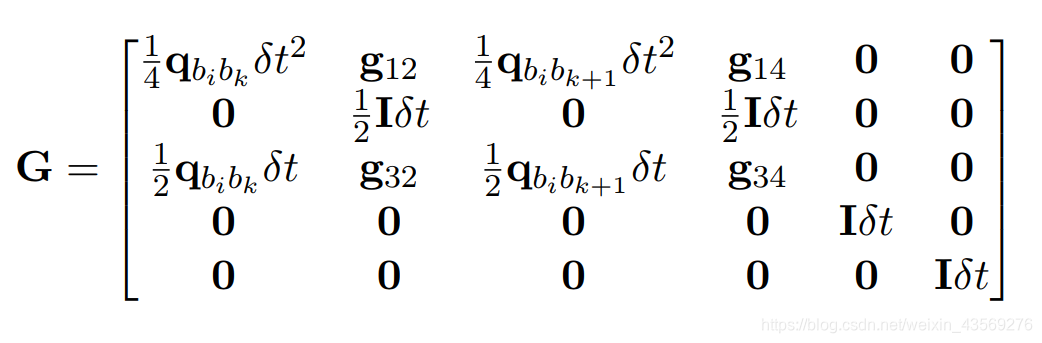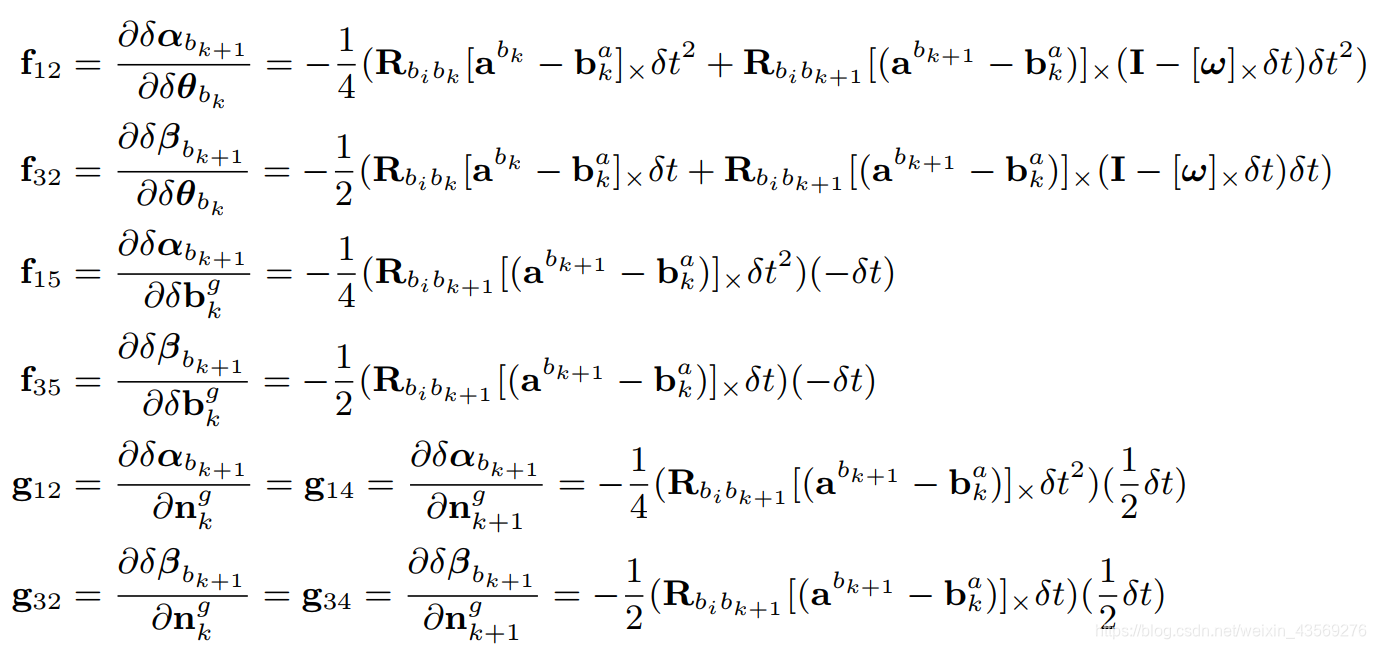1. 基于Bundle Adjustment的VIO融合

1.1 为什么需要融合

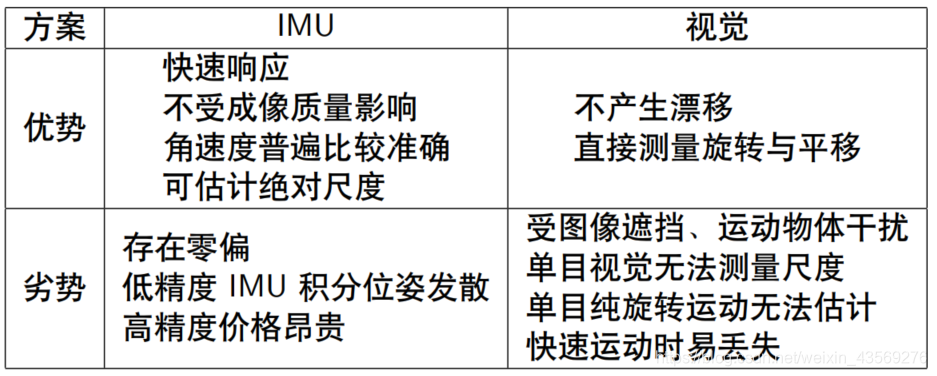
一、IMU 与视觉定位方案优势与劣势对比：
  视觉和 IMU 定位方案存在一定互补性质：
  IMU 适合计算短时间、快速的运动；视觉适合计算长时间、慢速的运动。同时，可利用视觉定位信息来估计 IMU 的零偏，减少 IMU 由零偏导致的发散和累积误差；反之， IMU 可以为视觉提供快速运动时的定位。

1.2 视觉与IMU融合两类方案：

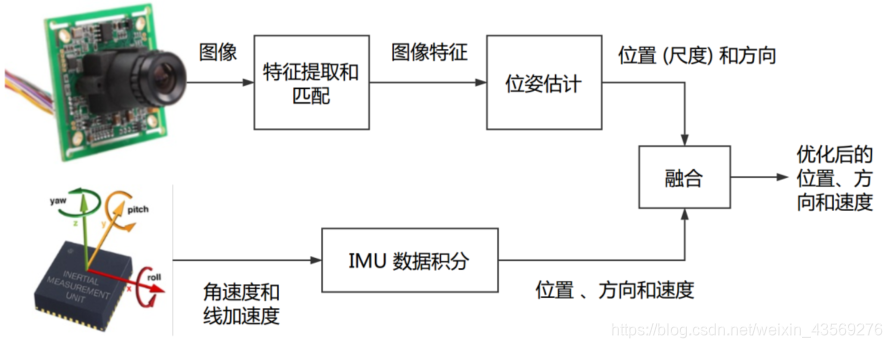
一、松耦合：
  将 IMU 定位与视觉/GNSS 的位姿直接进行融合，融合过程对二者本身不产生影响，作为后处理方式输出。典型方案为卡尔曼滤波器。

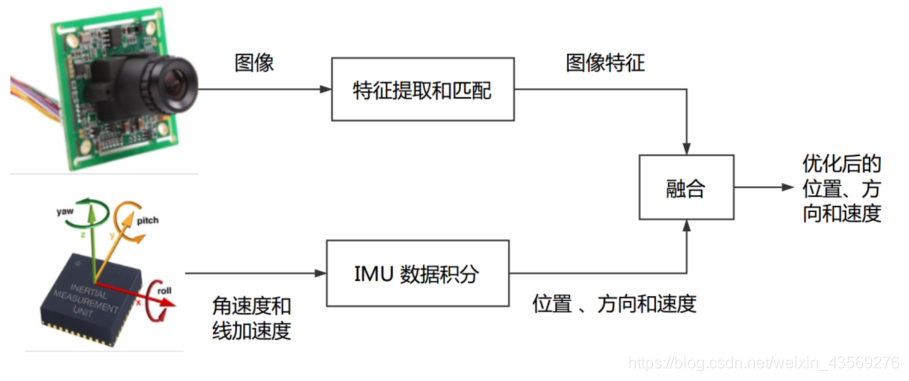
二、紧耦合：
  融合过程本身会影响视觉和 IMU 中的参数（如 IMU 的零偏和视觉的尺度）。典型方案为 MSCKF 和非线性优化。

三、松耦合和紧耦合对比：

1. 单纯凭（单目）视觉或 IMU 都不具备估计 Pose 的能力：视觉存
   在尺度不确定性、 IMU 存在零偏导致漂移
2. 松耦合中，视觉内部 BA 没有 IMU 的信息，在整体层面来看不是
   最优的
3. 紧耦合可以一次性建模所有的运动和测量信息，更容易达到最优。

1.3 视觉SLAM中的BA问题

  在视觉SLAM中，我们通过最小化路标点的重投影误差，实现对相机位姿的约束。（路标点为跟踪的特征点或者光流点）

  对于VSLAM中的BA问题，有以下已知条件：
状态量的初始值： 特征点的三维坐标；相机的位姿
系统测量值： 特征点在不同图像上的像素坐标
  BA问题就是利用测量值来实现对初始状态量的最优估计。
  构建误差函数，利用最小二乘得到状态量的最优估计，使重投影误差最小。

1.4 VIO信息融合考虑的问题

  将IMU融入到视觉里程计中，除了要最小化特征点的重投影误差以外，还需要考虑如下问题：

1. 相机与IMU的外参，包括旋转和平移
2. 相机和IMU的帧率不同，如何实现两者数据上的融合
3. IMU从 $b_1$ 到 $b_2$ 时，有测量值 $z_{b_1{b}_2}$，如何构建IMU的测量误差函数
4. 位姿的来源有IMU测量和视觉测量，如何设定多个信息源权重
5. 对于融合信息后构建的误差函数，如何求解

2.VIO残差函数的构建

2.1 最小二乘问题

  目的是找到一个 $n$ 维的变量 $n^{\ast }\in {\mathbb{R}}^n$，使得损失函数 $F(x)$ 取局部最小值：
$$F(x)=\frac{1}{2}\sum _{i=1}^m(f_i(x){)}^2$$   其中 $f_i$ 是残差函数，如测量值和预测值之间的差，且有 $m\ge n$即观测数量大于变量的维度，使问题具有很好的约束（一般为超定方程）。局部最小值指对任意 $||x-x^{\ast }||<\delta$，有 $F(x^{\ast })\le F(x)$。

2.2 带权重（方差）的权重计算

  为了将不同传感器的信息有效的融合在一起，将残差方程变为如下形式：
$$r=||\mathrm{f}(x)|{|}_{\Sigma }^2={\mathrm{f}}^T(x){\Sigma }^{-1}\mathrm{f}(x)$$   其中，$\mathrm{f}(x)$ 服从高斯分布，其协方差为 $\Sigma$。这里乘上协方差矩阵的逆。
  协方差反应了一个测量数据的不确定度，如果协方差 $\Sigma$ 越小，代表数据不确定度越小，可信度越高，在优化的过程中我们更应该关注可信度高的数据。$\Sigma$ 越小， ${\Sigma }^{-1}$越大，则该项测量误差在总的残差方程 $r$ 中的权重也就越大。

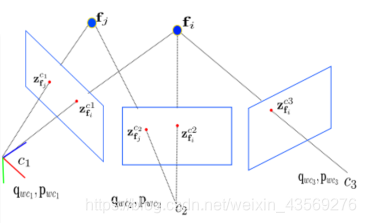
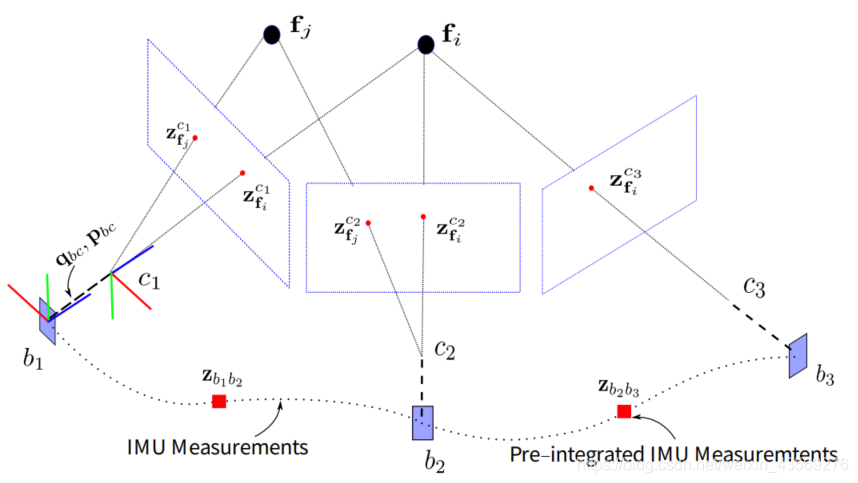
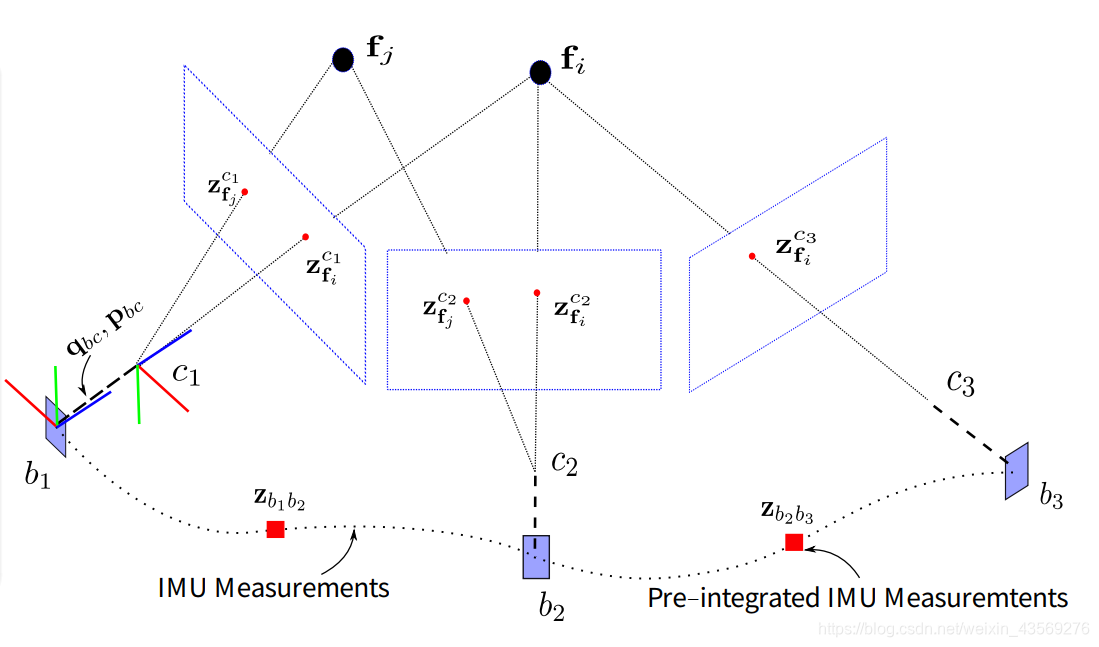
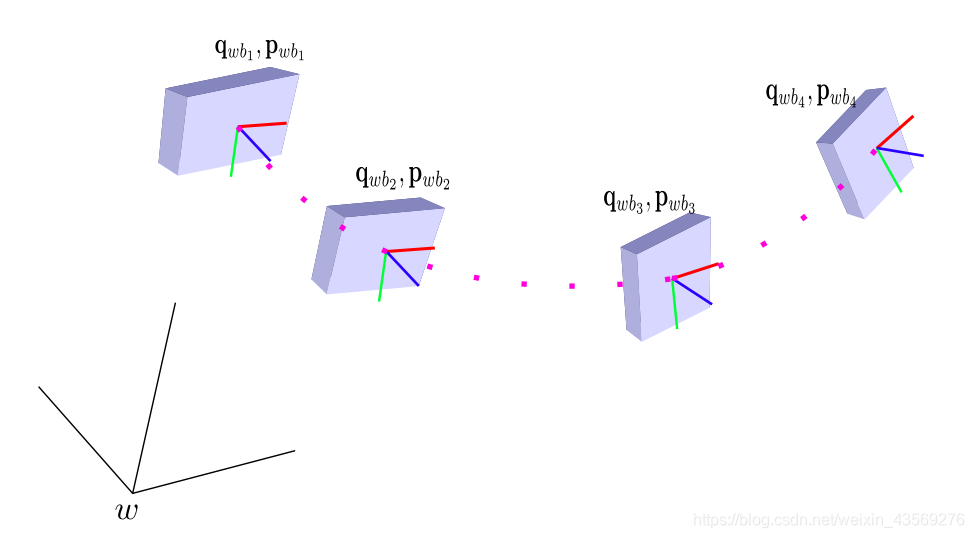
2.3 基于滑动窗口的VIO Bundle Adjustment

  在滑动窗口的VIO BA中，设定各个参数的符号如上图所示。
  为了节约计算量，采用滑动窗口的形式去计算 Bundle Adjustment。滑动窗口中只负责优化一定数量帧的数据，在窗口中帧的数量达到设定值后，每新增一帧，都要丢到窗口中最前面的一帧。但是最前面的一帧不能直接丢掉，因为其存在有效的观测数据和信息。这里就需要将之前观测的信息整合成一个先验的信息，一起放到后面的数据优化中。

一、基于滑窗的VIO优化方程：
$$\begin{gathered} \underset{\mathcal{X}}{\min }\underset{prior}{\underbrace{\rho (||r_p-J_p\mathcal{X}|{|}_{{\Sigma }_p}^2)}}+\sum _{i\in B}\underset{IMUerror}{\underbrace{\rho (||r_b(z_{b_i{b}_{i+1}},\mathcal{X})|{|}_{{\Sigma }_{b_i{b}_{i+1}}}^2)}} \\ +\underset{Imageerror}{\underbrace{\sum _{(i,j)\in F}\rho (||r_f(z_{f_j}^{c_i},\mathcal{X})|{|}_{{\Sigma }_{f_j}^{c_i}}^2)}} \end{gathered}$$
  通过最小化这些状态量残差值的和，以达到估计最优位姿的目的。

二、系统需要优化的状态量
  系统状态量定义如下：
$$\begin{gathered} \mathcal{X}=[x_n,x_{n+1},...,x_{n+N},{\lambda }_m,{\lambda }_{m+1},...,{\lambda }_{m+M}] \\ {x}_i=[p_{w{b}_i},q_{w{b}_i},v_i^w,b_a^{b_i},b_g^{b_i}{]}^T,i\in [n,n+N] \end{gathered}$$   其中 $x$ 为相机的姿态，$\lambda$为观测到的路标点。
   $x_i$ 包括 $i$ 时刻 IMU 机体在惯性坐标系中的位置 $p$、姿态 $q$、速度 $v$，以及 IMU 机体坐标系中的加速度偏置量估计 $b_a$ 和角速度的偏置量估计 $b_g$。
  $n,m$ 分别时机体状态量和路标在滑动窗口里的起始时刻，即滑动窗口从第 $n$ 帧 第 $m$ 个路标为起始点。
  $N$ 为滑动窗口中关键帧数量， $M$ 是被滑动窗口内所有关键帧观测到的路标数量。

2.4 视觉重投影误差

一、重投影误差的定义：
  定义一个特征点在归一化相机坐标系下的估计值与观测值的差为重投影误差。
$$r_c=\left[\begin{array}{c}\frac{x}{z}-u\\ \frac{y}{z}-v\end{array}\right]$$其中，待估计的状态量为特征点的三维空间坐标 $(x,y,z{)}^T$，观测值
$(u,v{)}^T$ 为特征在相机归一化平面的坐标。

二、逆深度参数化：
  特征点在归一化相机坐标系与在相机坐标系下的坐标关系为：
$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\frac{1}{\lambda }\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$$  其中，$\lambda =1/z$ 称为逆深度。之所以使用 $1/z$ 逆深度的方式来表达，是因为当 $z\to \infty$ 时，$x/z,y/z$ 无法表示，而使用逆深度有 $\lambda \to 0$，可以很好的表示任何值。且使用逆深度时，重投影误差函数更接近于高斯分布。

三、VIO中基于逆深度的重投影误差：
  特征点逆深度在第 $i$ 帧中第一次被观测到，之后又在第 $j$ 帧中又被观测到，预测其在第 $j$ 中的坐标为：
$$\left[\begin{array}{c}{x}_{c_j}\\ y_{c_j}\\ z_{c_j}\\ 1\end{array}\right]=T_{bc}^{-1}{T}_{w{b}_j}^{-1}{T}_{w{b}_i}{T}_{bc}\left[\begin{array}{c}\frac{1}{\lambda }{u}_{c_i}\\ \frac{1}{\lambda }{v}_{c_i}\\ \frac{1}{\lambda }\\ 1\end{array}\right]$$  式中，$T_{bc}$ 为相机坐标系到 IMU坐标系的外参，$T_{w{b}_i}$ 和 $T_{w{b}_j}$ 分别为第 $i$ 帧和第 $j$ 帧的 IMU坐标系到世界坐标系的变换矩阵。（运算逻辑为：第 $i$ 帧中特征点的在相机坐标系中的坐标，转换到第 $i$ 帧的 body 坐标系，转换到世界坐标系，再转换到第 $j$ 帧的body 坐标系，再根据外参由 body 坐标系转换到第 $j$ 帧的相机坐标系）
  以上式由第 $i$ 帧特征点在相机坐标系中的坐标，推算出其在第 $j$ 帧相机坐标系中的坐标为预测值，以 第 $j$ 帧中特征点的像素坐标系为观测值。则视觉重投影误差为：
$$r_c=\left[\begin{array}{c}\frac{x_{c_j}}{z_{c_j}}-u_{c_j}\\ \frac{y_{c_j}}{z_{c_j}}-v_{c_j}\end{array}\right]$$
四、重投影误差协方差矩阵的选择
  通常，我们假设特征点观测值为 $f$ ，其误差为 1 个像素。则假设观测服从正态分布 $\mathcal{N}(f,1)$。可以以算出对应的协方差矩阵 $\Sigma$ 。则对于残差 $r$ 有：
$$r=r_c^T{\Sigma }^{-1}{r}_c$$

2.5 IMU误差

  VIO中需要融合 IMU 积分的误差，那么首先我们要对 IMU 积分的误差进行建模，见下一节。

3 IMU预积分模型与误差处理

3.1 IMU测量值积分

  IMU的真实值为 $\omega ,a$，测量值为 $\tilde{\omega },\tilde{a}$，根据 IMU 的测量模型，则有：
$$\begin{gathered} {\tilde{\omega }}^b={\omega }^b+b^g+n^g \\ {\tilde{a}}^b=q_{bw}(a^w+g^w)+b^a+n^a \end{gathered}$$  上标 $g$ 表示 gyro， $a$ 表示 acc，$w$ 表示在世界坐标系 world，$b$ 表示 imu 本体坐标系 body。IMU 的真实值为 $\omega ,a$，测量值为 $\tilde{\omega },\tilde{a}$
  P(ose),v(elocity),q(uaternion) 对时间的导数可写成：
$$\begin{gathered} {\dot{P}}_{w{b}_t}={\mathrm{v}}_t^w \\ {\dot{\mathrm{v}}}_t^w=a_t^w \\ {\dot{q}}_{w{b}_t}=q_{w{b}_t}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\omega }^{b_t}\end{array}\right] \end{gathered}$$
  从第 $i$ 时刻的 PVQ 对 IMU 的测量值进行积分得到第 $j$ 时刻的 PVQ:
$$\begin{gathered} P_{w{b}_j}=P_{w{b}_i}+{\mathrm{v}}_i^w\Delta t+{\iint }_{t\in [i,j]}(q_{w{b}_t}{a}^{b_t}-g^w)d{t}^2 \\ {\mathrm{v}}_j^w={\mathrm{v}}_i^w+{\int }_{t\in [i,j]}(q_{w{b}_t}{a}^{b_t}-g^w)dt \\ {q}_{w{b}_j}={\int }_{t\in [i,j]}{q}_{w{b}_i}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\omega }^{b_t}\end{array}\right]dt \end{gathered}$$  这样一步步的积分，在优化过程中，每次 $q_{w{b}_t}$ 优化更新后，都需要重新进行积分(re-propagation)，运算量较大。

3.2 IMU预积分

  利用如下公式，将IMU积分模型转换为预积分模型：
$$q_{w{b}_t}=q_{w{b}_i}\otimes q_{b_i{b}_t}$$  其含义为：将IMU积分模型分为 $q_{w{b}_i}$ 和 $q_{b_i{b}_t}$，$q_{w{b}_i}$为 $i$ 时刻 IMU 坐标系到相机坐标系的变换，$q_{b_i{b}_t}$ 为 $t$ 时刻 IMU 坐标系相对于 $i$ 时刻 IMU 坐标系的变换。这样就把本来相互关联的 IMU 积分轨迹进行分段，然后再根据 $q_{w{b}_i}$ 进行拼接即可。
  可以算出 $q_{b_i{b}_t}$，其只与IMU的积分有关，与世界坐标系无关，所以这一部分值是固定的，不参与优化。这样我们优化 $q_{w{b}_i}$ 就可以优化 $q_{w{b}_t}$ ，则不需要重新计算整个积分公式。
  则由 3.1 中的积分公式，将PVQ积分公式中的积分项变成 $j$ 时刻相对于 $i$ 时刻的姿态，而不是相对于世界坐标系。可以推导出预积分公式：
$$\begin{array}{rl}& P_{w{b}_j}=P_{w{b}_i}+v_i^w\Delta t-\frac{1}{2}{g}^w\Delta t^2+q_{w{b}_i}{\iint }_{t\in [i,j]}(q_{b_i{b}_j}{a}^{b_t})d{t}^2\\ & v_j^w=v_i^w-g^w\Delta t+q_{w{b}_i}{\int }_{t\in [i,j]}(q_{b_i{b}_j}{a}^{b_t})d{t}^2\\ & q_{w{b}_j}=q_{w{b}_i}{\int }_{t\in [i,j]}{q}_{b_i{b}_t}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\omega }^{b_t}\end{array}\right]dt\end{array}$$  预积分的含义：
  每次IMU的积分都是 $t_{(i<t<=j)}$ 时刻相对于 $i$ 时刻的IMU姿态的积分，而与世界坐标系无关。IMU积分都在IMU坐标系中完成，当需要其相对于世界坐标系的位姿关系时，再乘上 $i$ 时刻的变换 $q_{w{b}_i}$ 即可。这样就将IMU积分从世界坐标系中分离。我们对比 3.1 节和 3.2 节的公式，可以发现 $q_{w{b}_t}$ 从积分公式中分离了出来，不再参与积分。
  个人理解为：
  本来IMU积分是在世界坐标系中进行积分，一旦一个 IMU相对于世界坐标系的变换 $q_{w{b}_t}$ 发生了改变，比如在积分完成后、优化过程中，$q_{w{b}_0}$ 发生了改变，则由于后面所有的积分量在 $q_{w{b}_0}$ 所定义的变换中，则需要从 $q_{w{b}_0}$ 时刻利用积分公式一个一个的重新积分，这个过程为重传播。
  但是利用预积分，相当于实在第 $i$ 时刻和第 $j$ 时刻之间的积分量视为一个数据段，这个数据段只保留这一段数据内的积分量，即 IMU 在body坐标系中的相对变换关系。这样相当于将整个 IMU 积分曲线进行了分段处理，这样在曲线某一点位置发生变化时，我们只需要对不同时刻的位置节点 $q_{w{b}_i}$ 进行相对位置关系的调整即可，则不要进行重积分。相当于 IMU 的预积分提供了不同节点 $q_{w{b}_i}$ 之间的约束关系。

3.3 预积分量

  预积分量只与 IMU 测量值有关，它将一段时间内的 IMU 测量数据直接积分起来就得到了预积分量：
$$\begin{array}{rl}& {\alpha }_{b_i{b}_j}={\iint }_{t\in [i,j]}(q_{b_i{b}_j}{a}^{b_t})d{t}^2\\ & {\beta }_{b_i{b}_j}={\int }_{t\in [i,j]}(q_{b_i{b}_j}{a}^{b_t})dt\\ & q_{b_i{b}_j}={\int }_{t\in [i,j]}{q}_{b_i{b}_t}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\omega }^{b_t}\end{array}\right]dt\end{array}$$   式中，${\alpha }_{b_i{b}_j}$ 表示两时刻间位移的变化，${\beta }_{b_i{b}_j}$ 表示速度的变化，$q_{b_i{b}_j}$ 表示姿态的变化。
  重新整理 PVQ 的预积分公式，有：
$$\left[\begin{array}{c}{P}_{w{b}_j}\\ v_j^w\\ q_{w{b}_j}\\ b_j^a\\ b_j^g\end{array}\right]=\left[\begin{array}{c}{P}_{w{b}_i}+v_i^w\Delta t-\frac{1}{2}{g}^w\Delta t^2+q_{w{b}_i}\cdot {\alpha }_{b_i{b}_j}\\ v_i^w-g^w\Delta t+q_{w{b}_i}\cdot {\beta }_{b_i{b}_j}\\ q_{w{b}_i}\otimes q_{b_i{b}_j}\\ b_i^a\\ b_i^g\end{array}\right]$$  $b^a,b^g$ 为偏置 $bias$，同时由于 $i$ 时刻和 $j$ 时刻间隔很短，假设两时刻间 $bias$ 不变，则有 $b_j^a=b_i^a,b_j^g=b_i^g$。
(积分公式中的是点乘和$\otimes$的问题，具体看代码)
  P.S. 这里有 $-\frac{1}{2}{g}^w\Delta t^2$ 和 $-g^w\Delta t$ 是要减去两个时刻之间世界坐标系下的重力加速度分量对位移和速度的影响。

3.4 IMU预积分误差

  利用一段时间内 IMU 构建的预积分量作为测量值，利用两个时刻之间的状态量的约束，构建误差：
$${\left[\begin{array}{c}{r}_p\\ r_q\\ r_v\\ r_{b_a}\\ r_{b_g}\end{array}\right]}_{15\times 1}=\left[\begin{array}{c}{q}_{b_{i}w}(P_{w{b}_j}-P_{w{b}_i}-v_i^w\Delta t+\frac{1}{2}{g}^w\Delta t^2)-{\alpha }_{b_i{b}_j}\\ 2[q_{b_j{b}_i}\otimes (q_{b_{i}w}\otimes q_{w{b}_j}){]}_{xyz}\\ q_{b_{i}w}(v_j^w-v_i^w+g^w\Delta t)-{\beta }_{b_i{b}_j}\\ b_j^a-b_i^a\\ b_j^g-b_i^g\end{array}\right]$$  式中，所有与世界坐标系有关的量是待优化量，所以可以构建出相应的误差函数。
  上面误差中位移，速度，偏置都是直接相减得到。而关于四元数的旋转误差 $r_q$，使用 $[\cdot {]}_{xyz}$ 表示只取四元数的虚部 $(x,y,z)$组成的三维向量。 这里之所以将虚部取出来×2，是因为我们在假设旋转角度很小时，四元数的实部接近 1，则用虚部就可以表达旋转。

3.5 预积分的离散形式

  采用中值积分方法，即使用相邻两个时刻 $k$ 和 $k+1$ 时刻的测量值的平均值来计算积分。
则有：
$$\begin{array}{rl}a& =\frac{1}{2}[q_{b_i{b}_k}(a^{b_k}-b_k^a)+q_{b_i{b}_{k+1}}(a^{b_{k+1}}-b_k^a)]\\ \omega & =\frac{1}{2}[({\omega }^{b_k}-b_k^g)+({\omega }^{b_{k+1}}-b_k^g)]\\ q_{b_i{b}_{k+1}}& =q_{b_i{b}_k}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}\omega \delta t\end{array}\right]\\ {\alpha }_{b_i{b}_{k+1}}& ={\alpha }_{b_i{b}_k}+{\beta }_{b_i{b}_k}\delta t+\frac{1}{2}a\delta t^2\\ {\beta }_{b_i{b}_{k+1}}& ={\beta }_{b_i{b}_k}+a\delta t\\ b_{k+1}^a& =b_k^a+n_{b_k^a}\delta t\\ b_{k+1}^g& =b_k^g+n_{b_k^g}\delta t\end{array}$$

3.6 预积分的协方差传递

  IMU 的测量是具有噪声的（高斯白噪声），在一段时间内，具有多个 IMU 测量值，如0.1s内有20个 IMU 的测量值。在使用时，我们使用这20个测量值积分成的一个测量值，那么这一个积分值也是有噪声的，这个积分值的噪声我们如何得到，它是如何由一个个测量值的噪声传递过来的呢？
  一、协方差传递：
  假设由线性系统 $y=Ax$ , $x\in \mathcal{N}(0,{\Sigma }_x)$ ，则有 ${\Sigma }_y=A{\Sigma }_x{A}^T$
$$\begin{array}{rl}{\Sigma }_y& =E((Ax)(Ax{)}^T)\\ & =E(Ax{x}^{T}A)\\ & =A{\Sigma }_x{A}^T\end{array}$$
  二、误差的线性传递方程：
  假设已知相邻时刻误差的线性传递方程：
$${\eta }_{ik}=F_{k-1}{\eta }_{ik-1}+G_{k-1}{n}_{k-1}$$  比如：状态量误差为 ${\eta }_{ik}=[\delta {\theta }_{ik},\delta v_{ik},\delta p_{ik}]$，测量噪声为 $n_k=[n_k^g,n_k^a]$。
  误差的传递由两部分组成：1、上一时刻的误差传递给当前时刻；2、上一时刻的测量噪声传递给当前时刻。
  则误差传递的协方差矩阵为：
$${\Sigma }_{ik}=F_{k-1}{\Sigma }_{ik-1}{F}_{k-1}^T+G_{k-1}{\Sigma }_n{G}_{k-1}^T$$  其中，${\Sigma }_n$ 是测量噪声的协方差矩阵，通过 IMU 标定得到；方差${\Sigma }_{ik-1}$ 从 $i$ 时刻开始进行递推，${\Sigma }_{ii}=0$。
  三、基于一阶泰勒展开的误差递推方程：
  对于线性高斯系统，我们通过线性传递公式得到误差的传递方程。但是 VIO 系统是一个高度非线性的系统，要得到误差传递公式，首先要对系统进行一阶泰勒线性近似。
  令状态量为 $x=\hat{x}+\delta x$，其中，$\hat{x}$ 为真值，$\delta x$ 为误差。
  假设非线性系统的输入量为 $u$，其噪声为 $n$，则对于非线性系统 $x_k=f(x_{k-1},u_{k-1})$，对其进行一阶泰勒展开，得到：
$$\begin{array}{rl}{x}_k& =f(x_{k-1},u_{k-1})\\ {\hat{x}}_k+\delta x_k& =f({\hat{x}}_{k-1}+\delta x_{k-1},{\hat{u}}_{k-1}+n_{k+1})\\ {\hat{x}}_k+\delta x_k& =f({\hat{x}}_{k-1},{\hat{u}}_k)+F\delta x_{k-1}+G{n}_{k-1}\end{array}$$  这样，我们就有误差的传递方程：
$$\delta x_k=F\delta x_{k-1}+G{n}_{k-1}$$  其中 $F$ 是状态量 $x_k$ 对状态量 $x_{k-1}$ 的雅可比矩阵，$G$ 是状态量 $x_k$ 对输入量 $u_k$ 的雅可比矩阵。
  计算出两个雅可比矩阵 $F$ 和 $G$ 的形式，就可以得到误差的传递方程。
  四、雅可比矩阵的形式：
  将测量噪声加入到预积分公式中去，得到：
$$\begin{array}{rl}\omega & =\frac{1}{2}[({\bar{\omega }}^{b_k}+n_k^g-b_k^g)+({\bar{\omega }}^{b_{k+1}}+n_{k+1}^g-b_k^g)]\\ a& =\frac{1}{2}[q_{b_i{b}_k}({\bar{a}}^{b_k}+n_k^a-b_k^a)+q_{b_i{b}_{k+1}}(a^{b_{k+1}}+n_{k+1}^a-b_k^a)]\\ q_{b_i{b}_{k+1}}& =q_{b_i{b}_k}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}\omega \delta t\end{array}\right]\\ {\alpha }_{b_i{b}_{k+1}}& ={\alpha }_{b_i{b}_k}+{\beta }_{b_i{b}_k}\delta t+\frac{1}{2}a\delta t^2\\ {\beta }_{b_i{b}_{k+1}}& ={\beta }_{b_i{b}_k}+a\delta t\\ b_{k+1}^a& =b_k^a+n_{b_k^a}\delta t\\ b_{k+1}^g& =b_k^g+n_{b_k^g}\delta t\end{array}$$  构建的误差传递方程为：
$$\left[\begin{array}{c}\delta {\alpha }_{b_{k+1}}\\ \delta {\theta }_{b_{k+1}}\\ \delta {\beta }_{b_{k+1}}\\ \delta b_{b_{k+1}}^a\\ \delta b_{b_{k+1}}^g\end{array}\right]=F\left[\begin{array}{c}\delta {\alpha }_{b_k}\\ \delta {\theta }_{b_k}\\ \delta {\beta }_{b_k}\\ \delta b_{b_k}^a\\ \delta b_{b_k}^g\end{array}\right]+G\left[\begin{array}{c}{n}_k^a\\ n_k^g\\ n_{k+1}^a\\ n_{k+1}^g\\ n_{b_k^a}\\ n_{b_k^g}\end{array}\right]$$  其中 $F$ 和 $G$ 的形式如下：

4.VIO系统残差Jacobian

（还未理解，未来补）