采样:模型会在Latent Space中生成一个完全随机的图像,然后噪声预测器会从图像中减去预测的噪声。随着这个步骤的不断重复,最终得到一个清晰的图像。
Stable Diffusion在每个步骤中都会生成一张新的采样后的图像,整个去噪的过程,即为采样,使用的采样手段,即为采样器或称为采样方法
逆向采样过程:
在生成阶段,目标是从纯噪声状态开始,通过一系列步骤反向模拟扩散过程以去除噪声并生成清晰图像。这就是采样的核心环节。为了实现这一点,模型需要解一个与扩散过程相反的微分方程或随机过程,以便逐次减少噪声并重构出接近原始数据的概率分布中的样本。
为什么要求解微分方程?(微分方程在这里起着描述数据退化和复原过程的作用。对于Stable Diffusion模型,特别是基于常微分方程(ODE)或随机微分方程(SDE)的变种,模型需要能够预测在任意噪声水平下如何“去噪”给定的输入图像。通过求解这些微分方程,模型能够在每一步预测最优的更新量,从而使得当前的中间态更接近于真实数据而不是噪声。这种迭代去噪的方式允许模型控制生成过程,并最终得到高质量的输出图像。)
举个栗子,最简单的Euler采样
import numpy as np
# 定义目标函数(假设我们有一个线性ODE dy/dt = f(t, y))
def f(t, y):
# 这里以dy/dt = -y + x + 1为例
# 实际应用中请替换为你的函数f
x = t * 2 # 假设x与t有关的一个示例项
return -y + x + 1
def euler(f, t0, y0, h, N):
"""
Euler方法实现
参数:
f : 目标函数
t0 : 初始时间
y0 : 初始状态
h : 时间步长
N : 总步数
返回:
t_list : 时间点列表
y_list : 对应时间点的状态列表
"""
t_list = np.arange(t0, t0 + (N + 1) * h, h)
y_list = np.zeros(N + 1)
y_list[0] = y0
for n in range(N):
y_list[n + 1] = y_list[n] + h * f(t_list[n], y_list[n])
return t_list, y_list
# 示例调用Euler方法
t0 = 0.0
y0 = 1.0 # 初始条件
h = 0.1 # 时间步长
N = 100 # 步数,根据实际情况调整以保证精度和覆盖所需的时间区间
t_values, y_values = euler(f, t0, y0, h, N)
# 输出结果
print("Time points:", t_values)
print("Solution values at each time point:", y_values)
#复习一下数学常识
#在Euler方法中,对于一阶常微分方程:
#dy/dt = f(t, y) 其中 y 是时间 t 的函数,而 f 是描述 y 对时间变化率的函数。
#Euler方法的基本思想是通过以下近似公式来计算下一个时间点的状态:
#y_{n+1} = y_n + h * f(t_n, y_n)
#其中:
#y_n 是在时间点 t_n 处的状态(即当前已知状态),
#h 是时间步长,
#f(t_n, y_n) 是在当前状态和时间下的导数值(变化率),
#y_{n+1} 是通过向前推一步得到的下一个时间点的状态估计值,即 t_{n+1} = t_n + h 时刻的状态。
这个例子展示了使用Euler方法对给定的目标函数 f 进行离散化求解
Heun-比Euler更精确但更慢
LMS(Linear multi-step method,线性多步求解)-速度与Euler相同,可能会更准确
Ancestral系列
有些sampler的名字里会带一个a,这就代表他们是Ancestral sampler祖先采样器,祖先采样器会在每一步之间向图片添加随机的噪声,因而采样结果具有一定的随机性,难以稳定复现结果。
有些采样器名字里没有带a,但是也会添加随机噪声(例如DDIM)。
采用祖先采样器生成的过程中,即便到了最后几个采样步骤,图像也在发生一定的变化(因为有新的噪声添加进来)。(即结果不收敛)
如果想在图片里引入一定的变化,更可控的方式是采用variation seed。
Karras系列
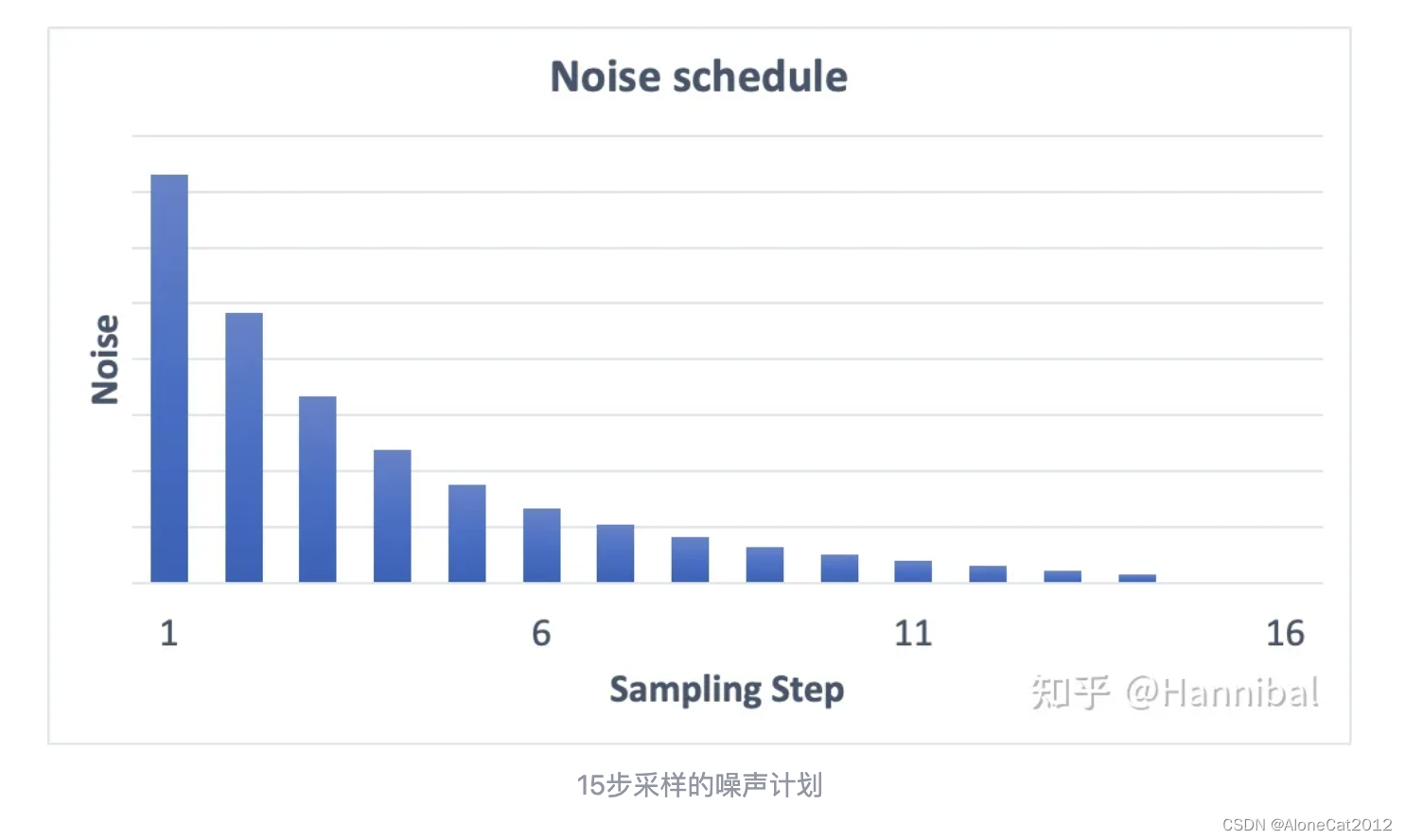
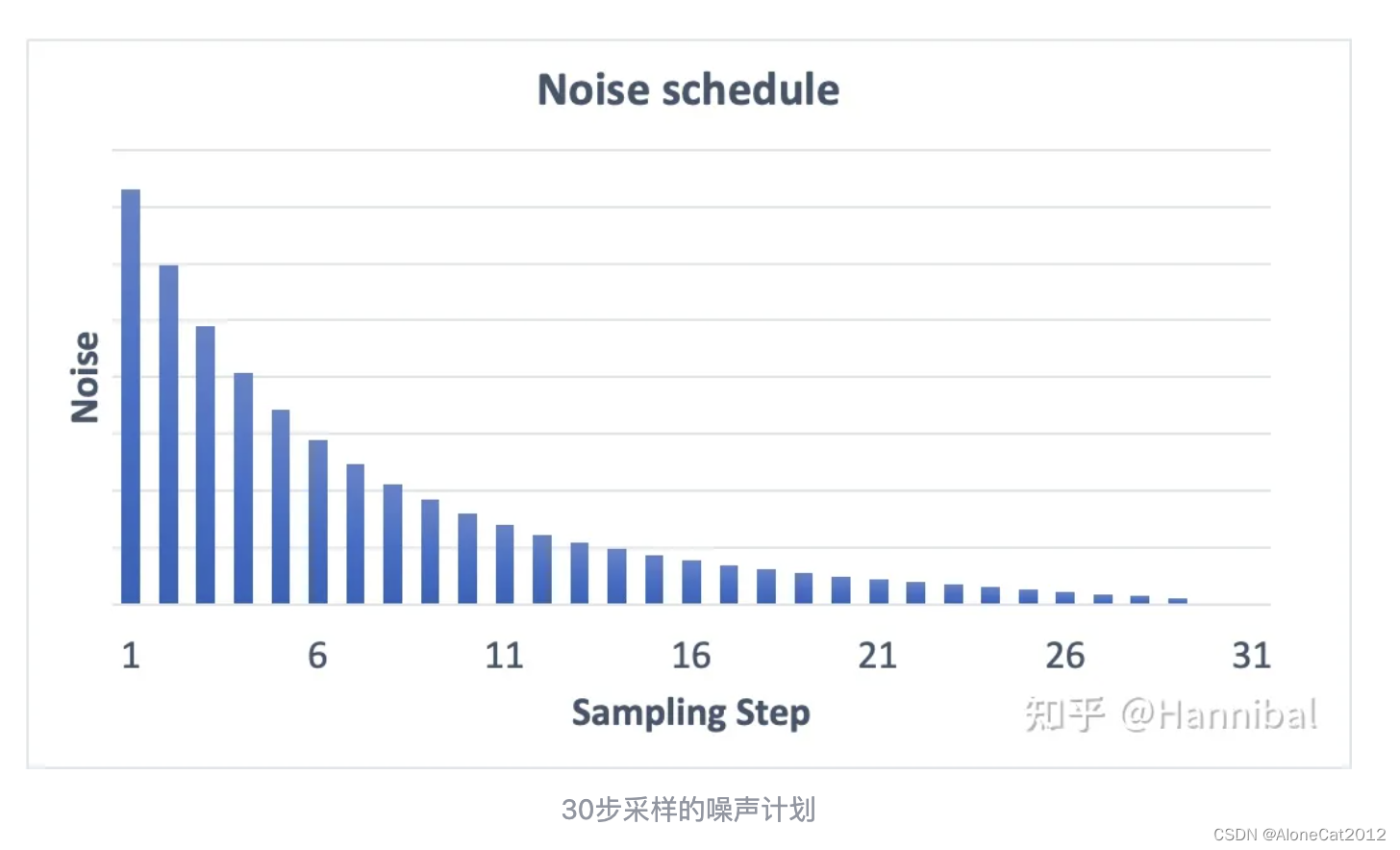
名字中带有karras的sampler是采用了karras论文中的噪声时间表(noise schedule)。它在前期噪声强度更高,而在末期噪声强度更低。
噪音计划表(Noise schedule)控制每个采样步骤的采样水平。整体噪声在第一步时最高,在最后一步逐步降低到零。(在每一步中,采样器会生成噪音水平与噪音计划表匹配的图像。增加采样步数,会缩小每一步的降噪幅度,有助于减少采样的截断误差。)
DDIM (Denoising Diffusion Implicit Model,去噪扩散隐式模型)和PLMS (Pseudo Linear Multi-Step method,伪线性多步法)是初始的1.0版本SD自带的采样器。
一般被认为是过时的而不再使用。
DPM系列
DPM (Diffusion probabilistic model solver,扩散概率模型求解器)是2022年发布的为扩散模型而设计的一系列采样器。
DPM++是DPM的改进版。
DPM2是二阶版本的DPM,更准确,但更慢。
DPM++SDE和DPM++SDE Karras有与祖先采样器相同的缺点,不会收敛,而且采样步数会显著影响图像内容。
DPM adaptive会自适应地改变采样步长,因而它不能保证在你所设定的步骤内完成采样任务,可能会很慢。
UniPC
UniPC (Unified Predictor-Corrector,统一预测-校正器)是2023年新发布的采样器,受到同名的常微分方程求解法思路的影响。可以在5-10个步骤中实现高质量图像生成。
k-diffusion
这个词并不指某一个采样器,它指的是Katherine Crowson的k-diffusion Github库和与之相关的采样器,正是这个库实现了karras2022年论文中的采样方法,基本上除了DDIM、PLMS、UniPC的其他采样器都部分衍生自k-diffusion。
针对所有采样器的输入和输出都是:
输入:
- 文本提示(Text Prompt):这是采样过程的关键输入之一。模型接收到一个自然语言描述作为条件约束,这个描述可以是用户想要生成图像的主题、风格、场景等具体信息。
- 随机噪声:在某些情况下,模型可能需要从一个随机分布中获取初始噪声图像作为起点。这个噪声图像随后经过扩散过程逐步转化为有意义的图像。
- 采样参数:包括采样的步数、步长、以及可能的其他超参数,这些控制着从随机状态到最终图像生成过程中噪声的去噪程度和速度。
输出
- 生成的图像:经过扩散模型反向传播的迭代过程后,最终得到的是一个与输入文本提示匹配的高分辨率、逼真的图像。这个图像应该反映了用户所提供的文字描述所蕴含的内容和细节。
- 中间态图像:在每次迭代过程中,模型都会产生一系列逐渐清晰化的图像,这些都是采样过程中的中间结果,展示了从噪声到目标图像的连续演化过程。
另外说点题外的,只是stable diffusion的采样需要求解常微分方程所以比较复杂,正常说的采样非常简单,介绍一个最简单的采样器
import numpy as np
# 均匀随机采样一个数,范围在0到1之间
random_sample = np.random.uniform(0, 1)
print(random_sample)
这个操作只是从0到1之间随机拿一个数,但就是一个采样器了,就是这样。