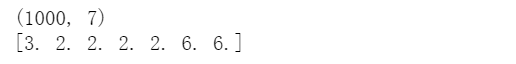来自：宋天龙《PYTHON数据分析与数据化运营》，以下内容比较简陋，方便日后翻阅。

1. python实现数据降维

数据降维的情况：
1.维度数量
2.建模是否需要保留原始维度，保留：特征选择；不保留：特征转化（PCA,LDA）
3.对模型的计算效率和时效性
降维的方式：特征选择，特征转换，特征组合

import numpy as np
from sklearn.tree import DecisionTreeClassifier# 决策树分类器，用于结合selectfrommodel提取特征
from sklearn import feature_selection
from sklearn.svm import SVC#支持向量机，用于结合RFE提取特征
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.preprocessing import PolynomialFeatures as plf#从多项式模型中提取特征
from sklearn.ensemble import GradientBoostingClassifier as GBDT#从GBDT中提取特征
from gplearn.genetic import SymbolicTransformer#从遗传基因中的符号方法中提取组合特征
from sklearn import datasets
# 读取数据文件
data = np.loadtxt('data1.txt')  # 读取文本数据文件
x, y = data[:, :-1], data[:, -1]  # 获得输入的x和目标变量y
print(x[:3])  # 打印输出x的前3条记录

2. 利用特征选择降维

1.使用SelectPercentile选择特征，设置选择总体30%的特征

selector_1 = feature_selection.SelectPercentile(percentile=30)#设置选择总体30%特征
sel_features1 = selector_1.fit_transform(x, y)  # 训练并转换数据
print(sel_features1.shape)  # 打印形状
print(sel_features1[:3])  # 打印前3条记录；保留了4-6-9列的数据

2.使用VarianceThreshold选择特征，只筛选方差大于1的特征

selector_2 = feature_selection.VarianceThreshold(1)#方差高于1的特征被选择下来
sel_features2 = selector_2.fit_transform(x)  # 训练并转换数据
print(sel_features2.shape)  # 打印形状
print(sel_features2[:3])  # 打印前3条记录，保留了1-3-4-5-7-8-9列的数据

3.RFE选择特征

# 使用RFE选择特征
model_svc = SVC(kernel="linear")
selector_3 = feature_selection.RFE(model_svc, 3)#保留3个得分最高的特征
sel_features3 = selector_3.fit_transform(x, y)  # 训练并转换数据
print(sel_features3.shape)  # 打印形状
print(sel_features3[:3])  # 打印前3条记录，保留了4-6-9列的数据

4.决策树

# 使用SelectFromModel选择特征
#我们指定基础模型器为决策树，不设置特征重要性的过滤阈值，因为我们事先不知道特征重要性的分布
model_tree = DecisionTreeClassifier(random_state=0)  # 建立分类决策树模型对象
selector_4 = feature_selection.SelectFromModel(model_tree)
sel_features4 = selector_4.fit_transform(x, y)  # 训练并转换数据
print(sel_features4.shape)  # 打印形状
print(sel_features4[:3])  # 打印前3条记录，保留了3-4-6列的数据

3. 利用转换降维

1.PCA降维

from sklearn.decomposition import PCA
model_lda = PCA(3)  # 建立PCA模型对象
model_lda.fit(x, y)  # 将数据集输入模型并训练
convert_features = model_lda.transform(x)  # 转换数据
print(convert_features.shape)  # 打印形状
print(model_lda.explained_variance_ratio_)  # 获得各成分解释方差占比
print(convert_features[:3])  # 

2.LDA考虑了标签的信息，使得变换后的特征也容易分类；PCA不考虑标签信息。

# 使用sklearn的LDA进行维度转换
model_lda = LDA()  # 建立LDA模型对象
model_lda.fit(x, y)  # 将数据集输入模型并训练
convert_features = model_lda.transform(x)  # 转换数据
print(convert_features.shape)  # 打印形状
print(model_lda.explained_variance_ratio_)  # 获得各成分解释方差占比
print(convert_features[:3])  # 打印前3条记录

4 .利用组合特征降维

1.基于树组合特征

# 使用sklearn的GBDT方法组合特征
model_gbdt = GBDT(n_estimators=7,max_depth=2)#将原来的10个特征组合成7个特征
model_gbdt.fit(x, y)
conbine_features = model_gbdt.apply(x)[:, :, 0]
print(conbine_features.shape)  # 打印形状
print(conbine_features[0])  # 打印第1条记录

2.从多项式模型中提取特征

# 使用sklearn的PolynomialFeatures方法组合特征
model_plf = plf(2)#参数表示多项式的度数
plf_features = model_plf.fit_transform(x)
print(plf_features.shape)  # 打印形状
print(plf_features[0])  # 打印第1条数据
print(model_plf.get_feature_names())#获取每个特征的名称

3.使用gplearn的genetic方法组合特征

raw_data = datasets.load_boston() # 加载数据集
x, y = raw_data.data, raw_data.target  # 分割形成x和y
print(x.shape) # 查看x的形状
print(x[0]) # 查看x的第一条数据
model_symbolic = SymbolicTransformer(n_components=5, generations=18,
                                     function_set=(
                                         'add', 'sub', 'mul', 'div', 'sqrt', 'log', 'abs', 'neg',
                                         'inv','max', 'min'),
                                     max_samples=0.9, metric='pearson',
                                     random_state=0, n_jobs=2)
model_symbolic.fit(x, y)  # 训练数据
symbolic_features = model_symbolic.transform(x)  # 转换数据
print(symbolic_features.shape)  # 打印形状
print(symbolic_features[0])  # 打印第1条数据
print(model_symbolic) # 输出公式