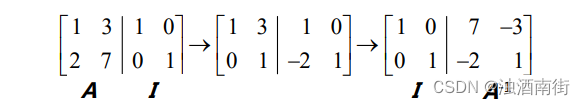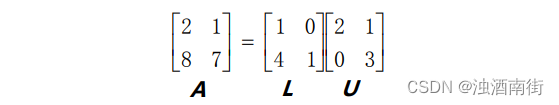1.系数矩阵

线性代数的基本问题就是解 n 元一次方程组。例如：二元一次方程组
$$\begin{array}{rl}& 2x-y=0\\ & -x+2y=3\end{array}$$
写成矩阵形式就是 :$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$
其中 A= $\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]$被称为系数矩阵（coefficient matrix）。 未知数向量通常记为 x= $\left[\begin{array}{c}x\\ y\end{array}\right]$,而等号右侧的向量记为 b。线性方程组简记为 Ax=b。

2.高斯消元法

消元法是计算机软件求解线形方程组所用的最常见的方法。任何情况下，只要是矩阵 A 可逆，均可以通过消元法求得 Ax=b 的解。
高斯消元法（Gauss elimination）就是通过对方程组中的某两个方程进行适当的数乘和加（jian）和（fa），以达到将某一未知数系数变为零，从而削减未知数个数的目的。

3.置换矩阵 Permutation

置换矩阵，是一种特殊的方阵，其中每行和每列只有一个元素为1，其他元素都为0。它表示了对向量或矩阵的行或列的置换操作。

置换矩阵的逆矩阵即为它的转置 $P^{-1}=P^T$。
置换矩阵 P 是通过对单位阵进行“行交换”得到的。对于 n x n 矩阵存在着 n！个置换矩阵。置换矩阵具有特殊性质$P^{-1}=P^T$ 即 $P^{T}P=I$。

4.逆矩阵 Inverse

逆矩阵，也称为反矩阵，是指一个方阵A的逆矩阵$A^{-1}$，它满足以下条件：
$A和A^{-1}$是方阵。
$A乘以A^{-}1等于单位矩阵I：A{A}^{-1}=A^{-1}A=I$。
$A^{-1}唯一存在，当且仅当A是可逆矩阵$。

如果矩阵 A 是方阵，若存在逆矩阵 $A^{-1}$，使得 $A^{-1}A=I=A{A}^{-1}$（左逆矩阵等于右逆矩阵）。我们称矩阵 A 可逆（invertible）或者矩阵 A 非奇异（nonsingular）。 反之，如果 A 为奇异（singular），则其没有逆矩阵。它的行列式为 0。另一个等价的说法是，A 为奇异阵，则方程 Ax=0 存在非零解 x。

5.高斯-若尔当消元法

高斯-约旦消元法是常用的求逆矩阵的方法，具体是在用高斯消元法的到上三角矩阵之后，按照若尔当的做法继续消元，用第一行
减去第二行的若干倍，最后原矩阵变为单位阵，这时右侧的矩阵即为逆矩阵。

6.矩阵的 LU 分解

LU分解是一种矩阵分解方法，它将一个矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积，即A=LU。其中，L是一个下三角矩阵，U是一个上三角矩阵。LU分解可以用于解决线性方程组和矩阵求逆等问题。

其中 U 为上三角阵（Upper triangular matrix），主元依次排列于它的对角线上，L 为下三角阵（Lower triangular matrix）。

7.三角矩阵

三角矩阵是指在矩阵中，一个方向上（通常是对角线以下或对角线以上）的元素全部为0的矩阵。根据对角线的位置，三角矩阵可以分为上三角矩阵和下三角矩阵两种类型。

下三角矩阵是指矩阵中对角线及其以上的元素全部为非零数，而对角线以下的元素全部为0的矩阵。$如：\left[\begin{array}{ccc}1& 0& 0\\ a& 2& 0\\ b& c& 3\end{array}\right]$

上三角矩阵是指矩阵中对角线及其以下的元素全部为非零数，而对角线以上的元素全部为0的矩阵。$如：\left[\begin{array}{ccc}1& a& b\\ 0& 2& c\\ 0& 0& 3\end{array}\right]$

三角矩阵通常是指方阵中的上三角矩阵和下三角矩阵，因此三角矩阵通常是方阵，尽管三角矩阵通常是方阵，但也存在非方阵的三角矩阵，例如下三角矩阵形如：$\left[\begin{array}{cccc}1& 0& 0& 0\\ a& 2& 0& 0\\ b& c& 3& 0\end{array}\right]$

8.正定矩阵

若矩阵 A 满足对任意向量 x≠0 均有 $x^{T}Ax$>0，则称矩阵为正定矩阵，可以通过特征值、主元和行列式的办法来判断矩阵的正定性。
正定矩阵 A 是对称矩阵,(是对称矩阵，一定是方阵),它的逆矩阵 $A^{-1}$也是正定矩阵，逆矩阵的特征值是原矩阵的倒数，因此也都是正数。
给定一个 2 x 2 矩阵，有四个途径判定矩阵是否正定矩阵：
1） 特征值：${\lambda }_1>0，{\lambda }_2>0$
2） 行列式（所有子行列式）：$a>0，ac-b^2>0$
3） 主元：$a>0，(ac-b2)/a>0$
4） 表达式 $x^{T}Ax>0$（x=0 除外）。通常这就是正定的定义，而前三条是用来验证正定性的条件。

$如A=\left[\begin{array}{cc}2& 6\\ 6& 20\end{array}\right]$ ,就是一个正定矩阵；

9.对称矩阵

对称矩阵是指矩阵A的转置矩阵等于矩阵A本身，即 $A=A^T$。对称矩阵一定是方阵，在对称矩阵中，对于矩阵中的每个元素A(i,j)，其与A(j,i)相等。因此，对称矩阵中只需要存储对角线上的元素和对角线以下的元素，就可以完全描述整个矩阵。

对称矩阵具有以下性质：

1. 对称矩阵的特征值都是实数。
2. 对称矩阵的特征向量可以正交化，即任意两个特征向量之间的内积为0。
3. 对称矩阵可以通过正交对角化来对角化，即可以找到一组正交矩阵，使得对称矩阵在这组正交矩阵的相似变换下变成一个对角矩阵。

10.奇异阵

奇异矩阵和奇异阵是一个概念，指的是行列式为零的矩阵，也称为非满秩矩阵。行列式是矩阵的一个标量值，表示矩阵中各行各列元素的乘积之和。如果一个矩阵的行列式为零，那么它就是奇异矩阵或奇异阵，否则它就是非奇异矩阵或非奇异阵。

奇异矩阵和奇异阵具有以下特点：

1. 奇异矩阵的秩小于矩阵的行数和列数，因为矩阵的秩等于矩阵的最大线性无关行数或列数，如果矩阵的行列式为零，那么它的最大线性无关行数或列数就小于矩阵的行数或列数。

2. 奇异矩阵的逆矩阵不存在，因为矩阵的逆矩阵是指使得矩阵与其逆矩阵相乘得到单位矩阵的矩阵，如果矩阵的行列式为零，那么它就没有逆矩阵。

11.向量空间

向量空间，也称为线性空间，是指一个非空集合V，其中定义了两种运算：向量的加法和标量与向量的乘法，同时满足以下八个条件：
向量的加法满足交换律和结合律。

1. 存在一个零向量，使得对于任意向量v，v+0=v。
2. 对于每个向量v，存在一个相反向量-u，使得v+u=0。
3. 标量与向量的乘法满足分配律和结合律。
4. 1是标量乘法的单位元。
5. 标量乘法满足结合律，即 (ab)v=a(bv)。
6. 标量乘法满足分配律，即 (a+b)v=av+b*v。
7. 标量乘法与向量的加法满足分配律，即 a*(u+v)=au+av。

$R^2$即为向量空间，它是具有两个实数分量的所有向量（二维实向量）的集合。

所有向量空间必然包含零向量，因为任何向量数乘 0 或者加上反向量都会得到零向量，而因为向量空间对线性运算封闭，所以零向量必属于向量空间。

$R^3$是向量空间，它是具有三个实数分量的所有向量的集合。
$R^n$是向量空间，它是具有 n 个实数分量的所有向量的集合。
反例：$R^2$中的第一象限则不是一个向量空间。

12.子空间

包含于向量空间之内的一个向量空间称为原向量空间的一个子空间。

R2的子空间包括：
• R2空间本身
• 过原点的一条直线（这是 R2空间中的一条直线，与 R1空间有区别）
• 原点 仅包含 0 向量 Z

R3的子空间包括：
• R3空间本身 3 维
• 过原点的一个平面 2 维
• 过原点的一条直线 1 维
• 原点 仅包含 0 向量 Z

13. 列空间

列空间，也称为向量空间的列空间或图像空间，是指一个矩阵A中所有列向量的张成空间，用C(A)表示。即列空间是由矩阵A的所有列向量所张成的向量空间。

列空间具有以下性质：

1. 列空间的维数等于矩阵A的列数。
2. 列空间的基向量可以通过对矩阵A进行列变换得到。
3. 列空间的任意向量都可以表示为矩阵A列向量的线性组合。

14.零空间

零空间，也称为零化空间，是指一个线性变换的所有零点向量所组成的向量空间。在数学中，一个线性变换T将向量空间V映射到向量空间W，如果T(x)=0，则向量x属于T的零空间，用N(T)表示。

零空间具有以下性质：

1. 零空间的维数等于线性变换的自由变量的个数。
2. 零空间的基向量可以通过对线性变换的矩阵进行初等行变换得到。
3. 零空间的任意向量都可以表示为零空间的基向量的线性组合。

矩阵 A 的零空间 N(A)是指满足 Ax=0 的所有解的集合。对于 m x n 矩阵，列空间为 $R^m$的子空间，零空间为$R^n$空间的子空间。

15.矩阵的秩

矩阵的秩是指一个矩阵中非零的行向量或列向量的最大线性无关组数。简单来说，就是矩阵中所包含的最大的线性无关行或列的数量。记为r(A)。
具体来说，可以通过高斯消元法或矩阵的初等变换来求解矩阵的秩。对于一个m行n列的矩阵A，可以将其进行行变换或列变换，得到一个行阶梯形矩阵或列阶梯形矩阵，从而可以得到矩阵的秩。行阶梯形矩阵和列阶梯形矩阵都具有相同的秩，且秩等于它们中非零行或列的数量。

矩阵的秩在线性代数和矩阵论中具有重要的应用，例如：

1. 矩阵的秩可以用来判断矩阵是否可逆，如果矩阵的秩等于其行数或列数，则矩阵是可逆矩阵。
2. 矩阵的秩可以用来判断矩阵的行空间和列空间的维数，如果矩阵的秩为r，则它的行空间和列空间的维数都为r。
3. 矩阵的秩可以用来求解线性方程组的解的个数，如果矩阵的秩等于未知量的个数，则线性方程组有唯一解，否则有无穷多个解。

总之，矩阵的秩是矩阵论和线性代数中一个非常重要的概念，它可以用来描述矩阵的各种性质和特征。

矩阵的秩等于矩阵的主元数。如果 m x n 矩阵的秩为 r，则必有 r≤m且r≤n。
讨论满秩（full rank）的情形：
• 列满秩：r=n。每列都有主元，x 的每一个分量都是主变量，没有自由变量。零空间 N(A)之内只有零向量。方程无解或者有唯一解 xp。

• 行满秩：r=m。每行都有主元，无论 b 取何值，方程 Ax=b 都有解。主变量 r 个，自由变量 n-r 个。

• 满秩 r=m=n，矩阵可逆。零空间只有零向量，无论 b 取何值，方程 Ax=b 都有唯一解。

16.线性无关

若$c_1{x}_1+c_2{x}_2+\dots \dots +c_n{x}_n=0$ 仅在 $c_1=c_2=\dots \dots =c_n=0$ 时才成立，则称向量 $x_1，x_2\dots \dots x_n$是线性无关的。若这些向量作为列向量构成矩阵 A，则方程 Ax=0 只有零解 x=0，或称矩阵 A 的零空间只有零向量。换而言之，若存在非零向量 c，使得Ac=0，则这个矩阵 A 的列向量线性相关。

如果矩阵 A 的列向量为线性无关，则 A 所有的列均为主元列，没有自由列，矩阵的秩为 n。若 A 的列向量为线性相关，则矩阵的秩小于 n，并且存在自由列。

持续更进中！！！！