本文通过一个虚拟的数据集,对之前的内容做一个回顾。
本文涉及的绘图对象详见:
散点图绘制传送门
条形图、直方图绘制传送门
箱线图绘制传送门
文末多子图、分类边界的绘制详见:
子图绘制传送门
等高面图绘制传送门
文章目录
本文的运行环境为 jupyter notebook
python版本为3.7
本文所用到的库包括
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# 所有字体大小设置为15号
plt.rcParams['xtick.labelsize'] = 15
plt.rcParams['ytick.labelsize'] = 15
plt.rcParams['legend.fontsize'] = 15
plt.rcParams['axes.labelsize'] = 15
plt.rcParams['axes.titlesize'] = 15
构造数据集
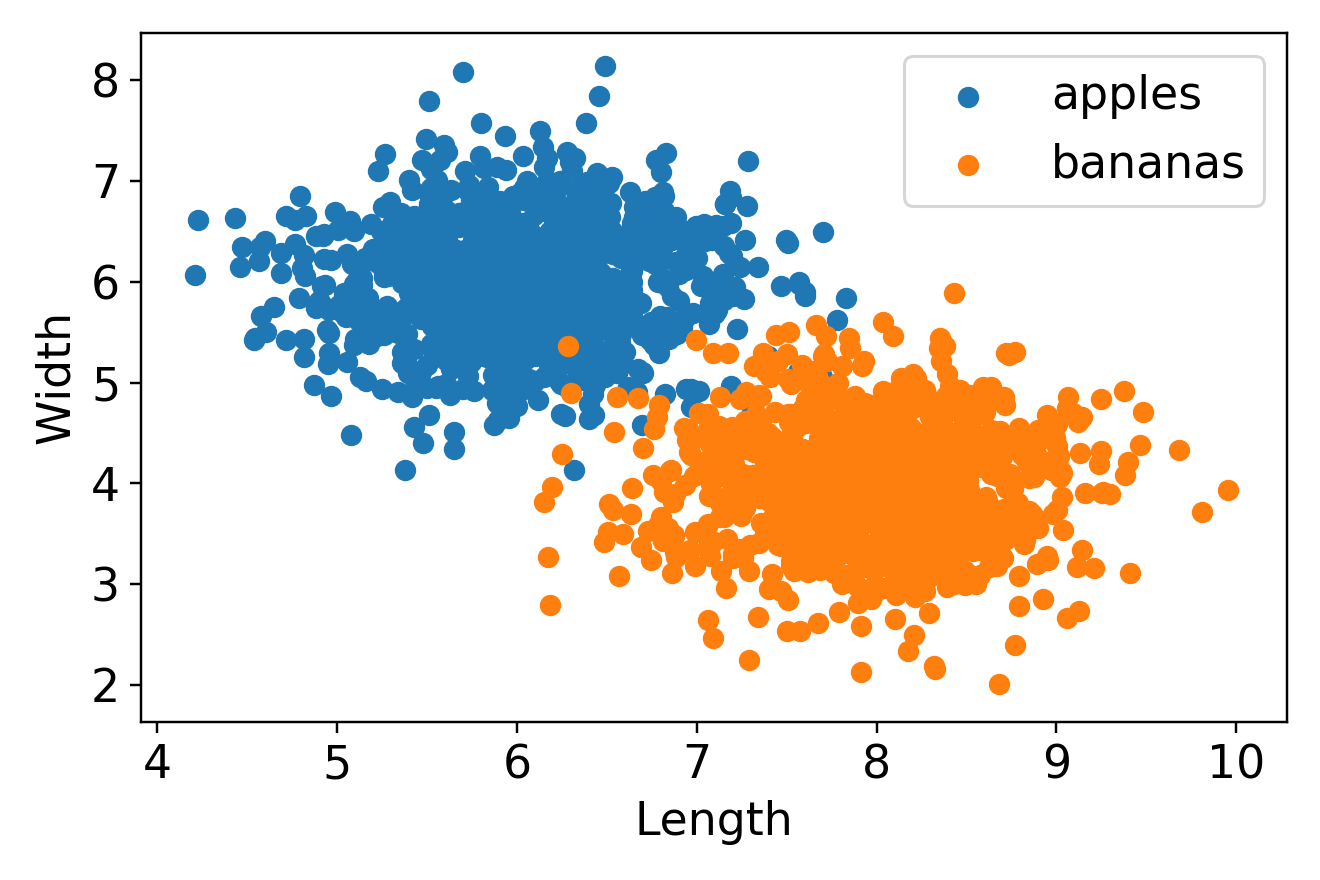
如下图所示,本文构建的数据集包含两种水果的两个特征,特征1为水果截面图的长度,特征2为水果截面图的宽度。
构建数据集代码如下:
以8为中心值,0.6为标准偏差的正态分布数据构造香蕉长度特征。
以4为中心值,0.6为标准偏差的正态分布数据构造香蕉宽度特征,
相比香蕉而言,苹果长宽比较为均衡。
以6为中心值,0.6为标准偏差的正态分布数据构造苹果长度特征,
以6为中心值,0.6为标准偏差的正态分布数据构造苹果宽度特征,
共生成3个pandas数据集,分别为香蕉(bananas),苹果(apples)和包含了香蕉和苹果的水果(fruits),包含香蕉和苹果各1000个,每个数据集都包含一个分类列(class),香蕉的分类用整型数字 0 表示,苹果用数字 1 表示。
np.random.seed(121)
N = 1000
std = 0.6
bananas = pd.DataFrame({
'length': np.random.normal(8, std, N),
'width': np.random.normal(4, std, N),
'class': np.zeros(N, dtype='int')}
)
apples = pd.DataFrame({
'length': np.random.normal(6, std, N),
'width': np.random.normal(6, std, N),
'class': np.ones(N, dtype='int')}
)
fruits = pd.concat([bananas, apples])
数据分布图
散点图
将长、宽特征映射到散点图观察两类水果数据分布情况。(代码注释部分传送门未涉及,对于数据框类数据集的赋值,建议注释部分的传参方式,以增加可读性)
plt.scatter(x=apples['length'], y=apples['width'], label='apples')
plt.scatter(x=bananas['length'], y=bananas['width'], label='bananas')
plt.legend()
plt.xlabel('Length')
plt.ylabel('Width')
######### 以上代码等价以下代码。对于数据框(pandas对象)可通过列名直接赋值 #########
# plt.scatter(x='length', y='width', data=apples, label='apples')
# plt.scatter(x='length', y='width', data=bananas, label='bananas')
# plt.legend()
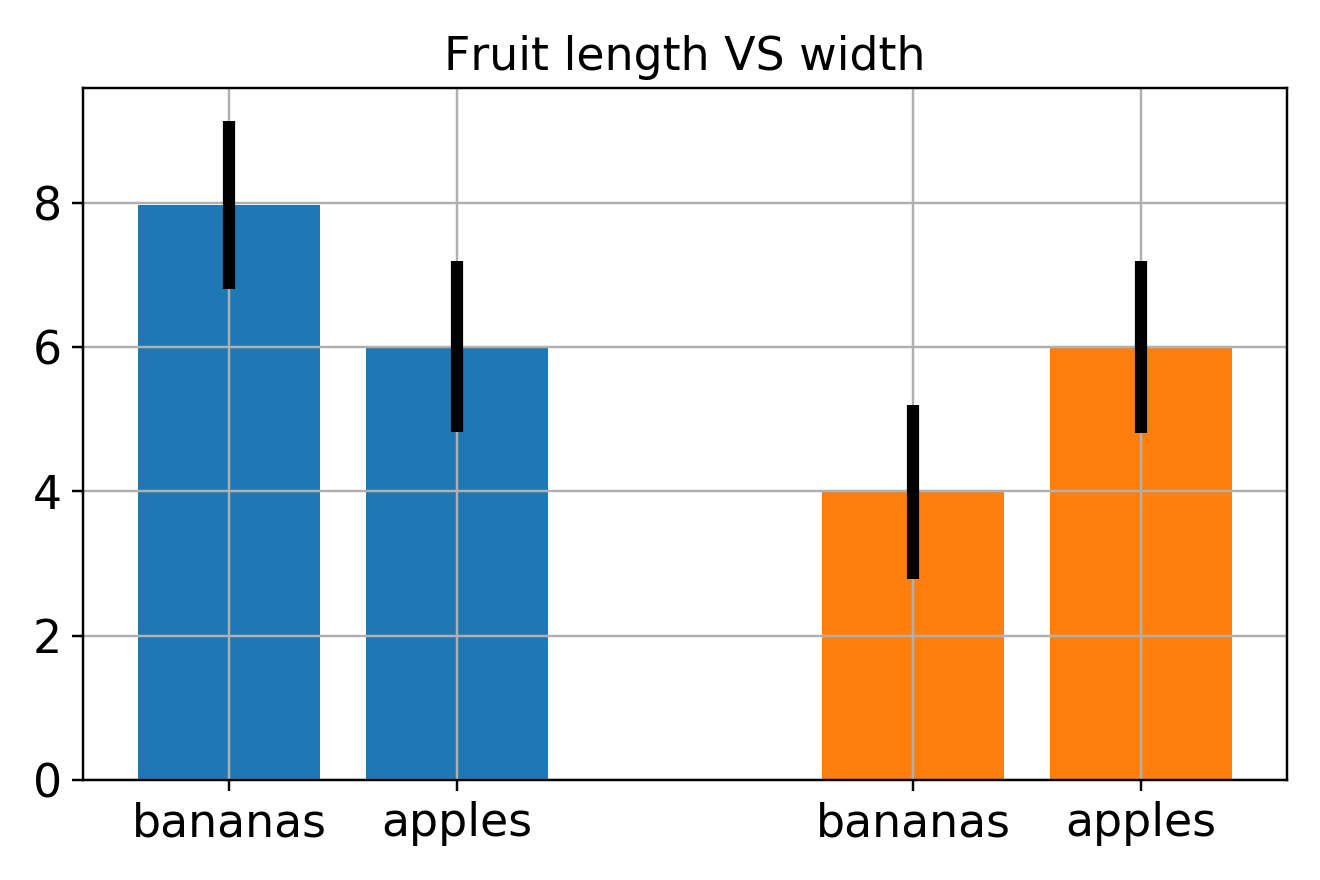
带误差棒的条形图
以2倍标准偏差绘制误差线,分别比较两类水果的长度和宽度特征,显而易见的,均值上,香蕉比苹果长,但是苹果比香蕉宽。
labels = ['bananas', 'apples', 'bananas', 'apples']
x = [1, 1.5, 2.5, 3.0]
height = [fruits.loc[fruits['class'] == 0, 'length'].mean(),
fruits.loc[fruits['class'] == 1, 'length'].mean(),
fruits.loc[fruits['class'] == 0, 'width'].mean(),
fruits.loc[fruits['class'] == 1, 'width'].mean()]
yerr = [2*fruits.loc[fruits['class'] == 0, 'length'].std(),
2*fruits.loc[fruits['class'] == 1, 'length'].std(),
2*fruits.loc[fruits['class'] == 0, 'width'].std(),
2*fruits.loc[fruits['class'] == 1, 'width'].std()]
color = ['tab:blue', 'tab:blue', 'tab:orange', 'tab:orange']
plt.bar(x=x,
height=height,
color=color,
width=0.4,
error_kw={'lw': 4},
yerr=yerr)
plt.xticks(ticks=x, labels=labels)
plt.title('Fruit length VS width')
plt.grid()
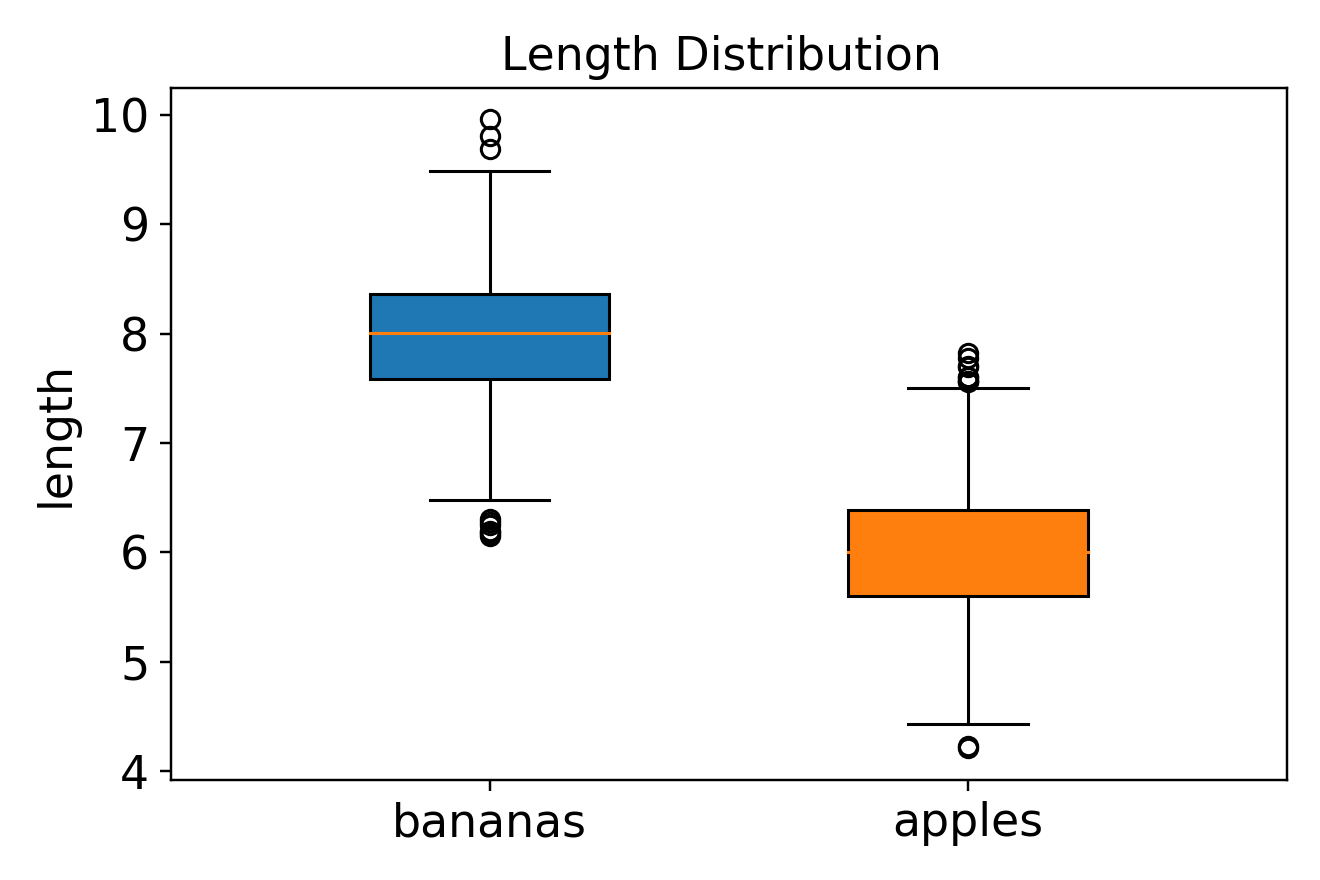
箱线图
从箱线图可以看出,两类水果在长度特征上,分布差异明显。
fea = 'length'
plt.boxplot(x=fea, data=fruits.loc[fruits['class'] == 0],
patch_artist=True, boxprops={'facecolor': 'tab:blue'},
positions=[0], labels=['bananas'], widths=[0.15])
plt.boxplot(x=fea, data=fruits.loc[fruits['class'] == 1],
patch_artist=True, boxprops={'facecolor': 'tab:orange'},
positions=[0.3], labels=['apples'], widths=[0.15])
plt.ylabel('length')
plt.xlim(-0.2, 0.5)
plt.title('Length Distribution ')
直方图
另一种有效展示特征分布的图形为直方图,从下图可以看出,两类水果宽度呈现两种不同分布,但有部分区域存在重叠。(大香蕉和小苹果)
fea = 'width'
plt.hist(x=fea, data=fruits.loc[fruits['class'] == 0],
bins=30, density=True, color='tab:blue', label='bananas',)
plt.hist(x=fea, data=fruits.loc[fruits['class'] == 1],
bins=30, density=True, color='tab:orange', label='apples', alpha=0.8)
plt.legend(frameon=False)
plt.title('Width Distribution ')
plt.xlabel('Width')
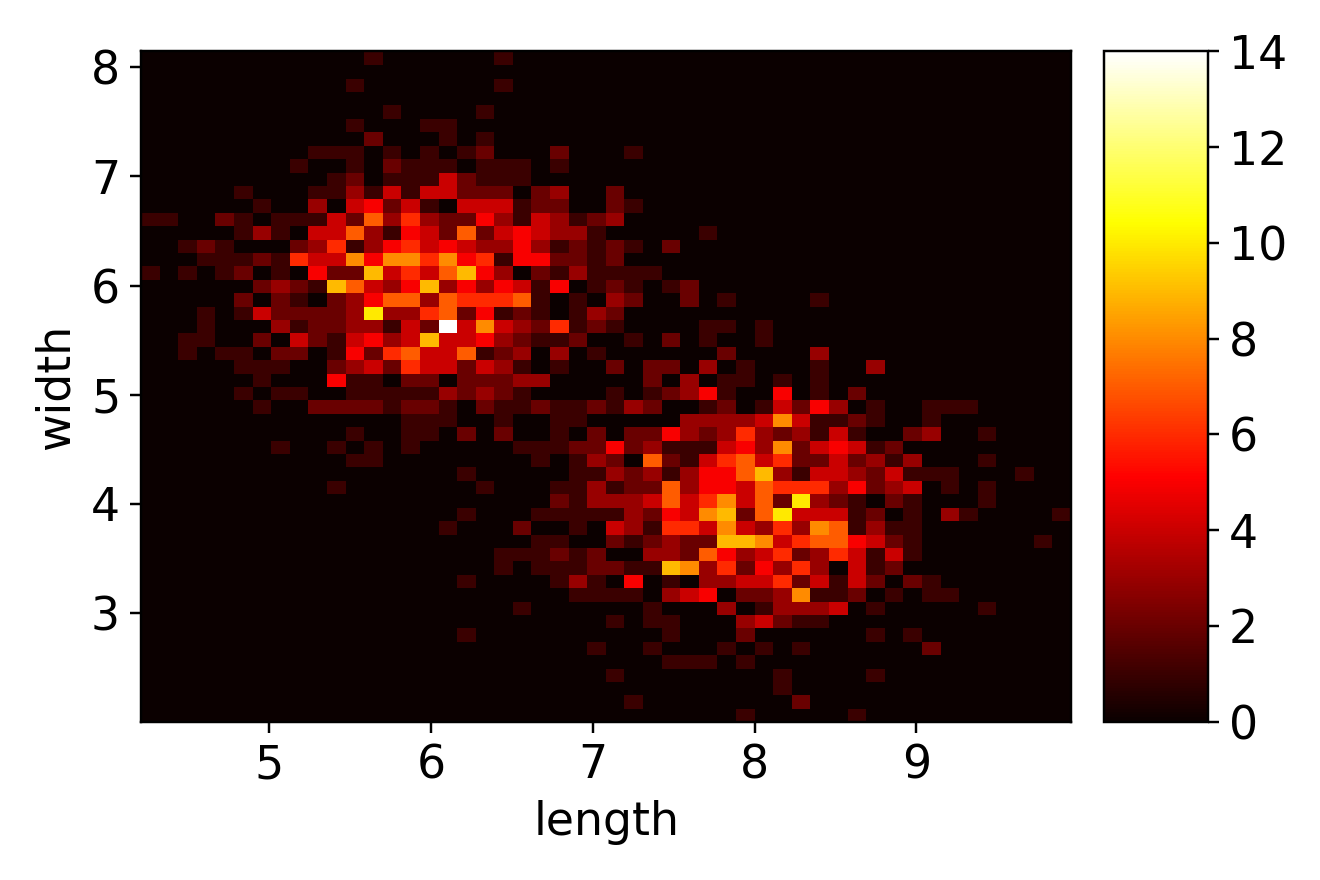
联合分布直方图
plt.hist2d(ax.hist2d)接口可以更形象地描述两个特征的联合分布情况,黄色部分表示该区域的样本密度大,黑色部分表示该区域的样本密度小。
fig, (ax, cax) = plt.subplots(1, 2, gridspec_kw={'width_ratios': [0.9, 0.1]})
_, _, _, mappable = ax.hist2d(
x='length', y='width', bins=50, data=fruits, cmap=plt.cm.hot)
ax.set_xlabel('length')
ax.set_ylabel('width')
plt.colorbar(mappable=mappable, cax=cax, ax=ax)
想象这样一个场景:香蕉和苹果一个个地以固定时间间隔经过传送带,传送带上有一个工业摄像头,该摄像头经图像分析算法可以获得前文所述的水果截面长度和宽度的数据,那么,如果通过一个更好的特征识别出该水果是香蕉,还是苹果? 完成识别后到下一个节点,可通过万向轮将不同种类的水果传输到不同的收集框。
特征生成与选择
长宽比
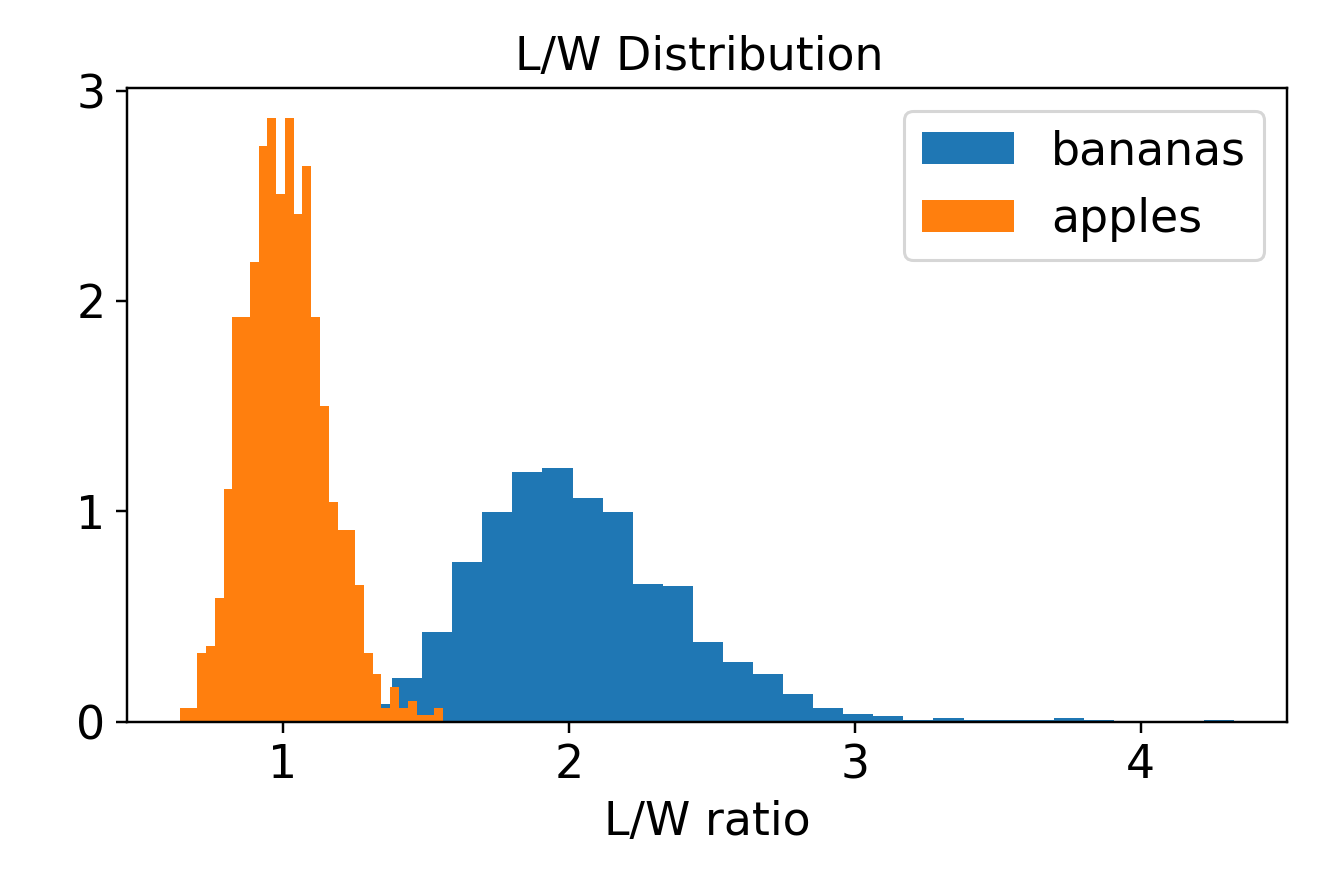
将水果的长度除以水果的宽度,可以获得水果的长宽比,两类水果的长宽比分布如下:
fea = 'L/W'
fruits[fea] = fruits['length']/fruits['width']
plt.hist(x=fea, data=fruits.loc[fruits['class'] == 0],
bins=30, density=True, color='tab:blue', label='bananas',)
plt.hist(x=fea, data=fruits.loc[fruits['class'] == 1],
bins=30, density=True, color='tab:orange', label='apples',)
plt.legend()
plt.title('L/W Distribution ')
plt.xlabel('L/W ratio')
从图中可以看出,长宽比,这个特征很好地将香蕉和水果的分布分离开,重叠面积很小。
毕竟,经验上我们知道香蕉是瘦长的而苹果是圆的,该特征较高程度地提炼出两种水果的主要差异。
面积
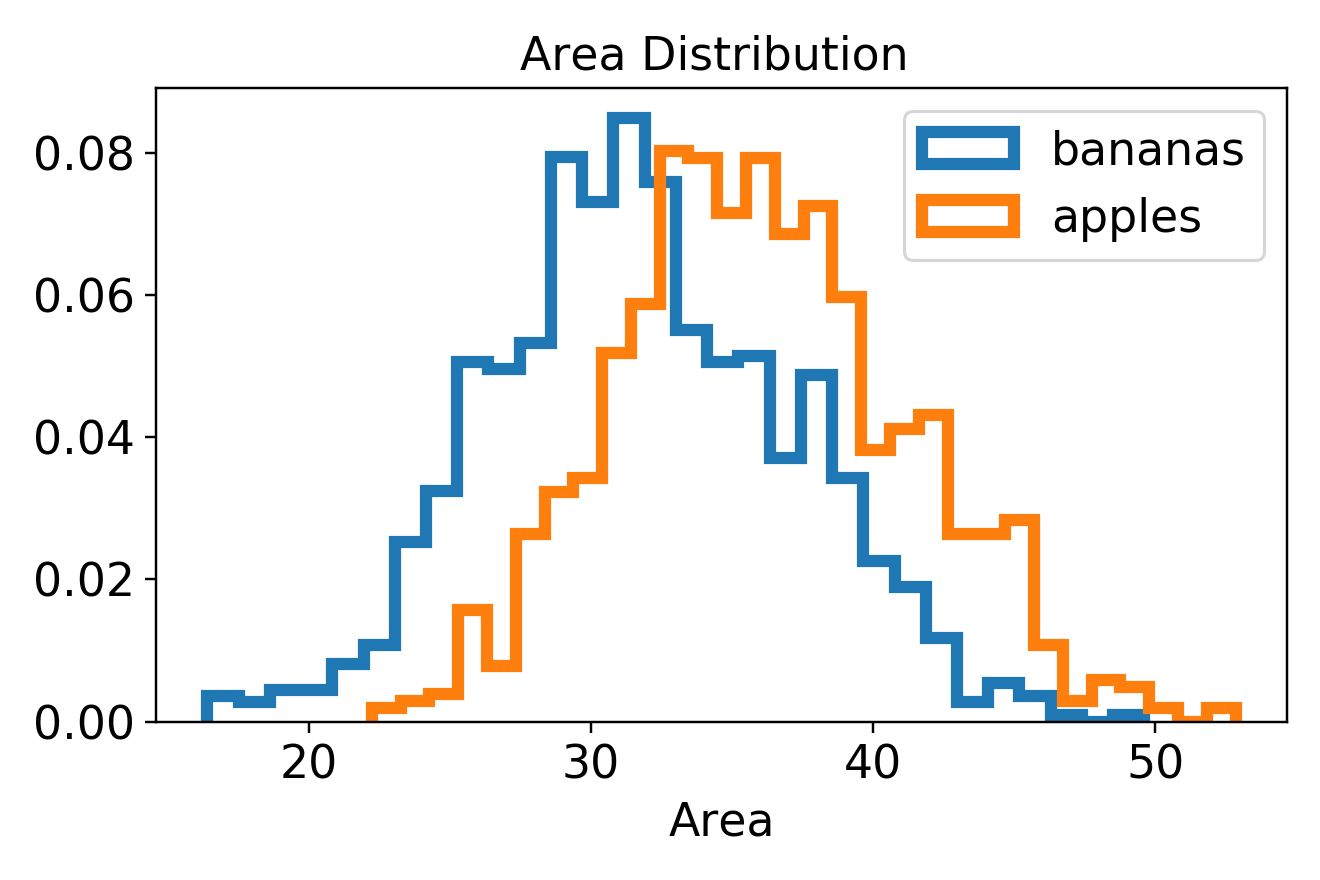
将水果的长度乘以水果的宽度,可以获得水果的面积,两类水果的面积分布如下:
fea = 'area'
fruits[fea] = fruits['length']*fruits['width']
plt.hist(x=fea, data=fruits.loc[fruits['class'] == 0], histtype='step', lw=4,
bins=30, density=True, color='tab:blue', label='bananas')
plt.hist(x=fea, data=fruits.loc[fruits['class'] == 1], histtype='step', lw=4,
bins=30, density=True, color='tab:orange', label='apples')
plt.title('Area Distribution ')
plt.legend()
plt.xlabel('Area')
周长
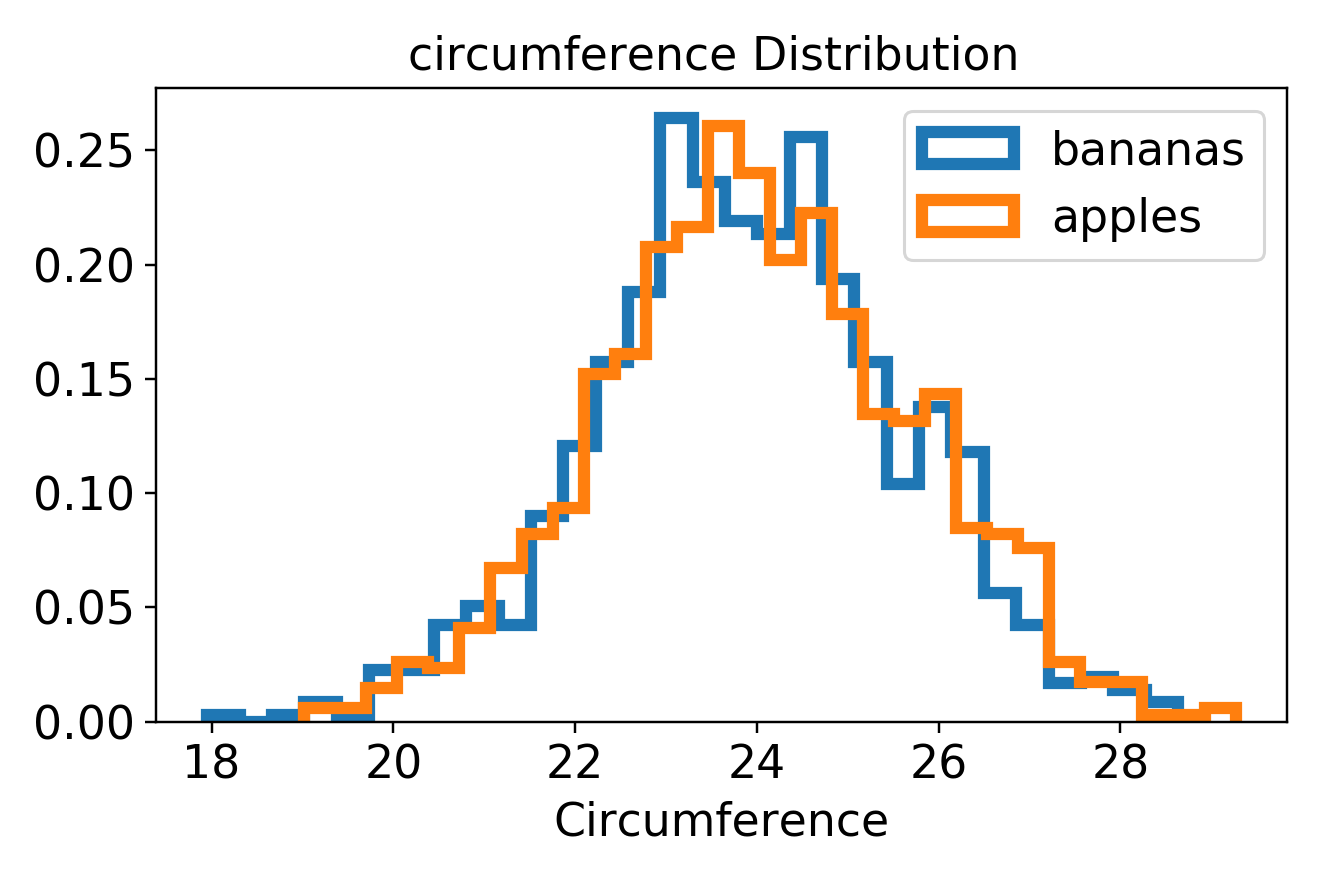
将水果的长度加上水果的宽度,再乘以2,可以获得水果的周长,两类水果的周长分布如下:
fea = 'circumference'
fruits[fea] = 2*(fruits['length']+fruits['width'])
plt.hist(x=fea, data=fruits.loc[fruits['class'] == 0], histtype='step', lw=4,
bins=30, density=True, color='tab:blue', label='bananas')
plt.hist(x=fea, data=fruits.loc[fruits['class'] == 1], histtype='step', lw=4,
bins=30, density=True, color='tab:orange', label='apples')
plt.title('circumference Distribution ')
plt.legend()
plt.xlabel('Circumference')
从面积、周长分布图可以看出,两类水果的重叠面积非常大,说明用这两个特征分类香蕉和苹果大概率会错分。
显著性检验
可以用scipy库的stats.ttest_ind接口对两类水果在长宽比、面积、周长三个特征上做独立t检验,t检验拒绝了长宽比、面积上两类水果中心值相同的原假设。
from scipy import stats
fea = 'L/W'
fruits[fea] = fruits['length']/fruits['width']
stats.ttest_ind(fruits.loc[fruits['class'] == 0, fea],
fruits.loc[fruits['class'] == 1, fea])
输出
Ttest_indResult(statistic=82.438425661083, pvalue=0.0)
fea = 'area'
fruits[fea] = fruits['length']*fruits['width']
stats.ttest_ind(fruits.loc[fruits['class'] == 0, fea],
fruits.loc[fruits['class'] == 1, fea])
输出
Ttest_indResult(statistic=-18.33979554877528, pvalue=1.4737736564093967e-69)
fea = 'circumference'
fruits[fea] = 2*(fruits['length']+fruits['width'])
stats.ttest_ind(fruits.loc[fruits['class'] == 0, fea],
fruits.loc[fruits['class'] == 1, fea])
输出
Ttest_indResult(statistic=-1.3170522756675043, pvalue=0.1879721312693096)
t检验结果汇总表
| 特征 | 特征 | t-统计量 | p-value | reject |
|---|---|---|---|---|
| 长宽比 | L/W | 82.44 | 0.0 | True |
| 面积 | Area | -18.34 | 1.47e-69 | True |
| 周长 | Circumference | -1.32 | 0.19 (>0.05) | False |
聚类算法训练过程可视化
聚类分析又称群分析,是机器学习的一个重要算法。以下过程演示了用K-MEANS算法对两类水果聚类的过程。
定义函数-计算距离
各样本到簇心的距离,采用欧式距离,distance_L函数实现了各样本与簇心距离的计算。
def distance_L(fea_1, fea_2, center_x, center_y, data):
x_x = np.power(data[fea_1]-center_x, 2) # (x-cx)^2
y_y = np.power(data[fea_2]-center_y, 2) # (y-cy)^2
return np.array(np.sqrt(x_x+y_y))
定义函数-训练簇心
train_centers函数定义了模型训练过程,通过传入上一次得到的簇心,计算下一次的簇心。
def train_centers(fea_1, fea_2, centers, data):
# 上一个迭代次获得的簇心
(center1_x, center1_y), (center2_x, center2_y) = centers
# 分别计算与簇心1,和簇心2的欧式距离
distance_1 = distance_L(fea_1, fea_2, center1_x, center1_y, data)
distance_2 = distance_L(fea_1, fea_2, center2_x, center2_y, data)
# 与 center1 欧氏距离较近的数据点,他们的均值为新簇心
center1_x = data.loc[distance_1 < distance_2, fea_1].mean()
center1_y = data.loc[distance_1 < distance_2, fea_2].mean()
# 与 center2 欧氏距离较近的数据点,他们的均值为新簇心
center2_x = data.loc[distance_1 > distance_2, fea_1].mean()
center2_y = data.loc[distance_1 > distance_2, fea_2].mean()
return (center1_x, center1_y), (center2_x, center2_y)
# 测试
train_centers('length', 'width', centers=((3, 3), (8, 8)), data=fruits)
# ((3, 3), (8, 8)) 经一次训练后变为 ((6.286898045335904, 4.2832890208506464), (7.082150034373463, 5.088522425327138))
输出
((6.286898045335904, 4.2832890208506464),
(7.082150034373463, 5.088522425327138))
测试代码展示了簇心经训练由(3, 3), (8, 8)变为((6.286898045335904, 4.2832890208506464), (7.082150034373463, 5.088522425327138))。
定义函数预测分类
pred_centers接口实现了由簇心预测传入新样本应属于哪一类别。
def pred_centers(x, y, centers):
(center1_x, center1_y), (center2_x, center2_y) = centers
# 需要预测的x,y与簇心的距离
d1 = np.sqrt(np.power(x-center1_x, 2)+np.power(y-center1_y, 2))
d2 = np.sqrt(np.power(x-center2_x, 2)+np.power(y-center2_y, 2))
# 若距离center1簇心的距离小于center2,则为0,否则为1,此处将bool直接转为int
pred_classes = np.array(d1 < d2, dtype='int')
return pred_classes
# 测试
x = np.array([[1, 1, 1], [5, 5, 5], [10, 10, 10]])
y = np.array([[1, 5, 10], [1, 5, 10], [1, 5, 10]])
pred_centers(x, y, [[3, 6], [9, 5]])
输出
array([[1, 1, 1],
[1, 1, 1],
[0, 0, 0]])
开始训练
训练开始时,先随机生成两个簇心(因为有两类水果),随后训练5次,每次训练得到的簇心均保存至centers_all列表,输出部分打印了初始簇心及训练第一次得到的簇心。
np.random.seed(122)
fea_1, fea_2 = 'length', 'width'
epochs = 5
centers = np.random.randint(low=3, high=10, size=(2, 2)) # 随机初始化香蕉和苹果的簇心
centers_all = [centers] # 保存所有迭代次数的簇心
for i in range(epochs):
centers = train_centers(fea_1, fea_2, centers, data=fruits)
centers_all.append(centers)
centers_all[:2]
输出
[array([[5, 5],
[9, 7]]),
((6.5143691190390625, 5.177757867221544),
(8.199241667306879, 4.528661649079994))]
绘制某一步的簇心及预测边界
将训练1次的簇心及其分类效果可视化如下,簇心已从初始的随机值移动至较接近两类水果数据集的中心位置。
epoch = 1
# 绘制水果的原始数据图
plt.scatter(x=apples['length'], y=apples['width'], label='apples', s=20)
plt.scatter(x=bananas['length'], y=bananas['width'], label='bananas', s=20)
# 绘制簇心
(center1_x, center1_y), (center2_x, center2_y) = centers_all[epoch]
plt.scatter(center1_x, center1_y, marker='^', s=300, c='r')
plt.scatter(center2_x, center2_y, marker='v', s=300, c='r')
plt.xlim(4, 10)
plt.ylim(1, 9)
# 绘制分类边界
x = np.linspace(4, 10, 100)
y = np.linspace(1, 9, 100)
X, Y = np.meshgrid(x, y)
Z = pred_centers(X, Y, centers_all[epoch])
plt.contourf(X, Y, Z, cmap=plt.cm.hot, alpha=0.3)
plt.xlabel('Length')
plt.ylabel('Width')
# 标题图例
plt.title('Cluster centers after train epoch: %d' % epoch)
plt.legend()
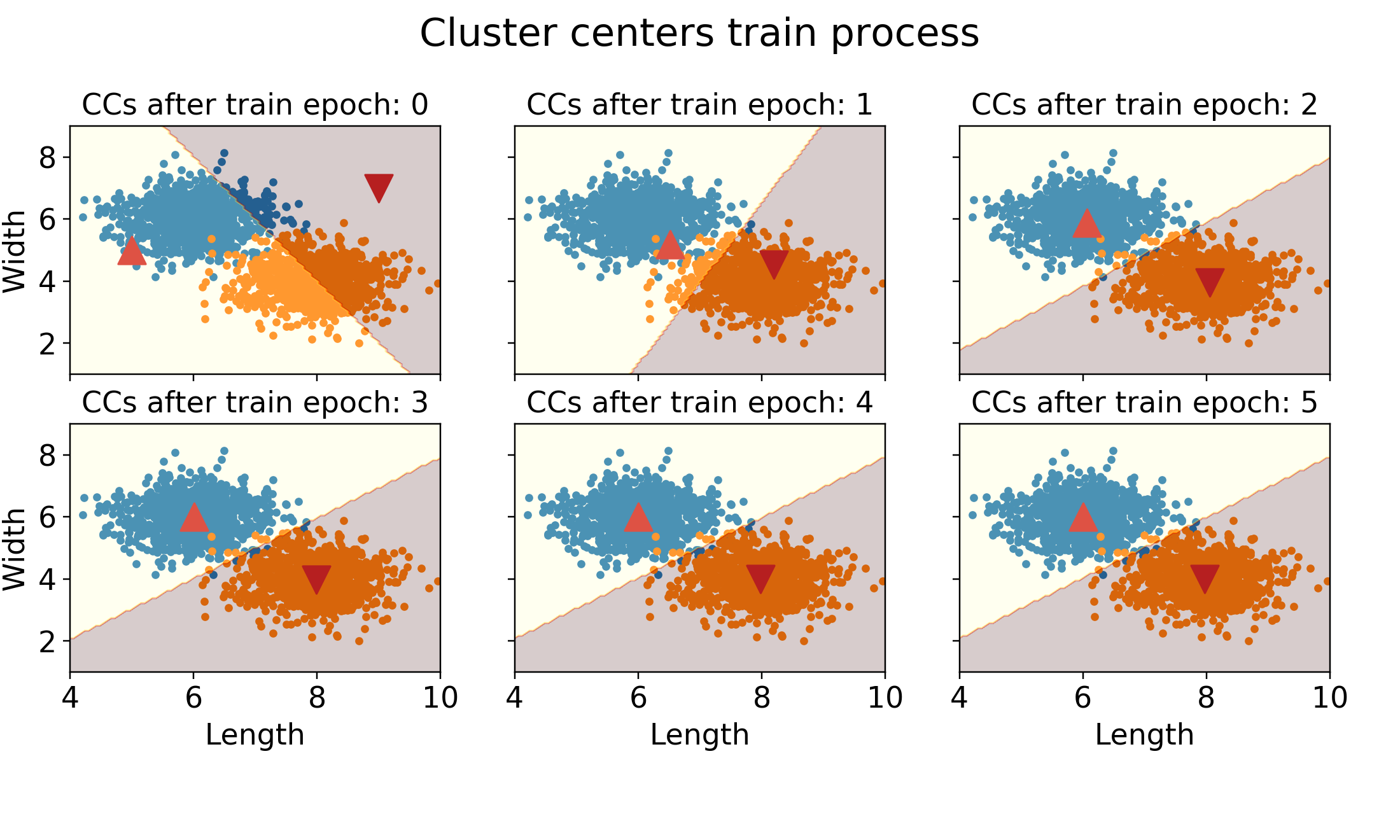
绘制训练过程的簇心及分类边界
以下过程绘制了各迭代次数下,簇心的移动及当前簇心的分类边界,从图中可以看出迭代至第3次,模型已能很好地将香蕉和水果分开,两个簇心(5次训练后得到的簇心((6.000, 6.001),
(7.973, 3.989)))与我们前文构造的((6,6),(8,4))较为一致。
# 将6次迭代过程分类边界和簇心可视化
fig, axs = plt.subplots(2, 3, sharex=True, sharey=True, figsize=(10, 6))
fig.suptitle('Cluster centers train process',fontsize=20,va='top')
axs = axs.ravel()
for epoch, ax in enumerate(axs):
ax.scatter(x=apples['length'], y=apples['width'], label='apples', s=10)
ax.scatter(x=bananas['length'], y=bananas['width'], label='bananas', s=10)
(center1_x, center1_y), (center2_x, center2_y) = centers_all[epoch]
ax.scatter(center1_x, center1_y, marker='^', s=200, c='tab:red')
ax.scatter(center2_x, center2_y, marker='v', s=200, c='tab:red')
ax.set_xlim(4, 10)
ax.set_ylim(1, 9)
ax.set_title('CCs after train epoch: %d' % epoch)
x = np.linspace(4, 10, 100)
y = np.linspace(1, 9, 100)
X, Y = np.meshgrid(x, y)
Z = pred_centers(X, Y, centers_all[epoch])
ax.contourf(X, Y, Z, cmap=plt.cm.hot, alpha=0.2)
# 第一列左侧添加y轴标题
if ax.is_first_col():
ax.set_ylabel('Width')
# 最后一行底部添加x轴标题
if ax.is_last_row():
ax.set_xlabel('Length')
plt.subplots_adjust(bottom=0.2,top=0.85,left=0.05,right=0.95)
于是,我们得到了一个分类香蕉和苹果的模型。
香蕉和苹果,因为形态上差异较大,所以只需要两个简单的特征和很少次数的迭代就能将其较好地分开,如果再加入龙蛇果、梨、桃子、黄瓜等形态上分别与他们相近的水果,可能就需要收集更多的特征来训练模型,这种以提取特征为分类依据的方法被称为模式识别,或特征工程。当然也可以用计算机视觉相关的技术获得更优更稳健的模型。这些就不在本文的讨论范围之内了。
希望对你有所启发和帮助!