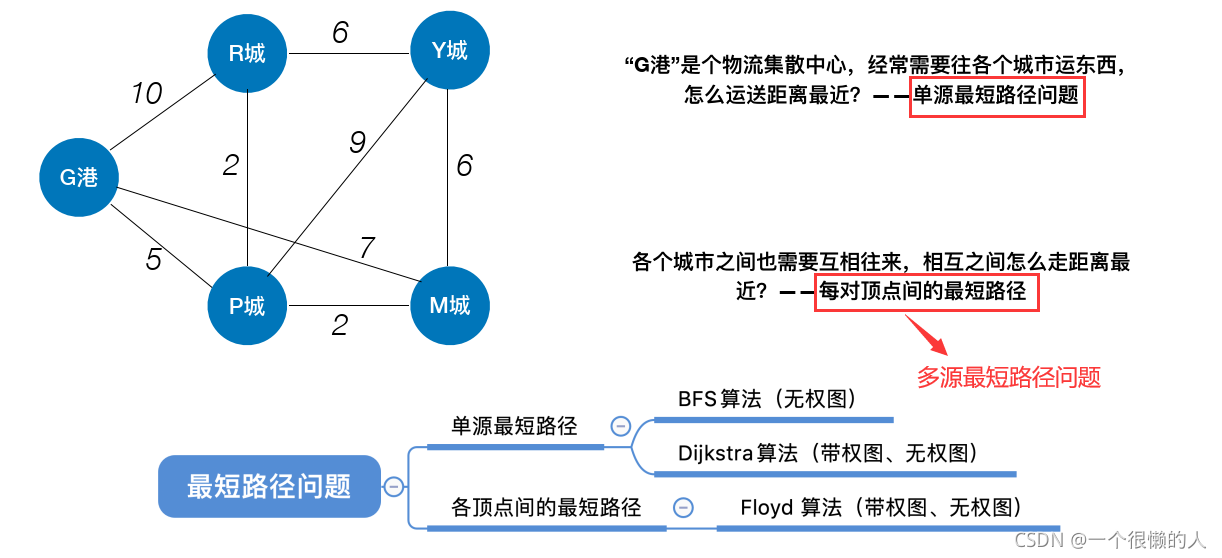
0.概要

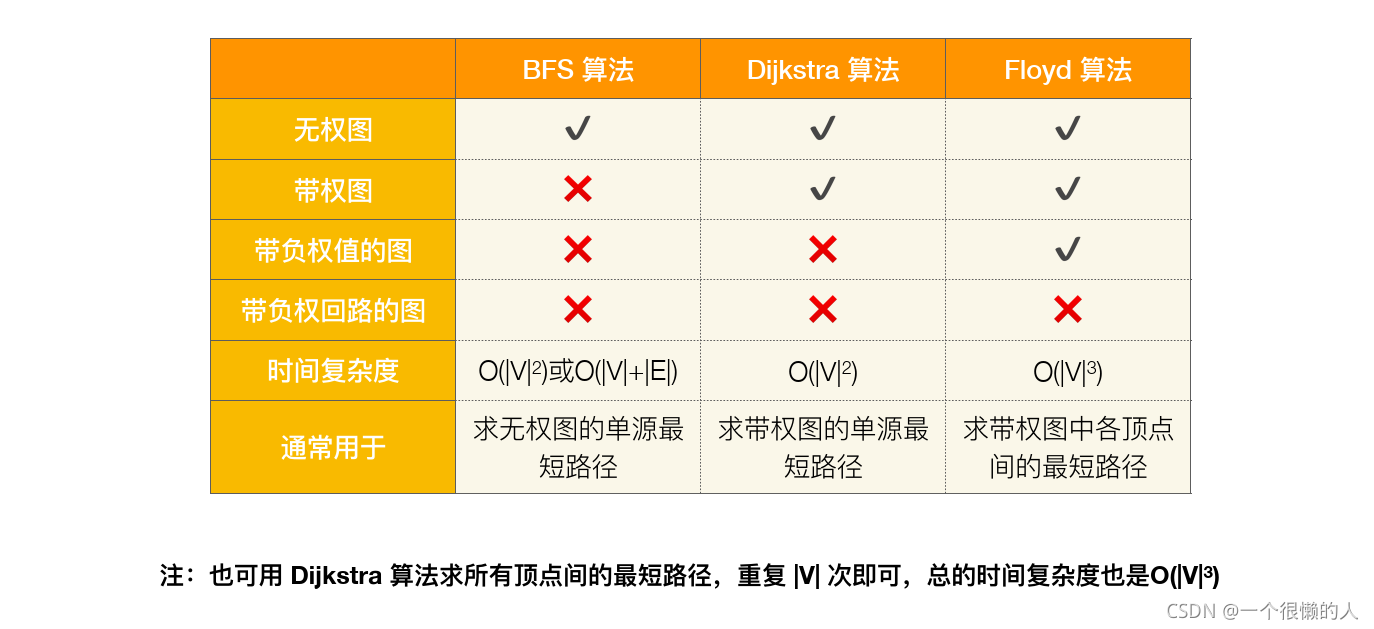
本文主要介绍以下三种方法求解最短路径问题：

1. BFS——单源最短路径问题（简要介绍）
2. Dijkstra_单源最小路径（详细介绍——算法、分析、时间复杂度、实现代码（见文末））
3. 3.Floyd_任意两点最小值（多源最短路径）——（详细介绍——算法、分析、时间复杂度、实现代码（见文末））

问题描述：

解决方法：

---

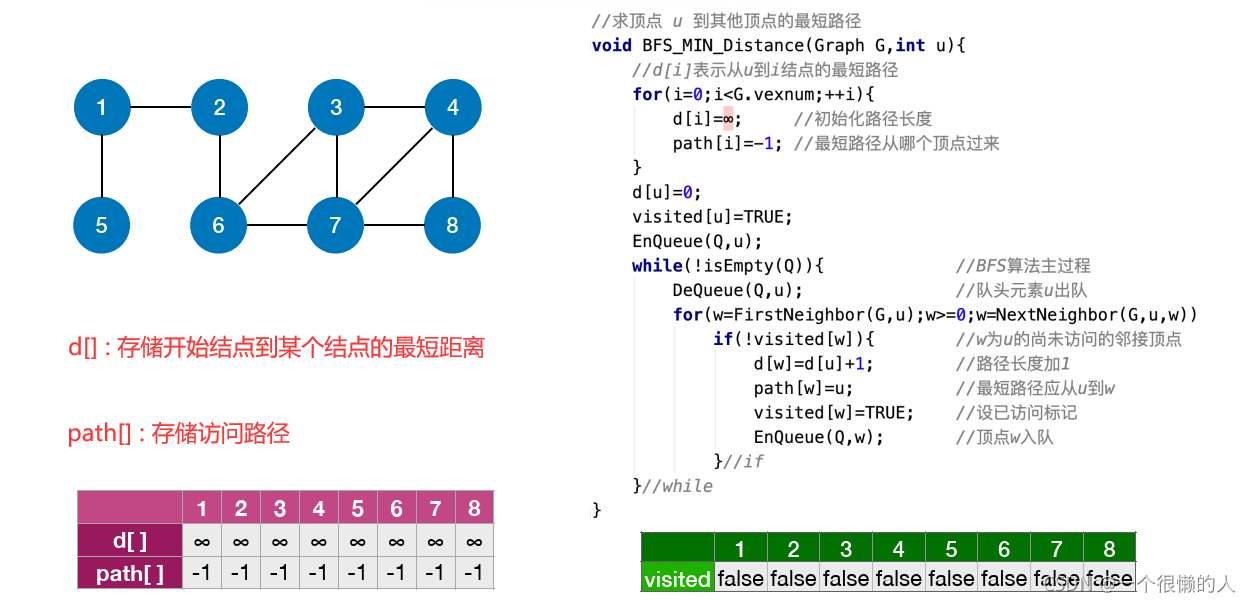
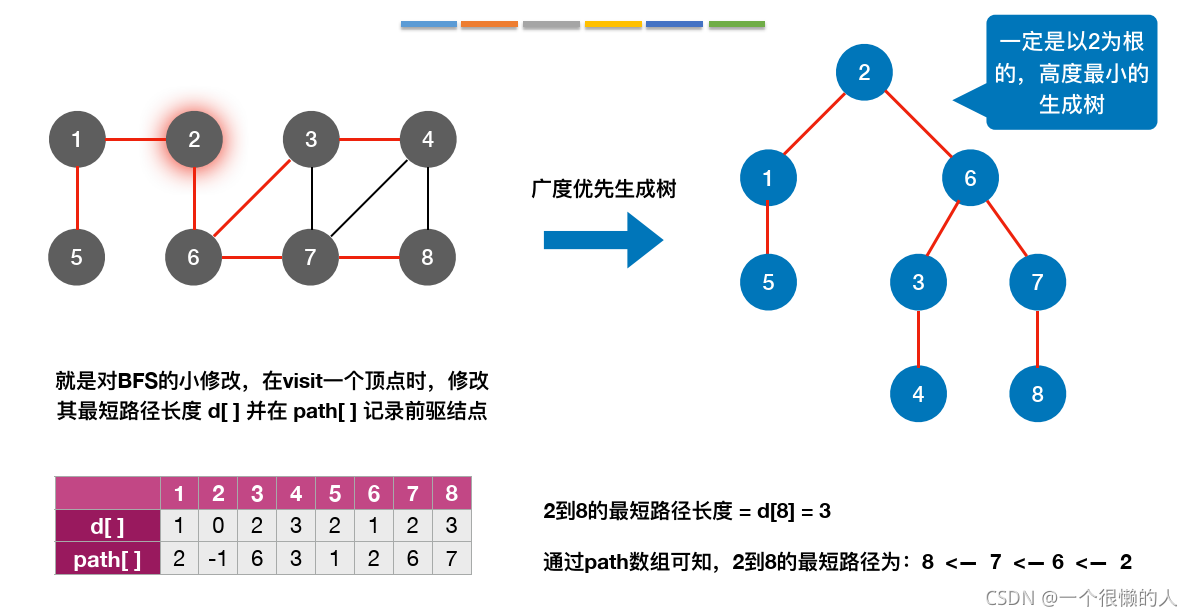
1.BFS——单源最短路径问题（了解即可）

初始化：

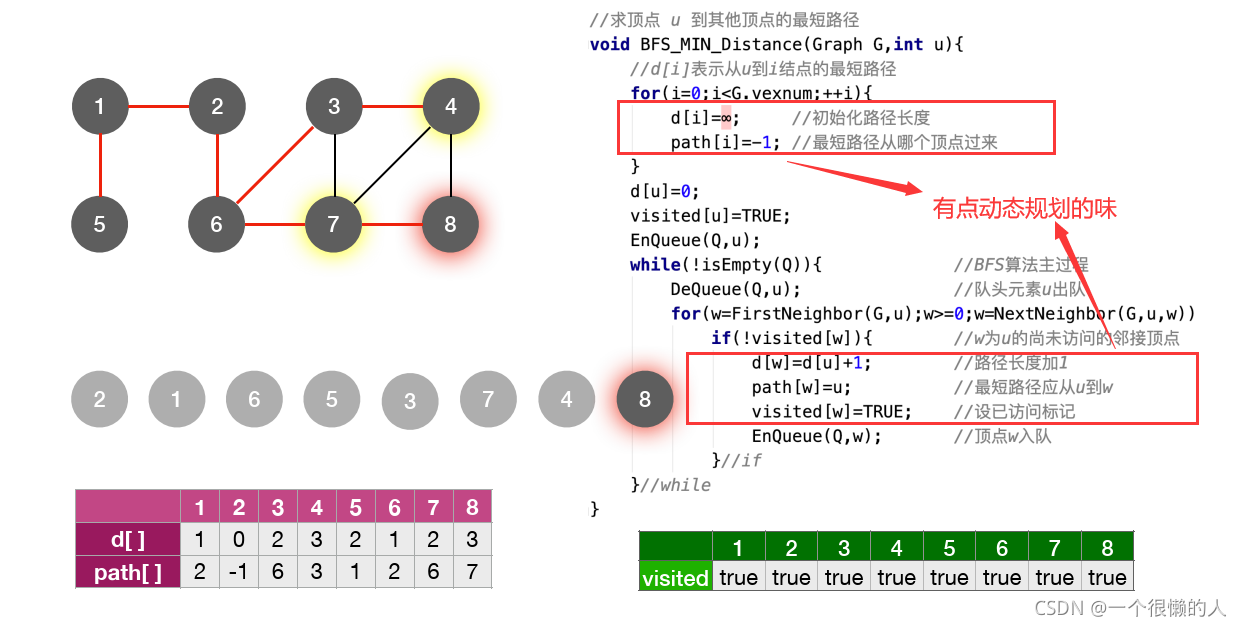
求解完成：

与广度优先生成树的关系：

---

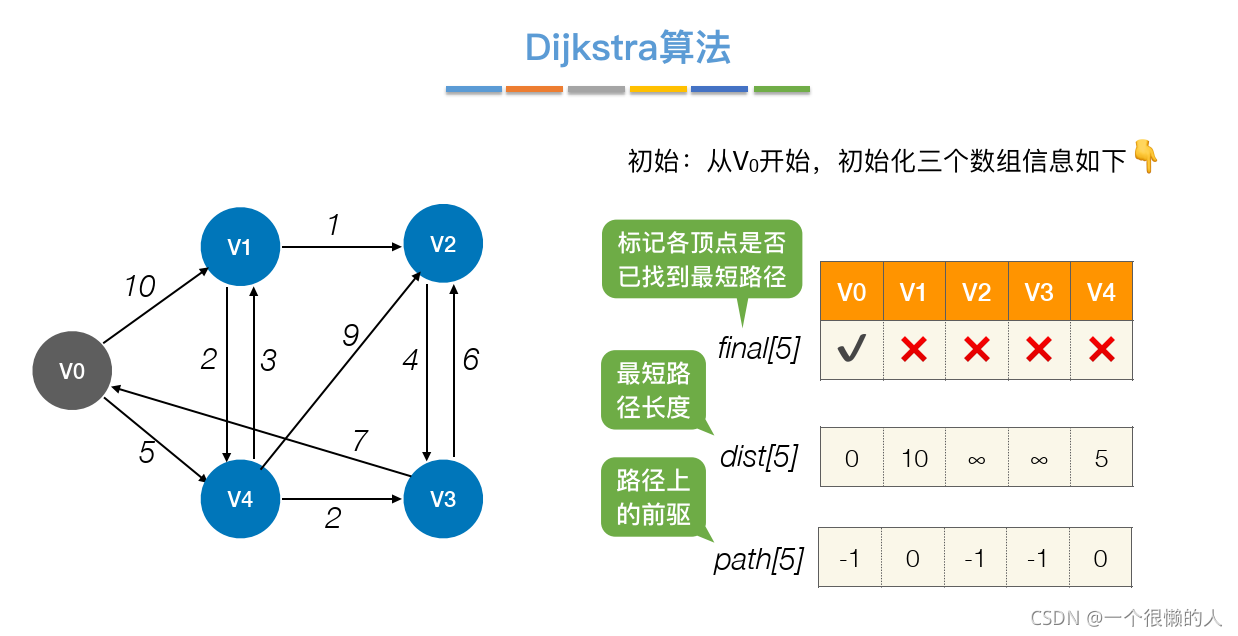
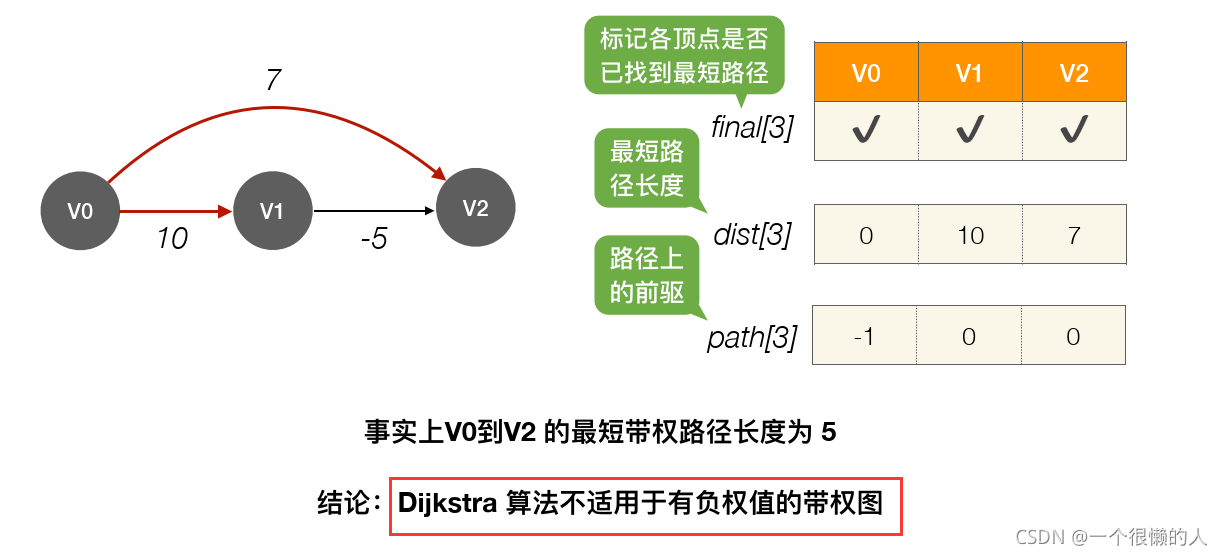
2.Dijkstra_单源最小路径

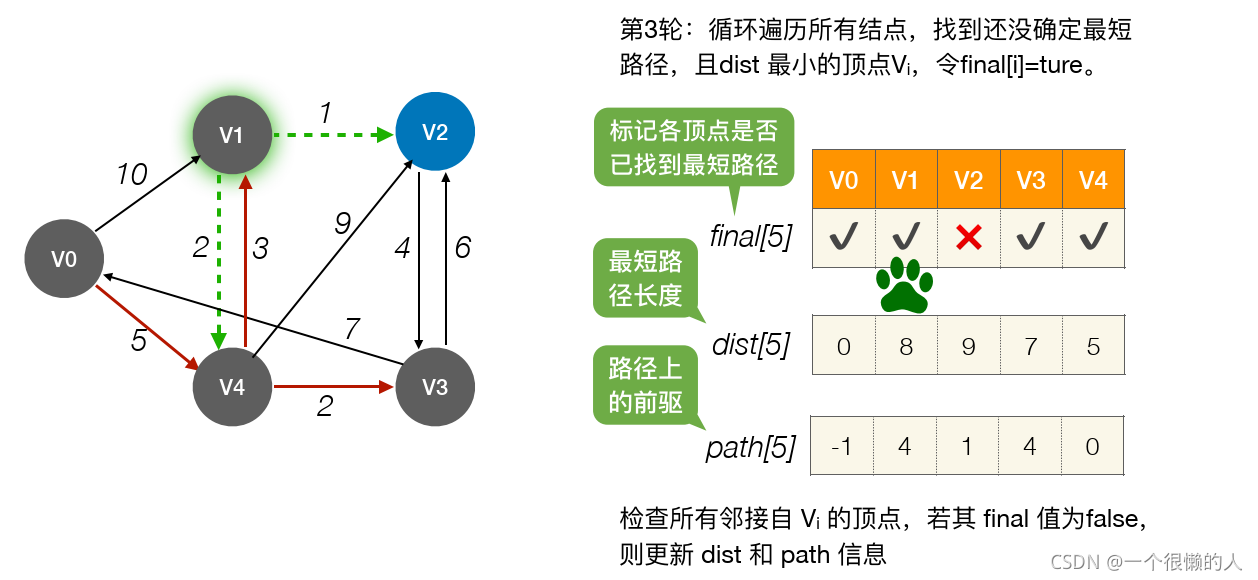
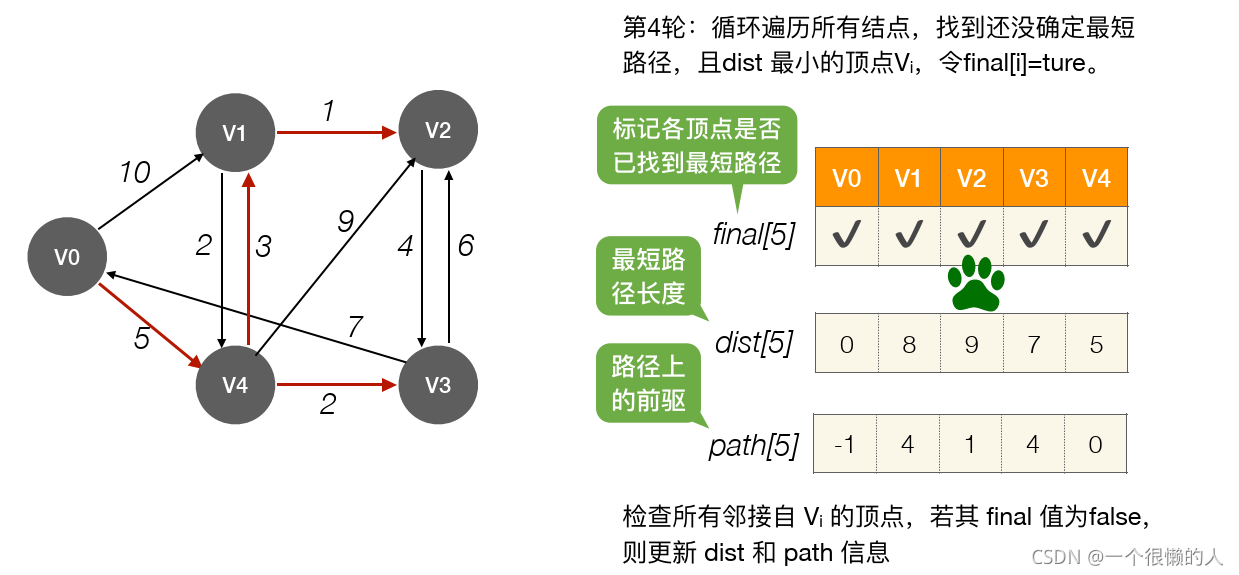
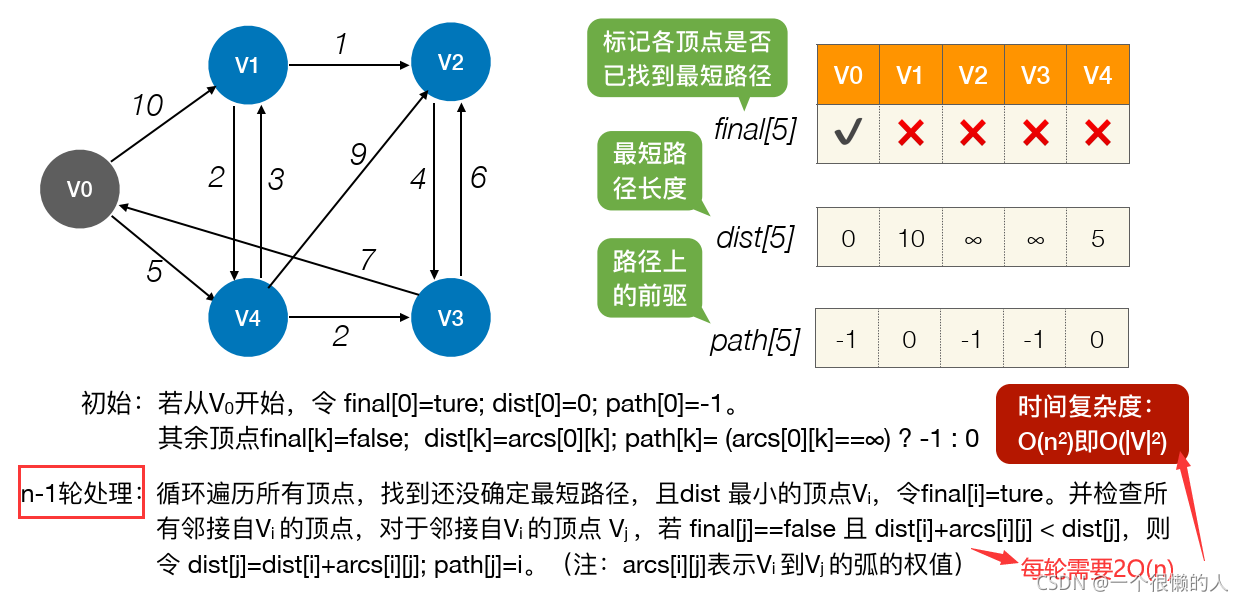
（1）算法思想

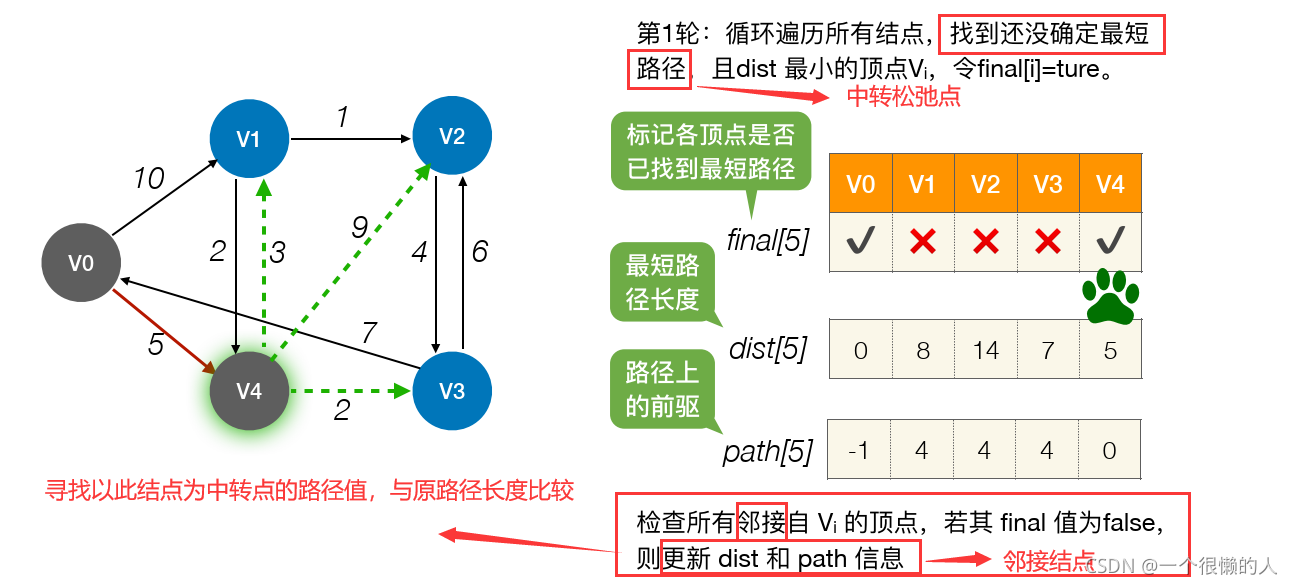
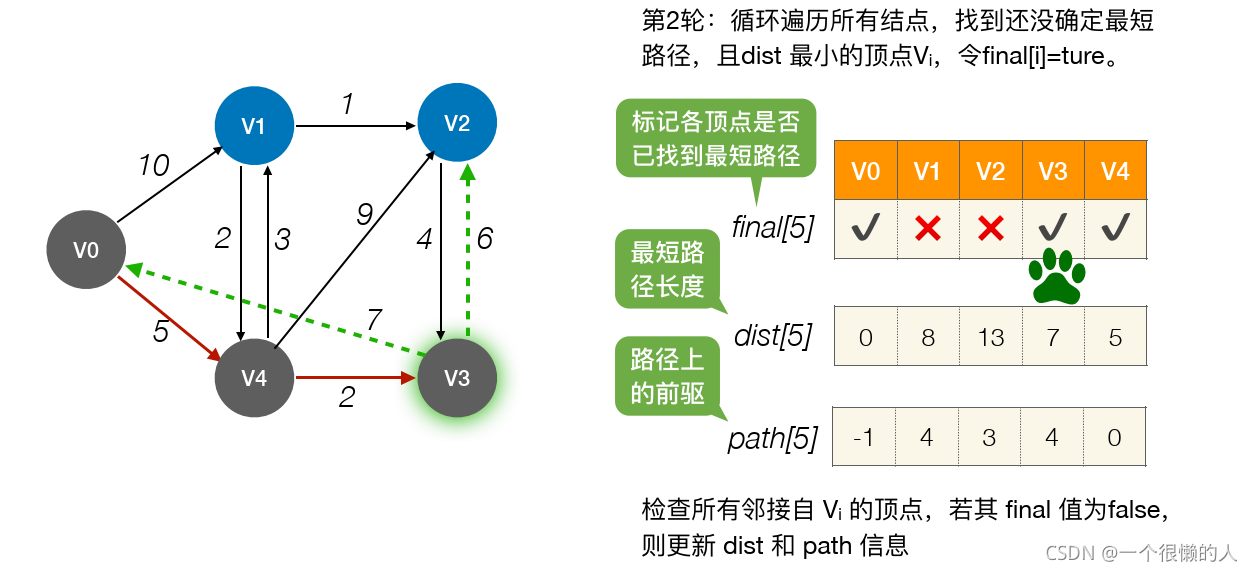
• 此算法算是贪心思想实现的，首先把起点到所有点的距离存下来找个最短的，然后松弛一次再找出最短的，所谓的松弛操作就是，遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近，如果更近了就更新距离，这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。

（2）算法讲解





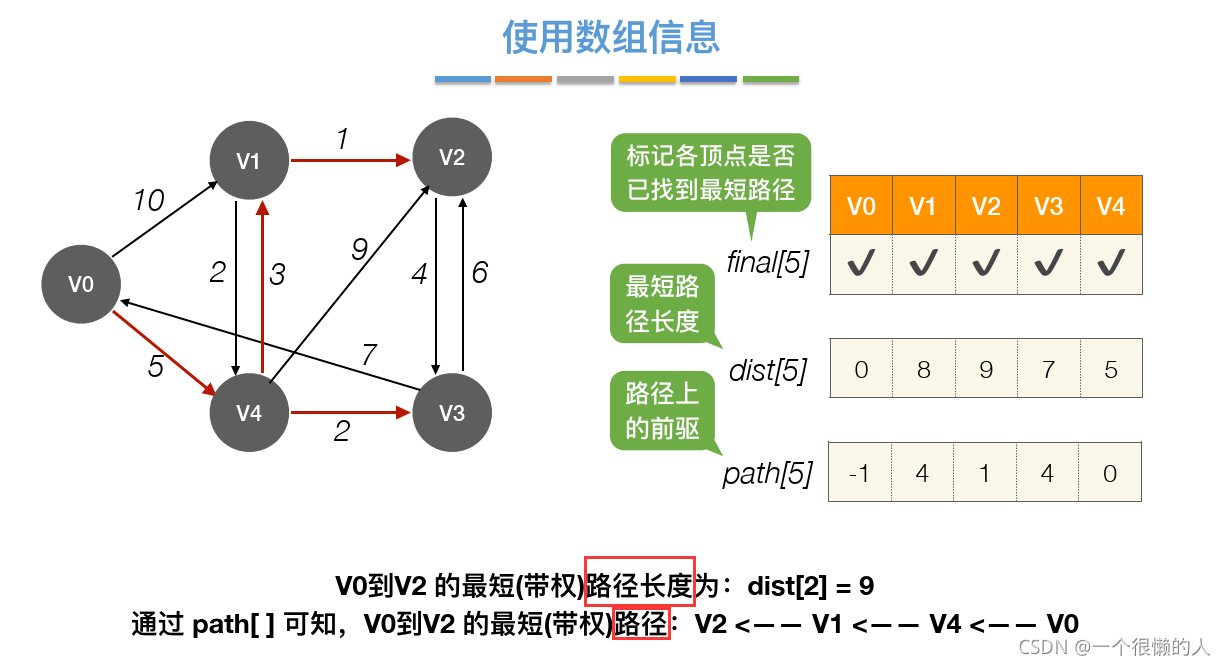
（3）算法结果信息

（4）时间复杂度

（5）注意事项

（6）实现代码

————见文章末尾！！！

---

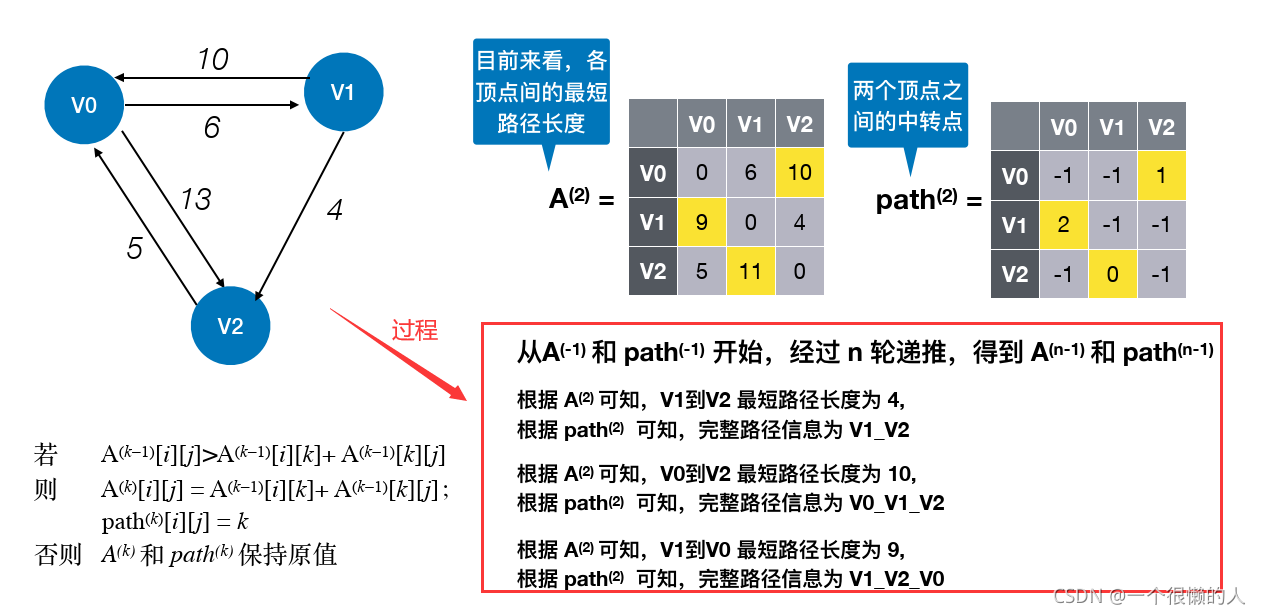
3.Floyd_任意两点最小值（多源最短路径）

（1）算法思想

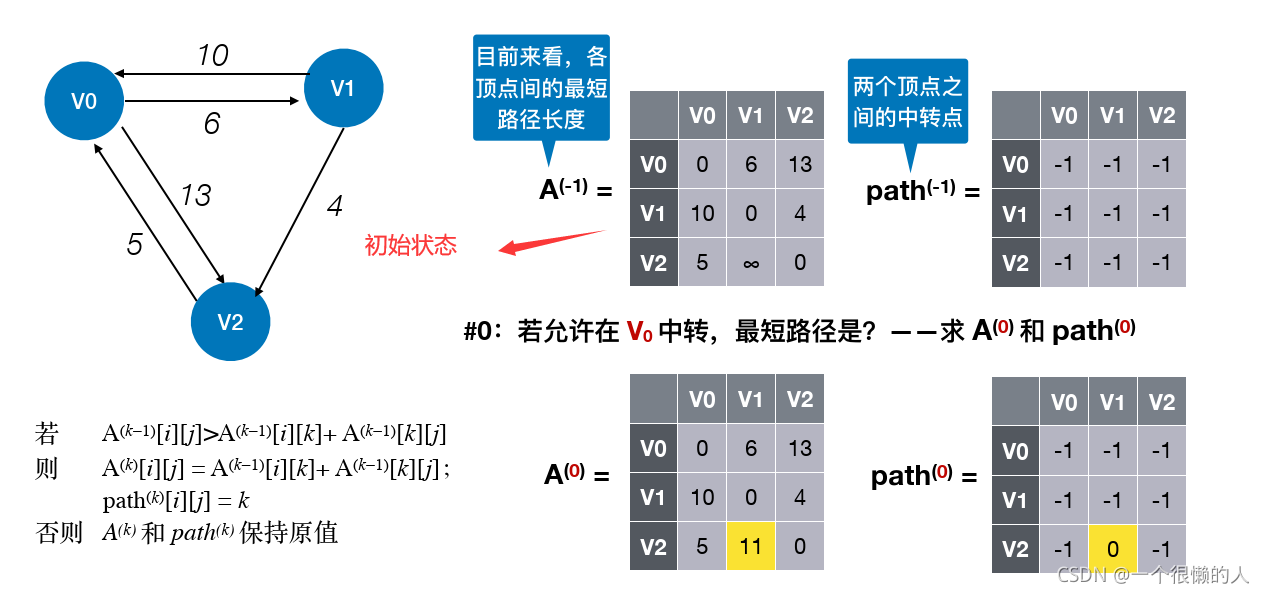
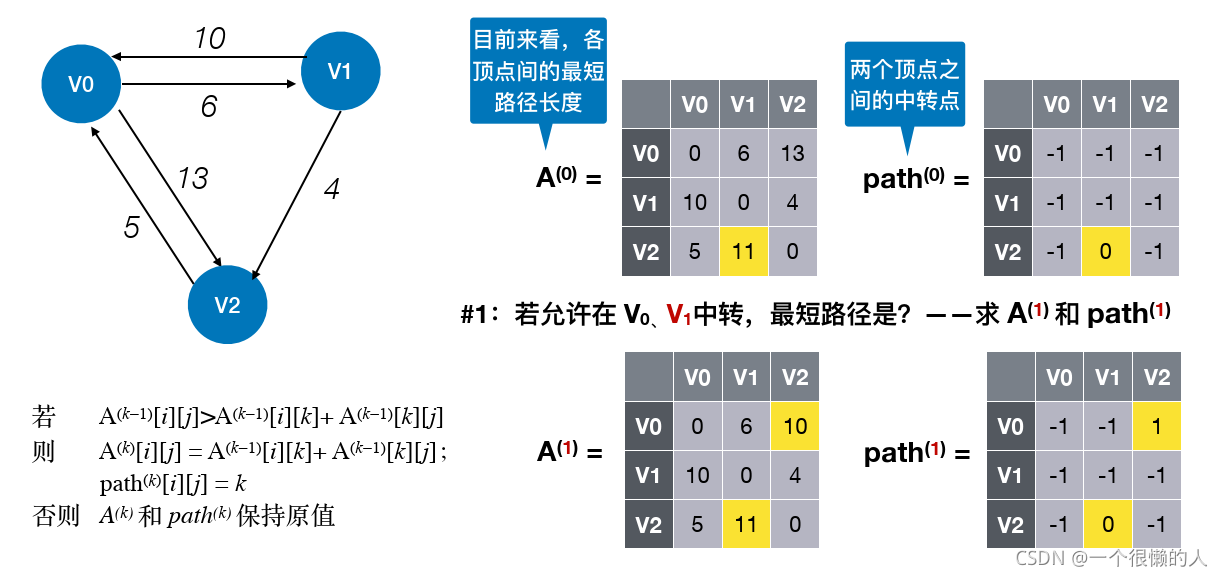
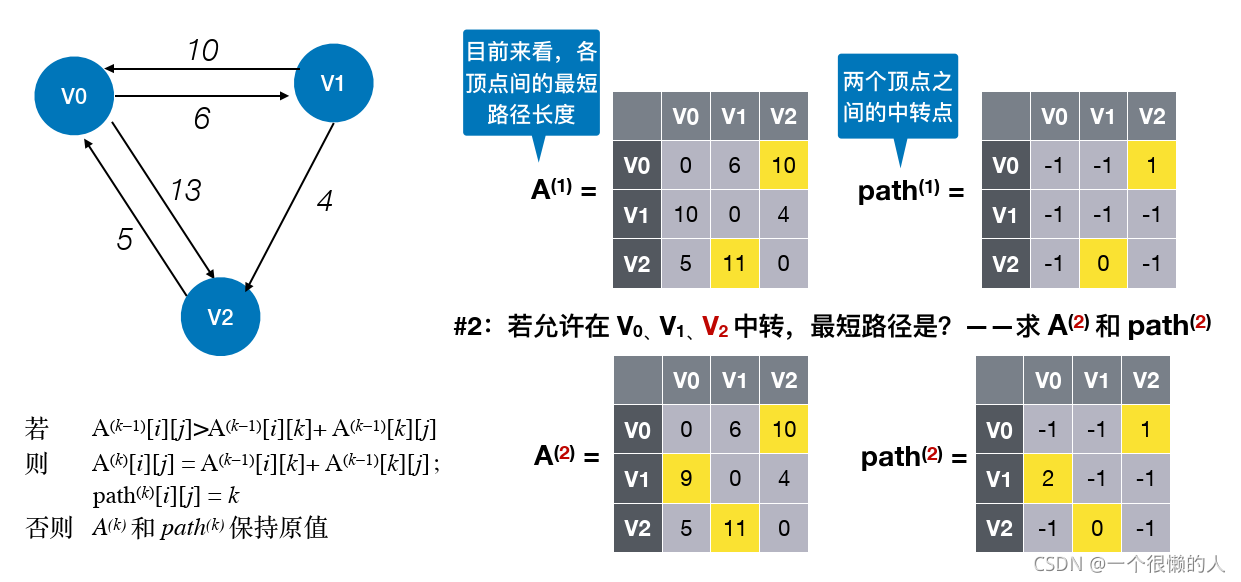
• 此算法动态规划思想实现的，此的遍历方式其实就是先只允许以1号节点进行中转，接着允许以1和2号节点进行中转，再然后允许以1、2、3号节点进行中转……最后允许1-n号节点进行中转，求最短路。每次在枚举k时，得到的是目前经过前k个节点的最短路径。
  

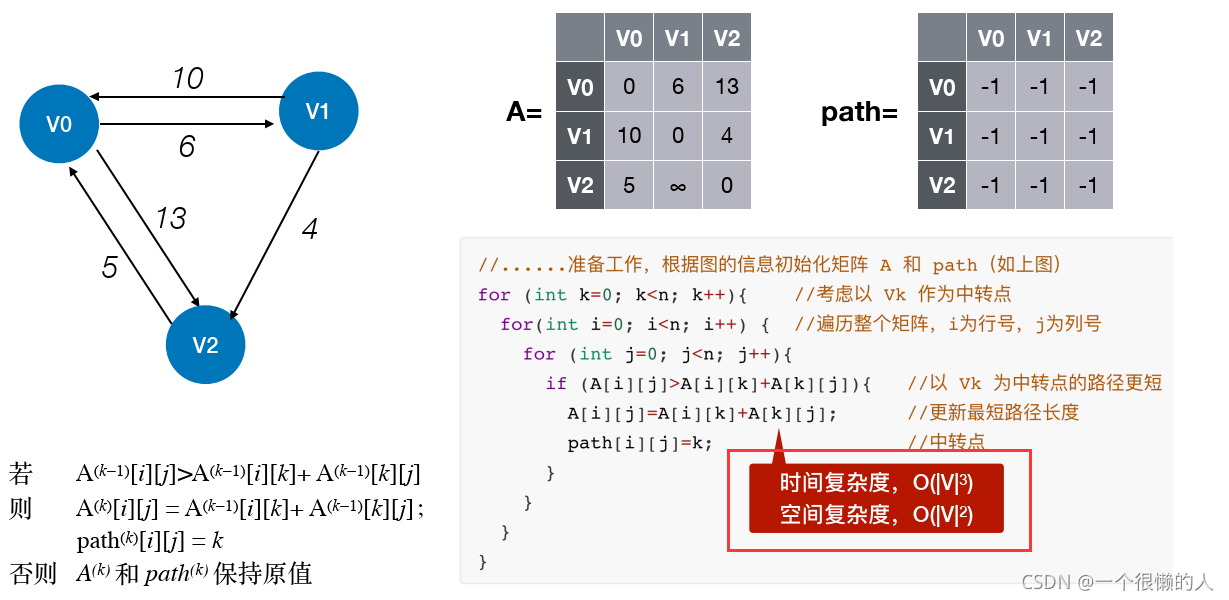
（2）算法讲解




（3）时间复杂度

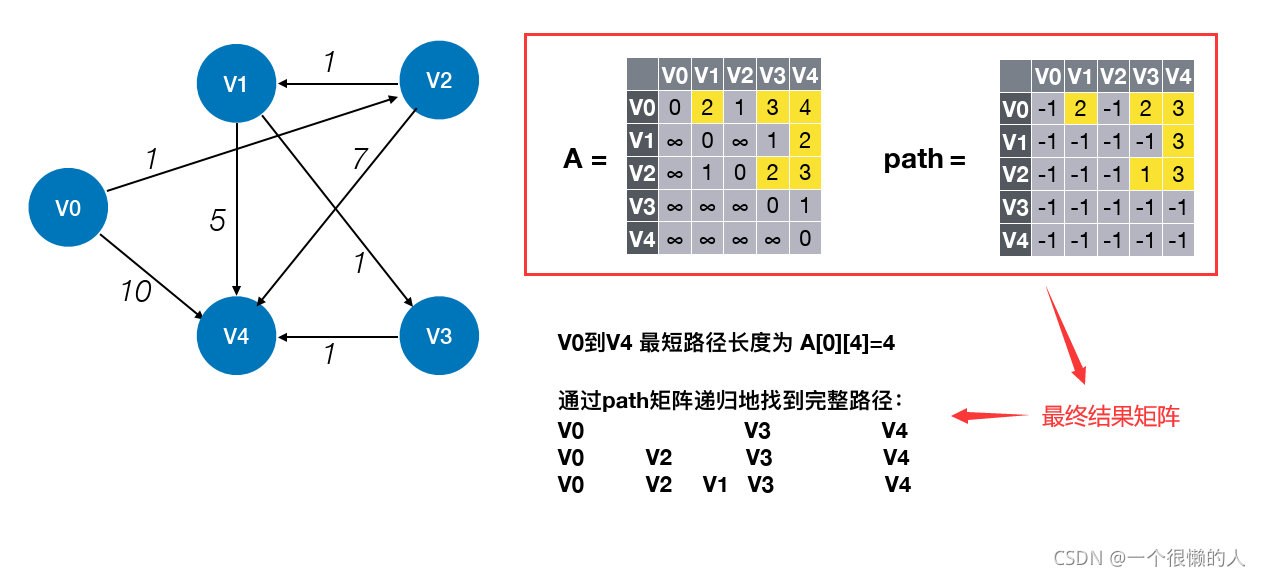
（4）算法结果信息

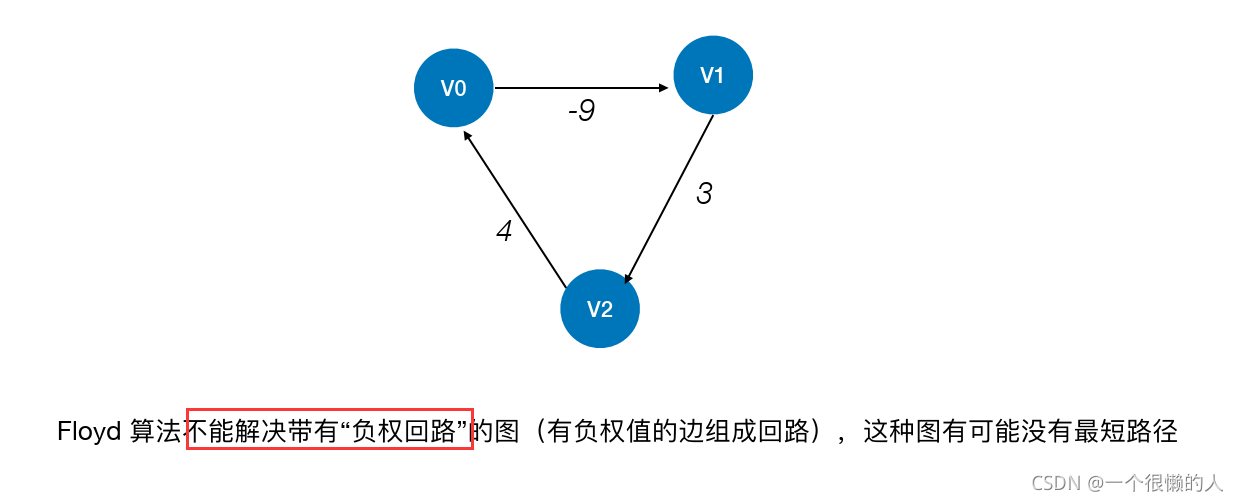
（5）注意事项

• 负权值——可以解决
  
• 负权回路——不能解决
  

（6）实现代码

————见文章末尾！！！

4.实现代码

1.Dijkstra_单源最小路径：

#include<bits/stdc++.h>
using namespace std;

int main(){
	int n,m;
	int inf=999999,u=-1;
	cin>>n>>m;
	int e[n+1][n+1]; 
	int dis[n+1];	//标记1到i点的最小距离 
	int flag[n+1];	//标记已被访问的松弛点 
	
	memset(flag,0,sizeof(flag));	//初始化为0 
	
	//初始化
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i==j){
				e[i][j]=0;
			}else{
				e[i][j]=inf;
			}
		}
	}
	
	//初始化边 
	for(int i=1;i<=m;i++){
		int x,y,z;
		cin>>x>>y>>z;
		e[x][y]=z;
	}
	
	//初始化dis
	for(int i=1;i<=n;i++){
		dis[i]=e[1][i];
	}
	flag[1]=1; 
	
	//关键代码
	for(int k=1;k<n;k++){
		int min=inf;
		//寻找松弛点——还没确定 从起点到以某个点结尾的最短路径的点 
		for(int i=1;i<=n;i++){
			if(flag[i]==0&&dis[i]<min){
				u=i;
				min=dis[i];
			}
		} 
		//标记
		flag[u]=1;
		
		//进行松弛
		for(int v=1;v<=n;v++){
			if(e[u][v]<inf){
				if(dis[v]>dis[u]+e[u][v]){
					dis[v]=dis[u]+e[u][v];
				}
			}
		} 
	}
	
	//输出结果——起点到各个结点的最短距离 
	for(int i=1;i<=n;i++){
		cout<<setw(3)<<dis[i];
	}	
	
	return 0;
}

2.Floyd_任意两点最小值:

#include<bits/stdc++.h>
using namespace std;
/*
eg(input)： 
4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12
eg:(output)
  0  2  5  4
  9  0  3  4
  6  8  0  1
  5  7 10  0
*/

int main(){
	int n;	//多少个顶点
	int m;	//多少条边
	
	int inf=99999999;
	
	cin>>n;
	cin>>m;
	
	int e[n+1][n+1];

	//初始化
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i==j){
				e[i][j]=0;
			}
			else{
				e[i][j]=inf;
			}
		}
	} 
	
	//输入边的信息
	for(int i=1;i<=m;i++){
		int x,y,z;
		cin>>x>>y>>z;
		e[x][y]=z;	//存储边的信息 
	} 
	
	//Floyd算法:三层循环、一层中转点，二层边的起点、三层终止节点 
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				//找出通过中转点的最小值 
				e[i][j]=min(e[i][j],e[i][k]+e[k][j]);
			}
		}
	} 
	
	//输出结果
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			//输出每两个节点的最小距离
			cout<<setw(3)<<e[i][j]; 
		}
		cout<<endl;
	}
	 
	return 0;
}