粒子滤波实现刀具寿命预测(附python代码)
(代码更新,增加重采样函数)
背景介绍
刀具失效是加工过程中的主要问题,通过多特征融合方法实现刀具磨损量预测后建立了刀具的健康指标。接下来就是利用得到的健康指标对刀具的剩余寿命进行预测。粒子滤波则是一种常用的方法。
关于粒子滤波的理论知识参见粒子滤波理论。
本文主要讲解通过python简单实现基于粒子滤波的刀具寿命预测思路以及简要的代码。
粒子滤波的主要流程
1、建立刀具退化模型。结合刀具退化规律,一般情况下我们使用双指数模型。即:
那么[a、b、c、d]就是我们需要通过估计的模型参数。
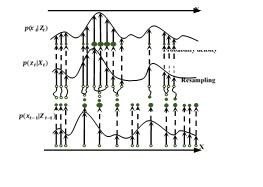
2、 初始化参数与粒子集初始化。 k = 0 \ k=0 k=0时根据先验生成M个 x 0 \ x_0 x0采样粒子,即:{ x 0 ( i ) x_0^{(i)} x0(i)} i = 1 M \ _{i=1}^M i=1M。
3、 进行粒子滤波。对于 k = 1 , 2 , 3... t \ k=1,2,3...t k=1,2,3...t
(1)重要性采样。生成采样粒子{ x k ( i ) x_k^{(i)} xk(i)} i = 1 M \ _{i=1}^M i=1M,计算粒子权值 w k w_k wk,并归一化;
(2)重采样。重采样后的粒子集为{ x k ( i ) , 1 / M x_k^{(i)},1/M xk(i),1/M};
(3)输出。计算 k k k时刻的状态估计值, x ^ = \widehat{x}= x = ∑ i = 1 M x k ( i ) w k ( i ) \sum_{i=1}^{M} x_k^{(i)}w_k^{(i)} ∑i=1Mxk(i)wk(i)。
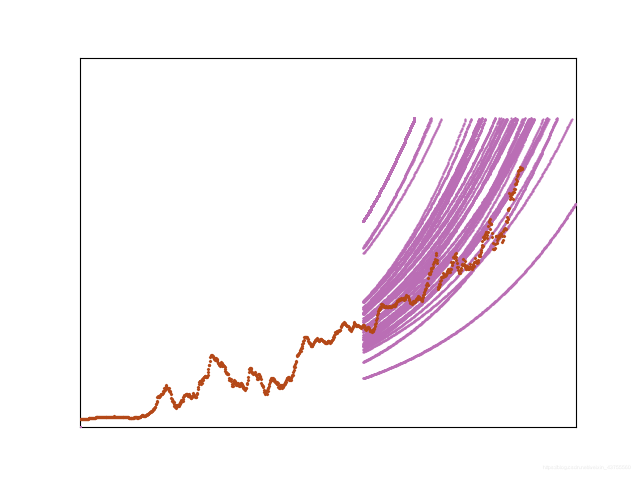
4、 剩余寿命预测。将粒子集参数带入刀具退化模型完成寿命预测。
(1)将M个粒子带入退化模型得到刀具当前状态后的退化趋势;
(2)设定阈值,当磨损状态超过阈值后即判断刀具失效,通过剩余寿命方程 L t = i n f \ L_t=inf Lt=inf{ l t : Y ( t + l t ) ≥ D , t > 0 \ l_t:Y(t+l_t)≥D,t>0 lt:Y(t+lt)≥D,t>0}得到M个粒子的刀具剩余寿命。
(3)取M个粒子得到的剩余寿命的均值作为最终的刀具剩余寿命。
居中并且带尺寸的图片:
相关代码
初始化
##initial value of model parameters
a = 0.01475
b = 0.0556
c = 0.255
d = 0.0037
X0 = np.array([[a], [b], [c], [d]])
##Parameters for Particle Filter
M = 100 #粒子个数
p = 4 #参数个数
Xparam = np.zeros([p, N])
Xparam[:,0] = X0[:,0]
##Process Noise and Measurement Noise
var_a = 0.000001
var_b = 0.01
var_c = 0.1
var_d = 0.0001
sd_z = 1E-4
Q = sd_z * np.diag([var_a, var_b, var_c, var_d])
F = np.eye(p)
R = 0.001
##Monte Carlo Simulation 粒子集初始化
Xm = np.zeros([p, M, N])
for i in range(0, M):
dx1 = X0 + np.dot(sl.sqrtm(Q), np.random.randn(p, 1))
Xm[:, i, 0] = dx1[:,0]
粒子滤波
# Particle Filter Initialization
Zm = np.zeros([M, start])
A_estimated = np.zeros([1, start])
B_estimated = np.zeros([1, start])
C_estimated = np.zeros([1, start])
D_estimated = np.zeros([1, start])
W = np.zeros([start, M])
Zpf = np.zeros([M, start])
#Particle Filtering
for k in range(2, N+1):
#state transition equations
for i in range(0, M):
Xm[0,i,k-1] = Xm[0,i,k-2] + np.sqrt(var_a*sd_z)*np.random.randn()
Xm[1,i,k-1] = Xm[1,i,k-2] + np.sqrt(var_b*sd_z)*np.random.randn()
Xm[2,i,k-1] = Xm[2,i,k-2] + np.sqrt(var_c*sd_z)*np.random.randn()
Xm[3,i,k-1] = Xm[3,i,k-2] + np.sqrt(var_d*sd_z)*np.random.randn()
#Weighing of particles
for i in range(0, M):
Zm[i, k - 1] = Xm[0, i, k - 1] * np.exp(Xm[1, i, k - 1] * k) \
+ Xm[2, i, k - 1] * np.exp(Xm[3, i, k - 1] * k) + sd_z * np.random.randn()
W[k - 1, i] = (1 / np.sqrt(2 * np.pi * R)) \
* np.exp(-(Z_measured1[k - 1] - Zm[i, k - 1]) ** 2 / (2 * R))
#Resampling based on weights
W[k - 1, :] = W[k - 1, :] / np.sum(W[k - 1, :]) # 权值归一化
dx3 = []
for i in range(1, M + 1):
dx3.append(i)
dx3 = np.array(dx3)
outIndex = sim_resample(dx3, np.array([W[k - 1, :]]).T) # 随机重采样
Xm[:, :, k - 1] = Xm[:, outIndex[:], k - 1] # 得到新的样本集
W[k - 1, :] = 1/M #得到新的样本集
#value of particles
# Mean value of particles
A_estimated[0, k - 1], _ = estimate(Xm[0, :, k - 1], W[k-1, :])
B_estimated[0, k - 1], _ = estimate(Xm[1, :, k - 1], W[k-1, :])
C_estimated[0, k - 1], _ = estimate(Xm[2, :, k - 1], W[k-1, :])
D_estimated[0, k - 1], _ = estimate(Xm[1, :, k - 1], W[k-1, :])
X_param[:, k - 1] = [np.median(A_estimated[:, k - 1]), np.median(B_estimated[:, k - 1]),
np.median(C_estimated[:, k - 1]), np.median(D_estimated[:, k - 1])] # 滤波后的参数
Zpf = np.zeros([1, noOfCycles])
Xpf = np.zeros([1, noOfCycles])
for k in range(int(start), noOfCycles):
Zpf[0, k - start] = X_param[0, -1] * np.exp(X_param[1, -1] * k) \
+ X_param[2, -1] * np.exp(X_param[3, -1] * k) + sd_z * np.random.randn()
Xpf[0, k - start] = k
# 剩余寿命预测
if Zpf[0, k - start] >= threshold_capacity:
failure_index = k
break
noOfCyclesLeft = failure_index - start
重采样函数与状态估计函数
# 重采样函数
def sim_resample(m, weights):
N = len(m)
cumulative_sum = np.cumsum(weights)
cumulative_sum[-1] = 1.
rn = np.random.rand(N)
indexes = np.searchsorted(cumulative_sum, rn)
return indexes
# estimation
def estimate(particles, weights):
mean = np.average(particles, weights=weights)
var = np.average((particles - mean) ** 2, weights=weights)
return mean, var