动态规划

90% 的字符串问题都可以用动态规划解决，并且90%是采用二维数组。

一、动态规划的三大步骤

动态规划，无非就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。

动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

最优子结构指的是，问题的最优解包含子问题的最优解。反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。

动态规划题三个重要步骤：

1、定义数组元素的含义。

上面说了，我们会用一个数组，来保存历史数组，假设用一维数组 dp[] 吧。这个时候有一个非常非常重要的点，就是规定你这个数组元素dp[i]的含义。一般来说dp[i]直接与所求答案关联。

2、找出数组元素直接的关系式（状态转移方程）

动态规划的题，就是把一个规模比较大的问题分成几个规模比较小的问题，然后由小的问题推导出大的问题。

大部分情况下，dp[i] [j] 和 dp[i-1] [j]、dp[i] [j-1]、dp[i-1] [j-1] 肯定存在某种关系。我们可以从最后一步、倒数第二步等方面入手分析。

3、找出初始值

动态规划类似于数学归纳法，我们需要知道初始值，才能不断地推下去。一般来说，如果是一维数组，初始值一般为为dp[0] ，dp[1]，dp[2]等；如果是二维数组，一般为dp[0] [0] ，dp[i] [0] (i>=1) ，dp[0] [j] (j>=1)等

在做题的时候，按照以上三个步骤进行刻意练习，达到融会贯通！

二、案例分析

案例一：跳台阶

剑指 Offer 10- II. 青蛙跳台阶问题

题目

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：2

示例 3：

输入：n = 0
输出：1

解题思路：

题目分析：青蛙每次有两种选择，跳一级或两级，当青蛙跳上第n级的前一步，青蛙有两种状态，即在第n-1级或第n-2级，那么当青蛙跳上第n级的跳法 = 第n-1级跳法 + 第 n-2 级跳法。符合最优子结构性质，使用动规。

使用刻意练习进行三大步骤思考：

1、数组元素的含义：dp[i]表示，当青蛙跳上第i级台阶时的跳法数量。我们所求答案为dp[n];

2、状态转移方程：dp[i] = dp[i-1] + dp[i-2] (i>=2)

3、初始值：dp[0] =1 dp[1]=1

代码如下：

var numWays = function (n) {
  //特判
  if (n <= 1) {
    return 1;
  }

  let dp = new Array(n + 1);
  dp[0] = 1;
  dp[1] = 1;
  for (let i = 2; i <= n; i++) {
    dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
  }
  return dp[n];
}

案例二：路径数

leetcode 62 不同路径

题目

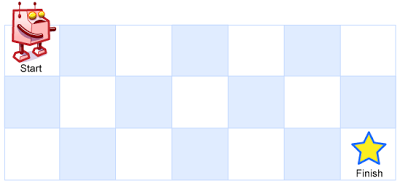
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

解题思路：

对题目进行分析：题目要求机器人到达右下角的路径数，当机器人到达右下角的前一步，只能在右下角上方和右下角左方，这个时候到达右下角的路径数 = 右下角上方路径数 + 右下角左方路径数。

使用刻意练习的思路思考：

1、定义数组元素含义。dp[i] [j] 表示机器人到达（i , j) 坐标时的路径数。我们所求为dp[m-1] [n-1]。

2、状态转移方程：dp[i] [j] = dp[i-1] [j] + dp[i] [j-1]；

3、初始值：

• 第一行，机器人只能向右走，此时dp[0] [i] = 1 ( i>=0)
• 第一列，机器人只能向下走，此时dp [i] [0] = 1 (i>=0)

代码如下：

var uniquePaths = function (m, n) {
  let dp = new Array(m);
  for (let i = 0; i < m; i++) {
    dp[i] = new Array(n);
  }

  //初始化
  for (let i = 0; i < m; i++) {
    dp[i][0] = 1;
  }

  for (let i = 0; i < n; i++) {
    dp[0][i] = 1;
  }

  //状态转移
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    }
  }
  return dp[m - 1][n - 1];
}

案例三：最小路径和

leetcode 64 最小路径和

题目

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步。

示例 1：

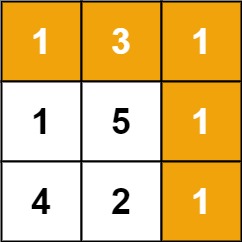
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

解题思路：

对题目进行分析：求从左上角到右下角的路径和最小，到达右下角的前一步为右下角上方或右下角左方，则右下角的路径和最小 = Min(右下角上方路径和，右下角左方路径和) + 右下角的值。

使用刻意练习的思路思考：

1、定义数组元素的含义。dp[i] [j] 为机器人到达（i , j )位置的路径最小和。我们所求为dp [m-1] [n-1]。

2、状态转移方程：dp[i] [j] = Math.min(dp[i-1] [j] , dp[i] [j-1]) +grid[i] [j]。（i>=1,j>=1)

3、初始值：

• dp[0] [0] = grid[0] [0]
• 第一行，机器人只能往右走，路径最小和为前一个格子路径最小和 + 当前格子的值。dp[0] [i] = dp[0] [i-1] + grid[0] [i ] (i>=1)
• 第一列，机器人只能往下走。dp[i] [0] = dp[i-1] [0] + grid[i] [0] (i>=1)

代码如下：

var minPathSum = function (grid) {
  let m = grid.length
  let n = grid[0].length;

  let dp = new Array(m);
  for (let i = 0; i < m; i++) {
    dp[i] = new Array(n);
  }

  //初始化
  dp[0][0] = grid[0][0];
  for (let i = 1; i < n; i++) {
    dp[0][i] = dp[0][i - 1] + grid[0][i];
  }

  for (let i = 1; i < m; i++) {
    dp[i][0] = dp[i - 1][0] + grid[i][0];
  }

  //状态转移方程
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
    }
  }
  return dp[m - 1][n - 1];
}

案例四：编辑距离

题目

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

解题思路：

对题目进行分析：要将word1 转换成 word2 ，每次我们有三种选择 插入、删除、替换，求最少操作次数，整个单词转换的最少操作次数依赖于前面单词转换的最少次数，符合最优子结构，可以使用动态规则。

按照刻意练习的思路进行思考：

1、定义数组元素的含义。dp[i] [j]表示，长度为i的word1 转换成长度为j的word2所需要的的最少操作数。我们所求的答案为dp[len1] [len2] (len1 = word1.length ; len2 = word2.length)。

2、状态转移方程。我们需要对word进行分析，如果word1[i-1] 和 word2[j-1]相等，不用做任何操作；如果不等，我们需要从增删改中进行选择操作数最少的。

注意！！！长度为i ，最后一个字符为word1[i-1]！！！

• 如果word1[i-1] === word2[j-1] ，则dp[i] [j] = dp[i-1] [j-1]；

• 如果word1[i-1] !== word2[j-1]

  • 选择在i后插入一个word2[j-1]，dp[i] [j] = dp[i] [j-1] +1 ;

    理解：在i后插入一个word2[j]，则需要保证前i个字符与j-1个字符相同。
    

  • 选择删除word1[i] ，dp[i] [j] = dp[i-1] [j]+1;

  • 选择替换字符，word1[i-1]变为word2[j-1]，dp[i] [j] =dp[i-1] [j-1] +1;

  选择操作数最少，即dp[i] [j] = Math.min(dp[i] [j-1] ,dp[i-1] [j] ,dp[i-1] [j-1]) +1;

3、初始值：

• dp[0] [0] = 0;
• 其中一个单词为空串时，就是一直进入删除或插入操作
  • dp[0] [i] = dp[0] [i-1] +1 ;(i >=1) 不断插入字符
  • dp[i] [0] = dp[i-1] [0] +1 ;(i >=1) 不断删除字符

代码如下：

var minDistance = function (word1, word2) {
  let len1 = word1.length;
  let len2 = word2.length;

  let dp = new Array(len1 + 1);
  for (let i = 0; i <= len1; i++) {
    dp[i] = new Array(len2 + 1);
  }

  //初始化
  dp[0][0] = 0;
  for (let i = 1; i <= len1; i++) {
    dp[i][0] = dp[i - 1][0] + 1;
  }
  for (let i = 1; i <= len2; i++) {
    dp[0][i] = dp[0][i - 1] + 1;
  }

  //状态转移
  for (let i = 1; i <= len1; i++) {
    for (let j = 1; j <= len2; j++) {
      if (word1[i - 1] === word2[j - 1]) {
        dp[i][j] = dp[i - 1][j - 1];
      } else {
        dp[i][j] = Math.min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]) + 1;
      }
    }
  }
  return dp[len1][len2];
};

console.log(minDistance("horse", "ros"));