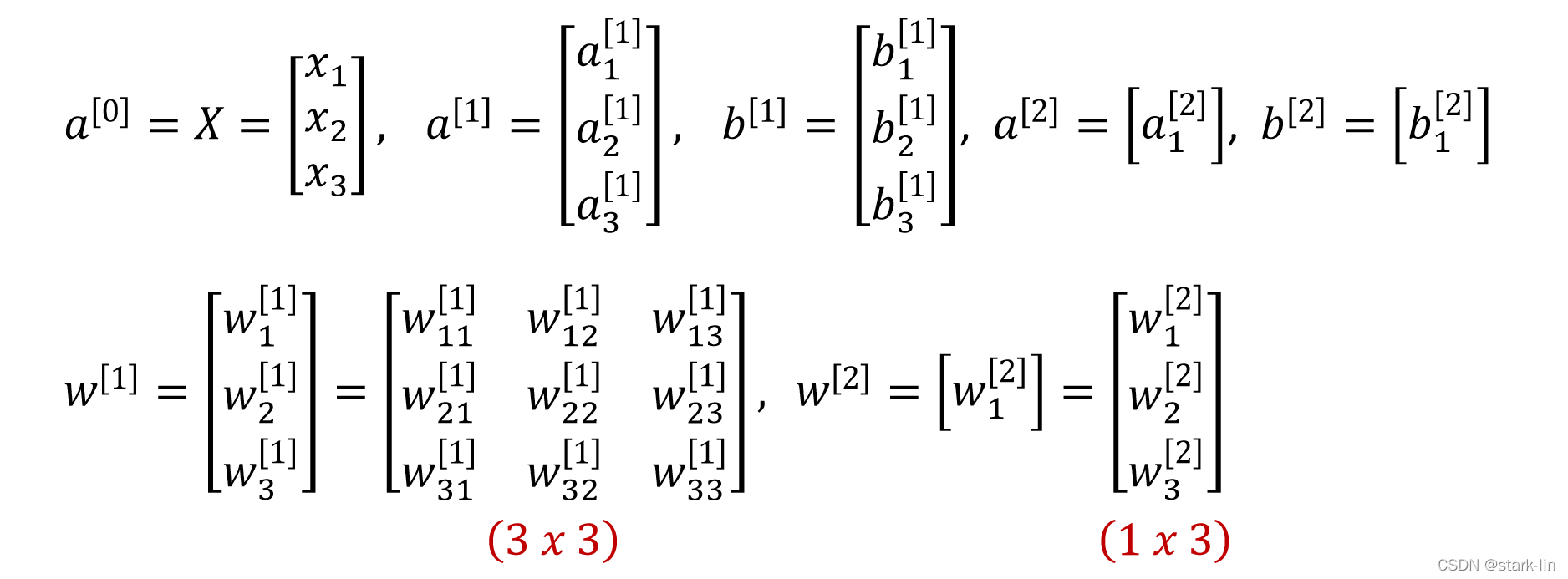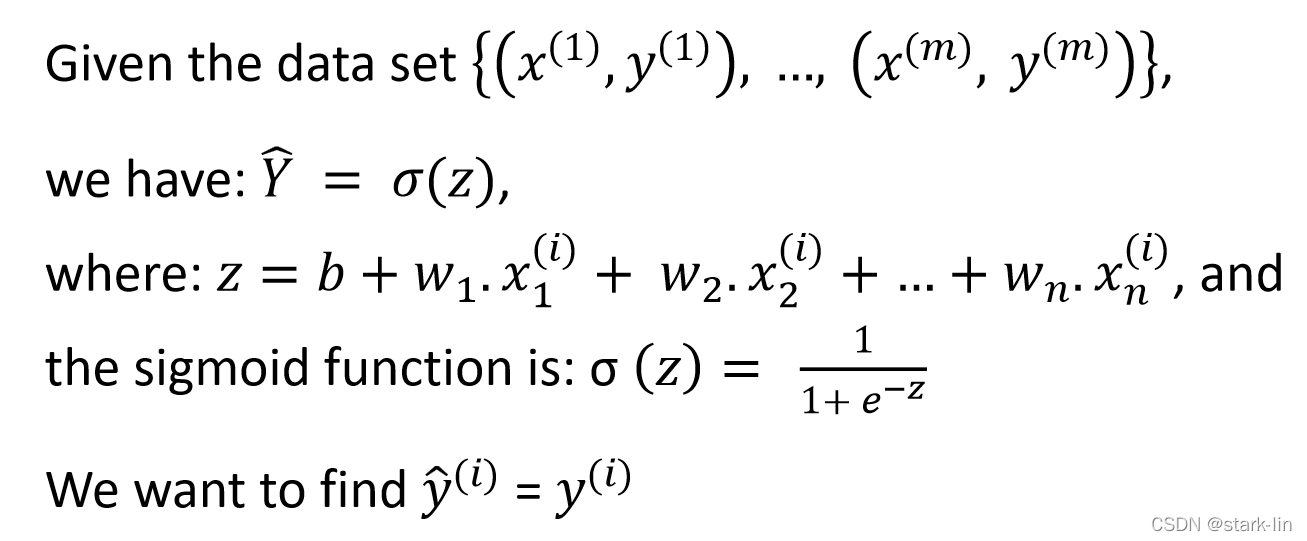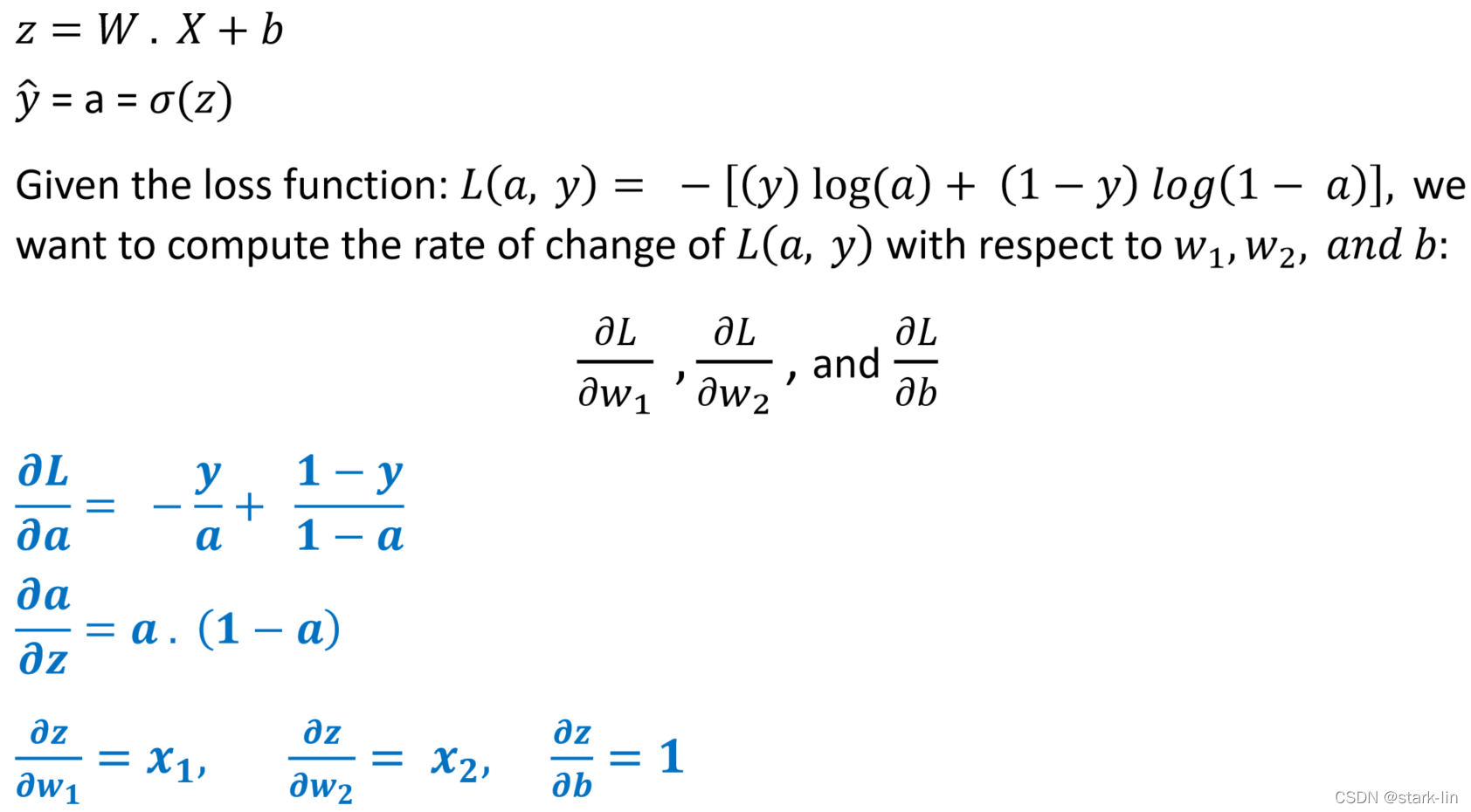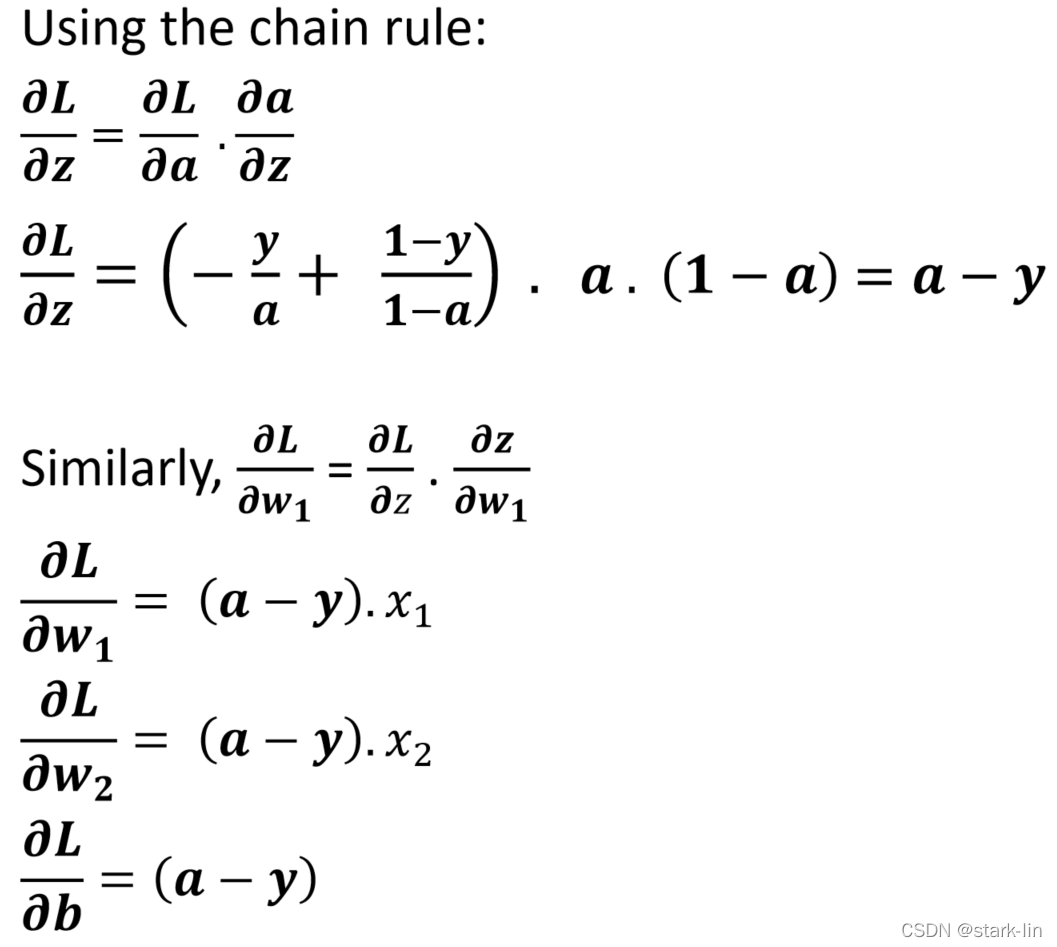神经网络（一）

文章目录

前言
一、神经网络结构
二、神经网络VS逻辑门
三、神经网络推导
- 3.1数学推导
- 3.2总结
四、numpy实现神经网络
总结

前言

老师：人是地球上最聪明的个体吗？
小明：是的？
老师：确定？
小明：手机，计算机…？我感觉它们要比我们厉害。
上述问答纯属虚构，如果某一天这个场景出现在小学课堂上，并且小明最后的回答是肯定的，那我们可能真正来到了强人工智能或者超人工智能时代。
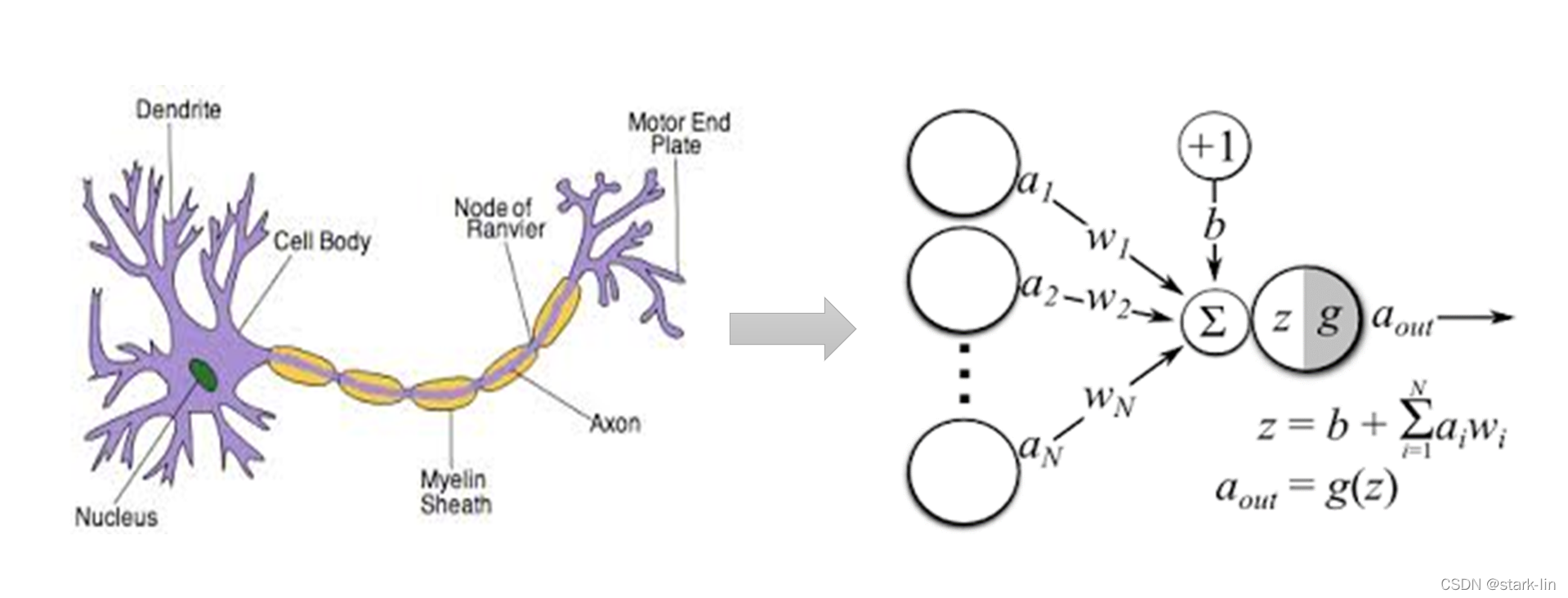
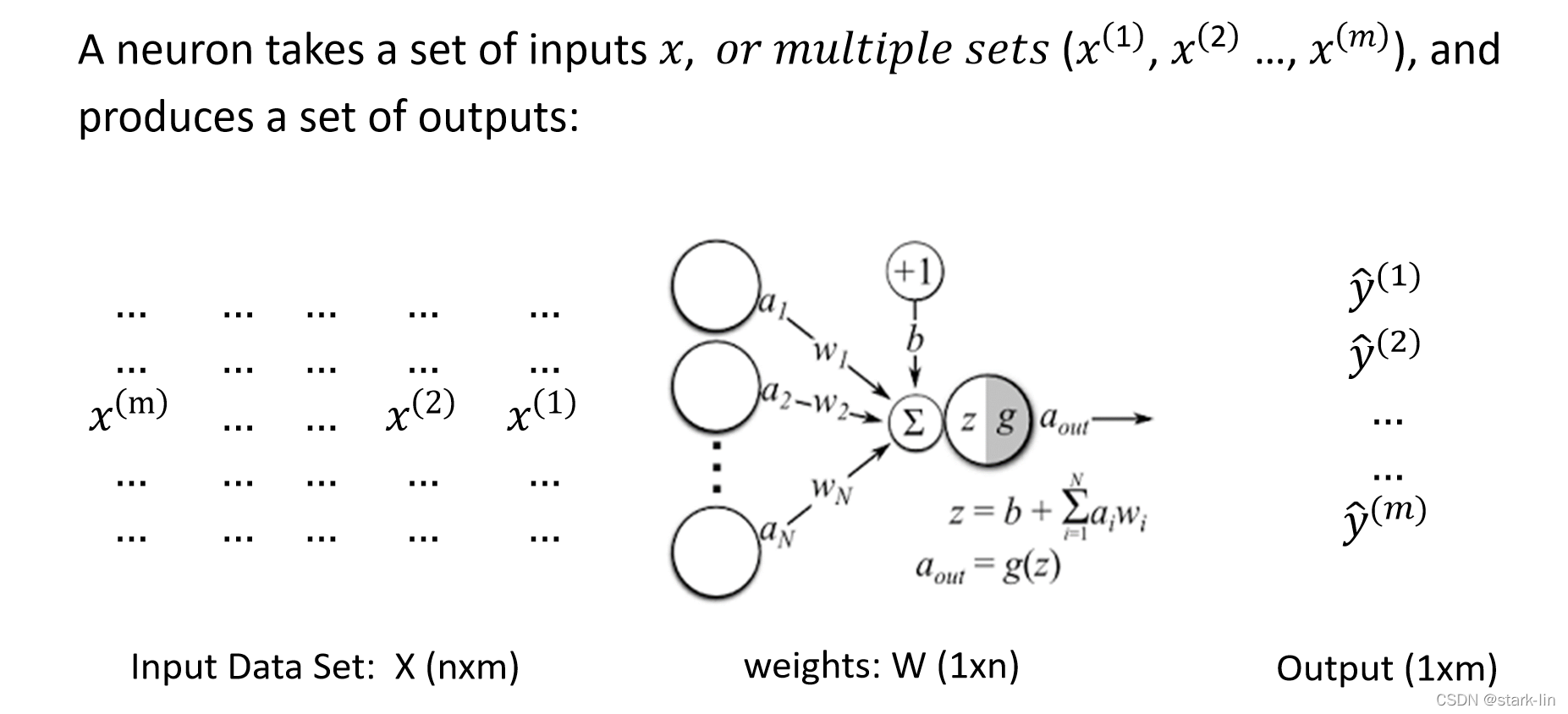
人之所以是最聪明的个体，是因为有一颗结构复杂的大脑，内部集成了上百亿的神经元，这些神经元组成某种结构并以某种机制实现了我们保存知识的能力和学习知识的能力，这里的保存知识，学习知识可以和计算机的存储、计算类比过来。
为什么小明会觉得手机和计算机要比我们人类厉害，就是因为计算机的计算能力，数据存储的持久能力都比人类厉害，一旦计算机掌握了人类的思维，那它的综合能力将会超越人类。不仅小明是这样想的，很多科学家也在研究人类的思维，从人类大脑最基本的组成单位神经元开始着手，用计算机去模拟一套人类的思维方式——人工神经网络（Artificial Neural Networks，ANNs）也简称为神经网络（Neural Networks，NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。

在这里插入图片描述

图1. 神经网络数学模型

一、神经网络结构

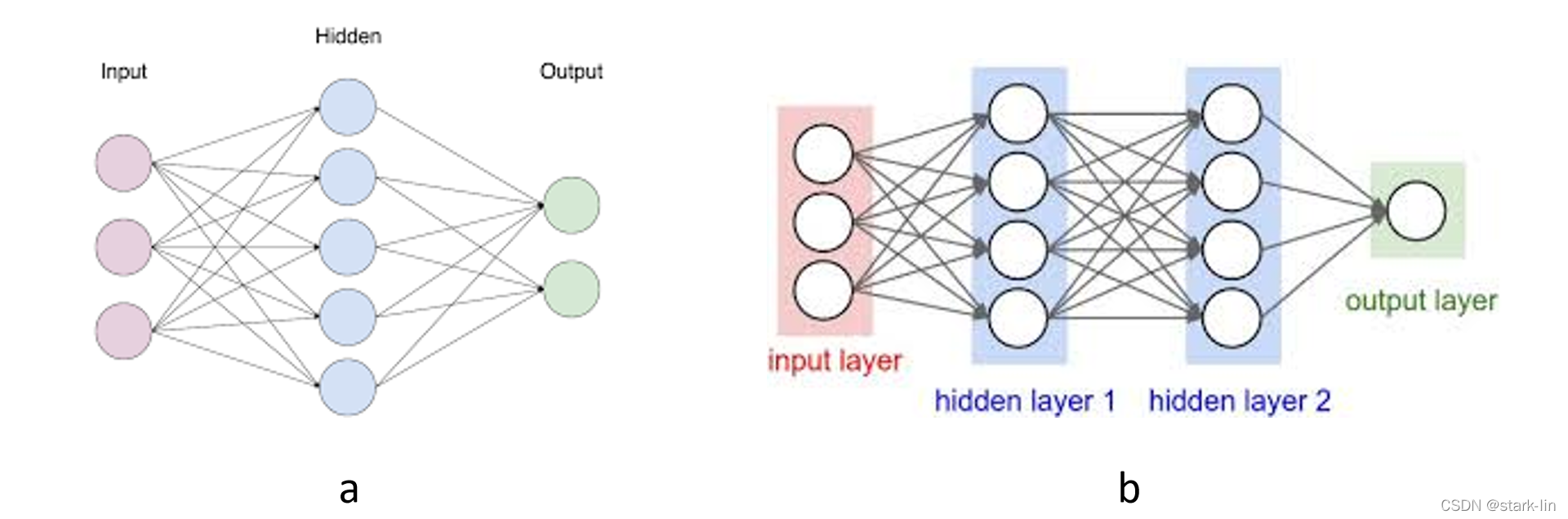
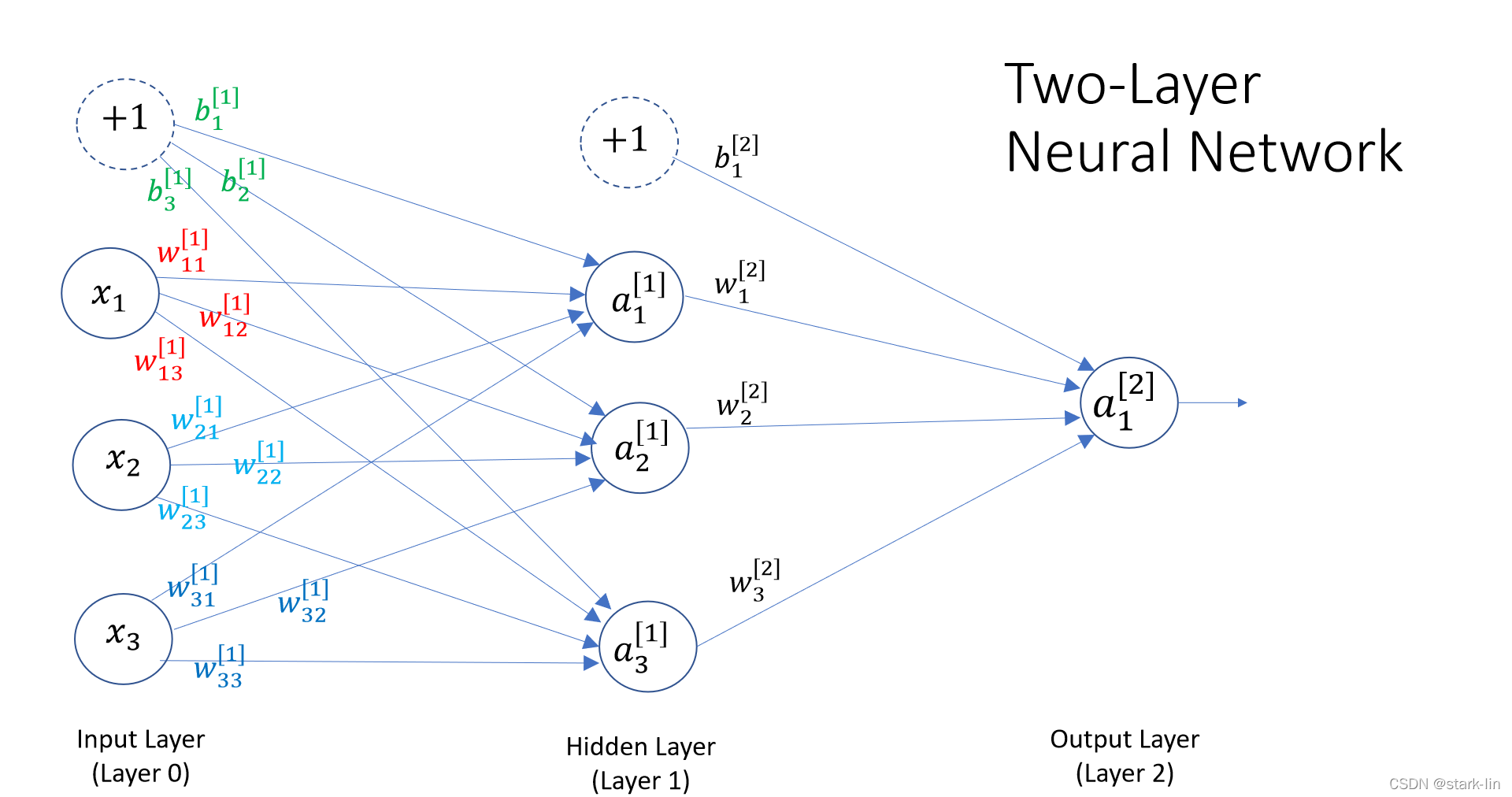
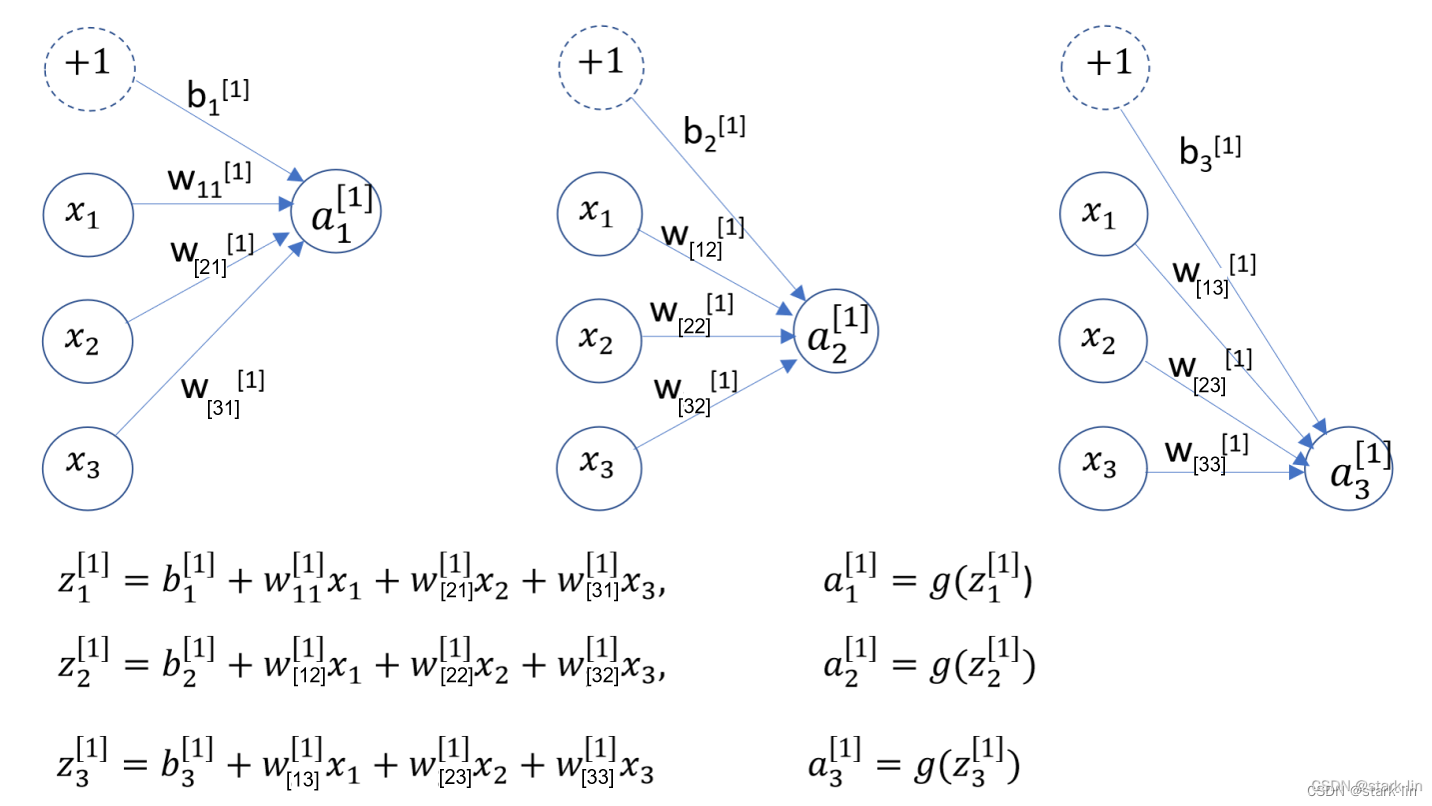
一般的神经网络包括输入层（Input Layer）、隐藏层（Hidden Layer）、输出层（Output Layer），层数大于等于2的神经网络称为多层神经网络（Multi-Layer Neural Network），一般是在隐藏层进行扩展。如图2中a是最基本的2层结构神经网络，b是在a的基础上对隐藏层进行扩展，变成3层神经网络。
注意：输入层不算。
在这里插入图片描述

图2. 多层神经网络

二、神经网络VS逻辑门

2.1 逻辑门

人类比较擅长模拟信号的处理，比如我们知道今天天气是34.5℃，比昨天的33℃要热一点，所以我们会考虑比昨天少穿衣服出门。这一过程涉及到模拟信号的处理（34.5大于33），也涉及到数字信号的处理（少穿衣服）。我们首先是通过模拟信号去处理信息，然后再进行数字信号的处理。怎么去模拟这一过程呢？神经网络现在可以闪亮登场了。
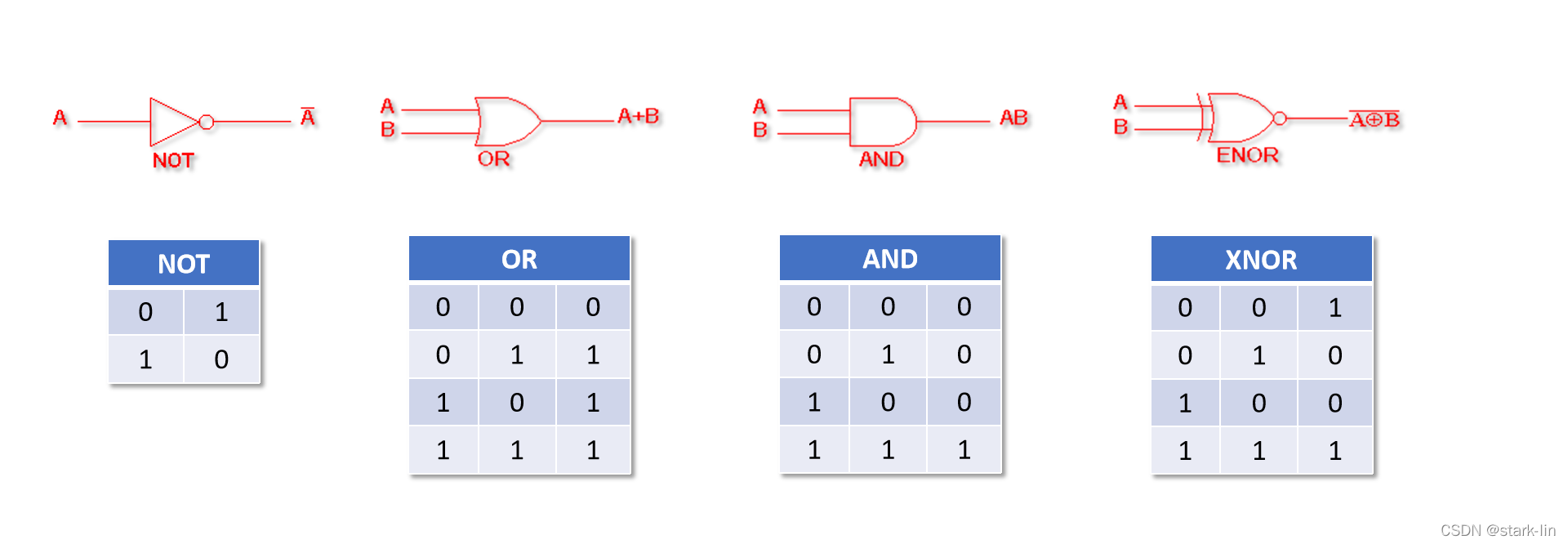
常见的逻辑门如下：
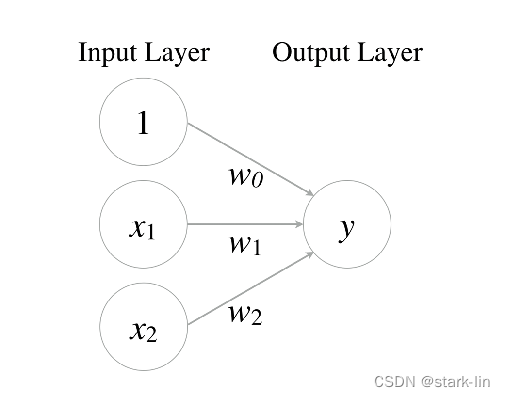
在这里插入图片描述

图3. 逻辑门符号及真值表

2.2 神经网络表示与门

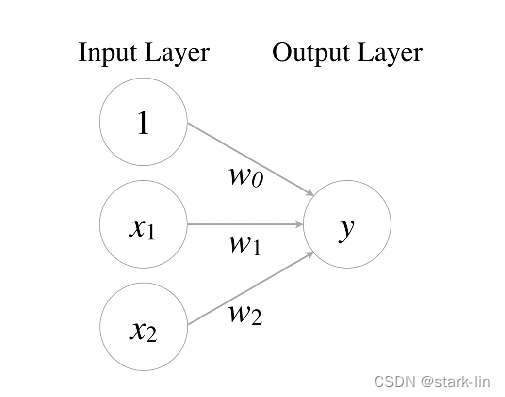
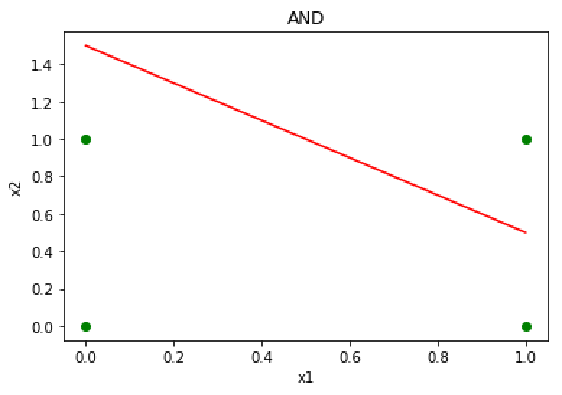
还是以一个简单的例子说明：期末到了，老师根据学生的数学、语文，还有平时的表现来决定颁发三好学生的奖状。老师看中的是学生平时的表现，很注重学生的人品，先学会做人，然后学会做事。学会做人是老师基本的要求，所以做得不好会扣0~30分，然后老师根据学生的数学、语文期末成绩进行评定，数学>80分，评分20分（w₁=+20），语文>80分，评分20分（w₂=+20）。
现在到了给小明评定的时候，小明属于那种调皮，但是很聪明的学生，经常给老师惹事儿，所以给了小明平时表现扣30分的标准（w₀=-30），让小明不那么容易拿到三好学生奖励（不容易激活）。小明本学期数学、语文期末成绩都是98。所以小明综合评定的结果是:-30 + 1 x (+20) + 1 x (+20) = +10。因为+10 > 0（激活函数σ），评定的结果是大于0的，按照规则，只要综合评定的分数大于0，就应该给小明颁发三好学生奖状。你是小明一类的学生吗？

在这里插入图片描述

w₀	w₁	w₂
-30	+20	+20

表1. 与门参数值表

$x_1 \space AND \space x_2 \space =σ(w_0 +w_1.x_1+w_2.x_2) \\ x_1, x_2\in\{0，1\} \tag1$

x₁	x₂	y	σ
0	0	0	g(-30)≈0
1	0	0	g(-10)≈0
0	1	0	g(-10)≈0
1	1	1	g(+10)≈1

表2. 与门真值表

我们使用神经网络并根据公式（1）实现了与门的功能，具体功能如表2与门真值表所示。

在这里插入图片描述

2.3 神经网络表示或门

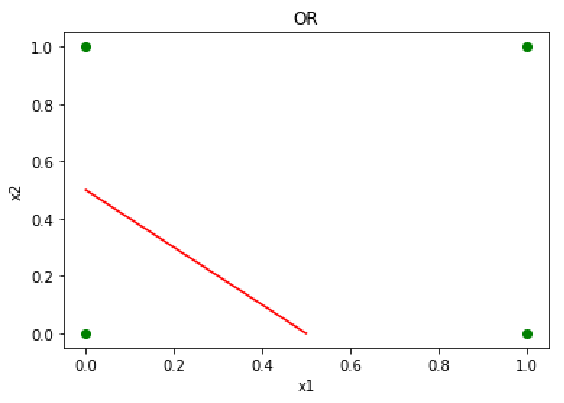
老师想了想，如果都以小明的标准去要求其他同学，是不是有点过分?毕竟调皮但是聪明的孩子只是个例，所以老师降低了平时考核的比重（w₀=-10），使得其他同学更容易拿到三好学生奖状（容易激活）。数学、语文的期末成绩还是一样的考核标准。
在这里插入图片描述

w₀	w₁	w₂
-10	+20	+20

表3. 或门参数值表

$x_1 \space OR \space x_2 \space =σ(w_0 +w_1.x_1+w_2.x_2) \\ x_1, x_2\in\{0，1\}\tag2$

x₁	x₂	y	σ
0	0	0	g(-10)≈0
0	1	1	g(+10)≈1
1	0	1	g(+10)≈1
1	1	1	g(+30)≈1

表4. 或门真值表

我们使用神经网络实现了或门的功能，只是改变了w₀的值，由原来的与门变成了现在的或门。老师的目的达到了，让更多的学生拿奖，只要学生的数学或语文成绩超过80分，就可以获得三好学生奖状。具体功能如表4或门真值表所示。

在这里插入图片描述

2.4 神经网络表示非门

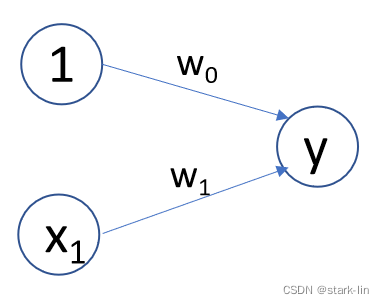
老师又想了想，不管表现好不好，一上来就扣掉30或者10分显然是不合理（w₀=-30/w₀=-10），人家班长小王平时表现这么好，没有奖励反倒是扣分，不合理，不合理！因为大多数同学都是很乖的，于是把平时表现这一块单独拿出来进行评定，平时分10分（w₀=+10），做的不好的才给与扣分（w₁=-20）。
到了给班长小王打平时成绩的时候了，小王因为是班长，所以扣分是不存在的，评分结果：+10 + 0 x (-20) = +10 > 0，所以结果显示，就平时成绩这一块，小王是没有问题的。那小明的情况呢？不容乐观。
在这里插入图片描述

w₀	w₁
+10	-20

表5. 非门参数值表

$NOT(x_1) \ =σ(w_0 +w_1.x_1)\\ x_1\in\{0，1\}\tag3$

x₁	y	σ
0	1	g(+10)≈1
1	0	g(-10)≈0

表6. 非门真值表

我们使用神经网络实现了非门的功能，只是改变了w₀，w₁的值，并且减少了一个神经元。

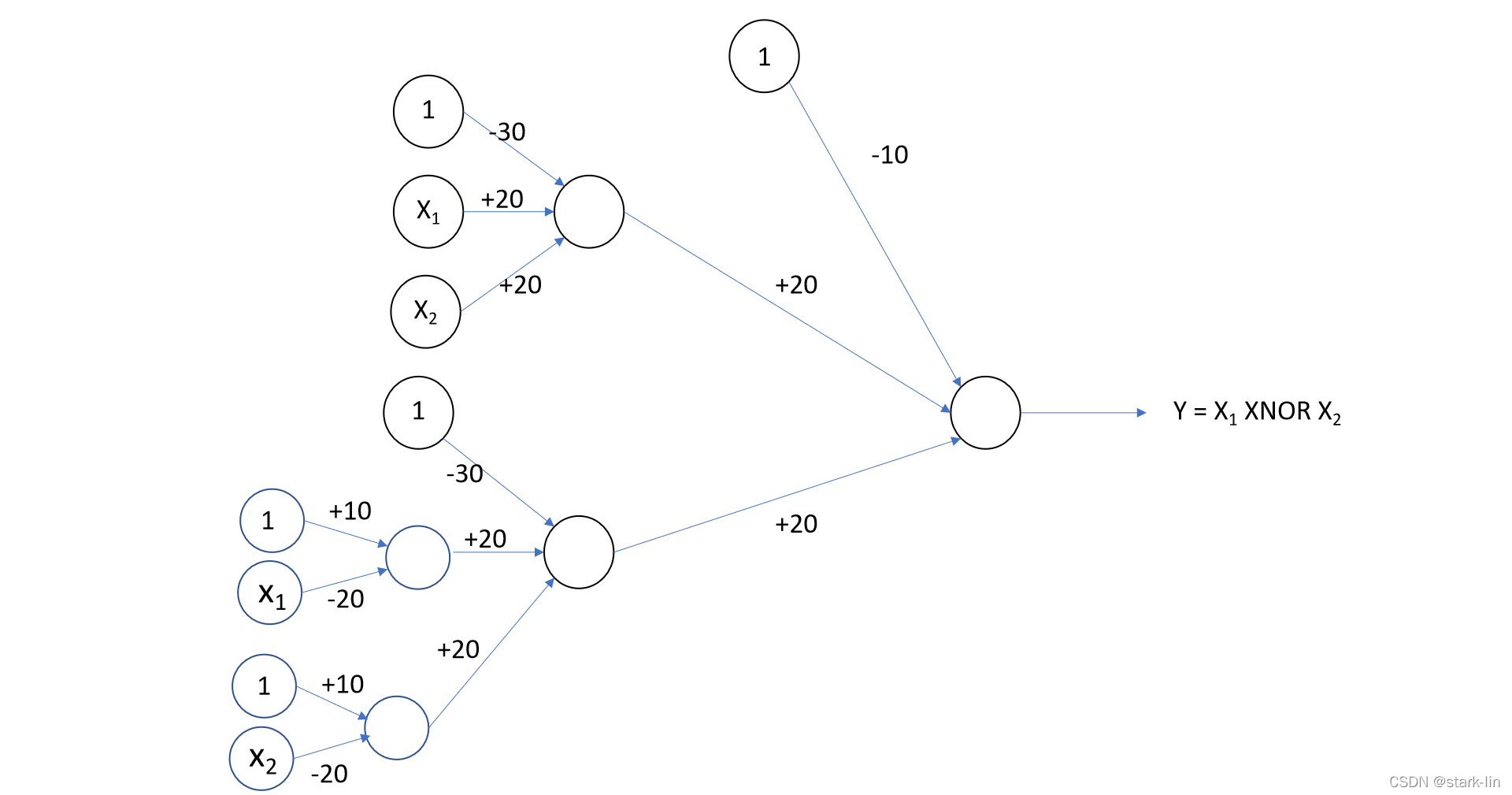
2.5 神经网络表示同或门

同或门其实就是前面的与门、或门、非门组成的，实现的方式是前面的神经网络组合连接。如公式4所示，有AND、OR、NOT。
在这里插入图片描述
$(x_1 \space AND \space x_2 )\space OR\space[NOT(x_1) \space AND \space NOT(x_2)] \\ x_1, x_2\in\{0，1\}\tag4$

x₁	x₂	x₁ and x₂	not(x₁) and not(x₂)	y
0	0	0	1	1
0	1	0	0	0
1	0	0	0	0
1	1	1	0	1

表7. 同或门真值表

神经网络的优势就是把我们复杂的日常转化为计算机擅长处理的逻辑表达，我们也知道FPGA中最基本的组成单元就是这些逻辑门。
tips:你也可以使用FPGA去实现神经网络。

三、神经网络推导

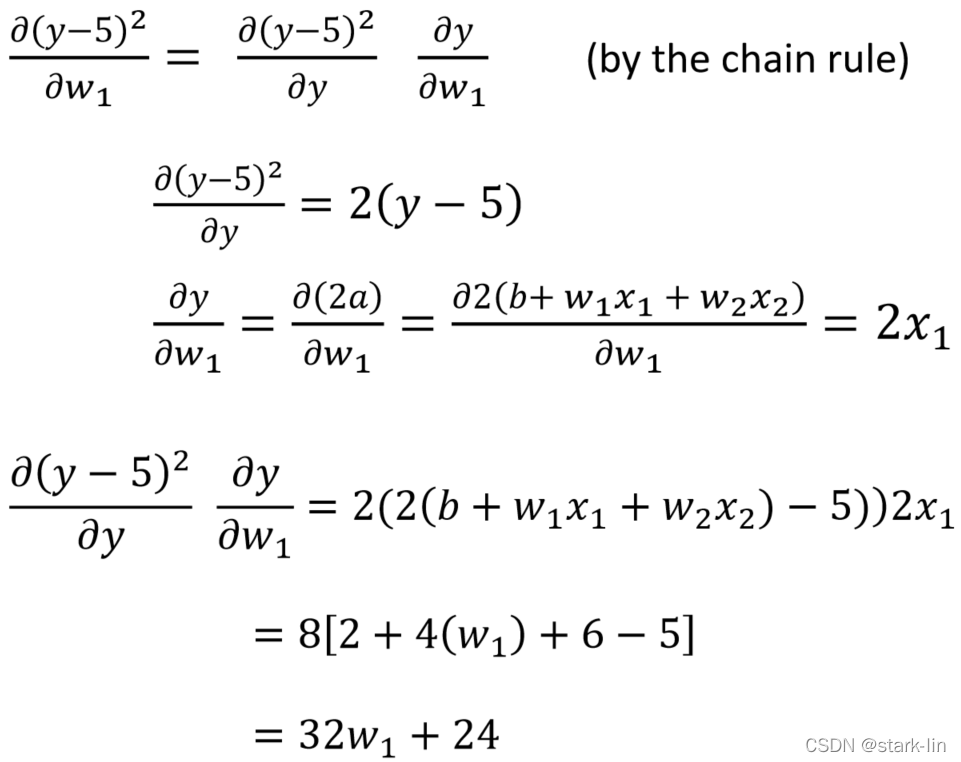
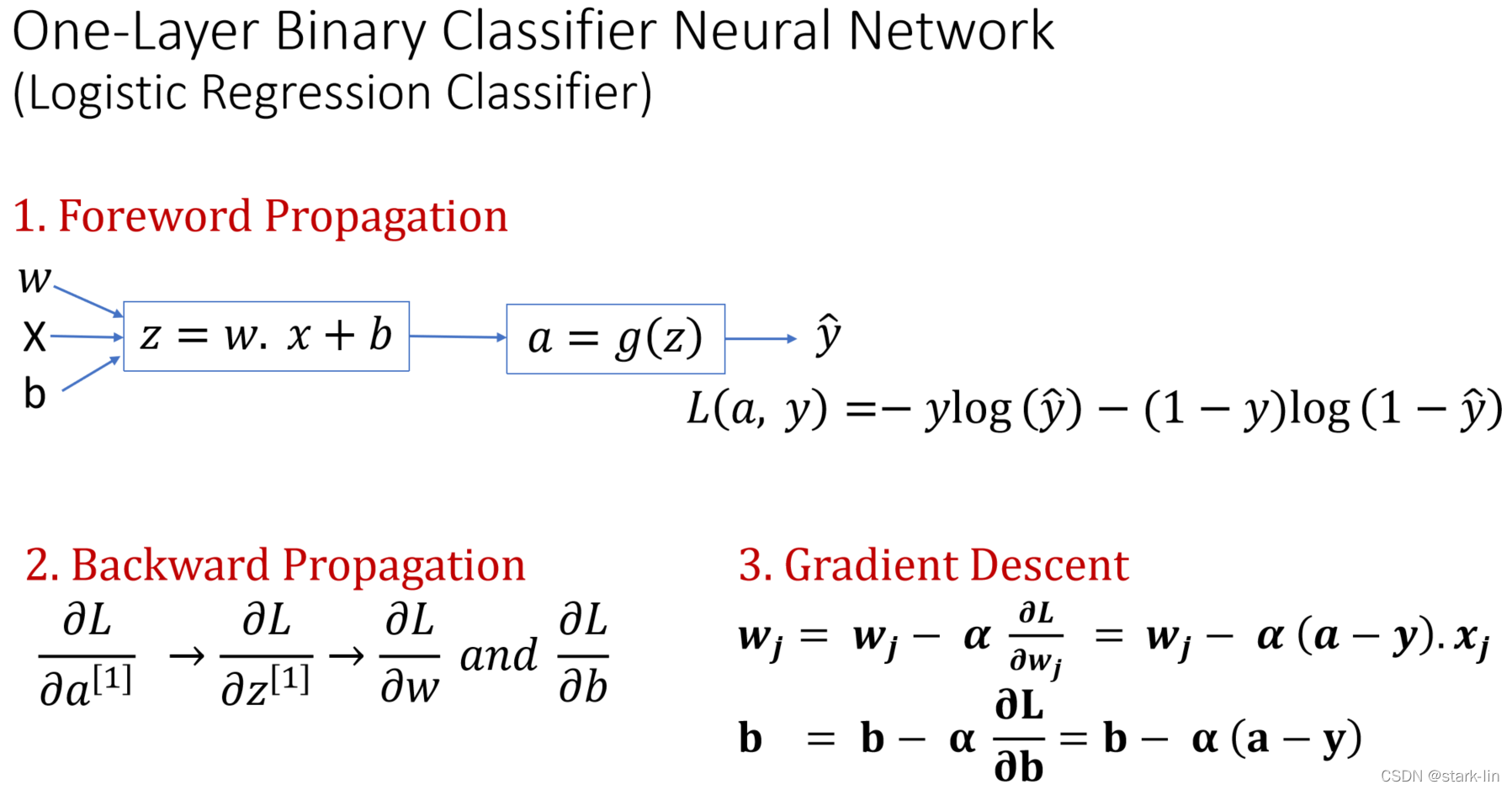
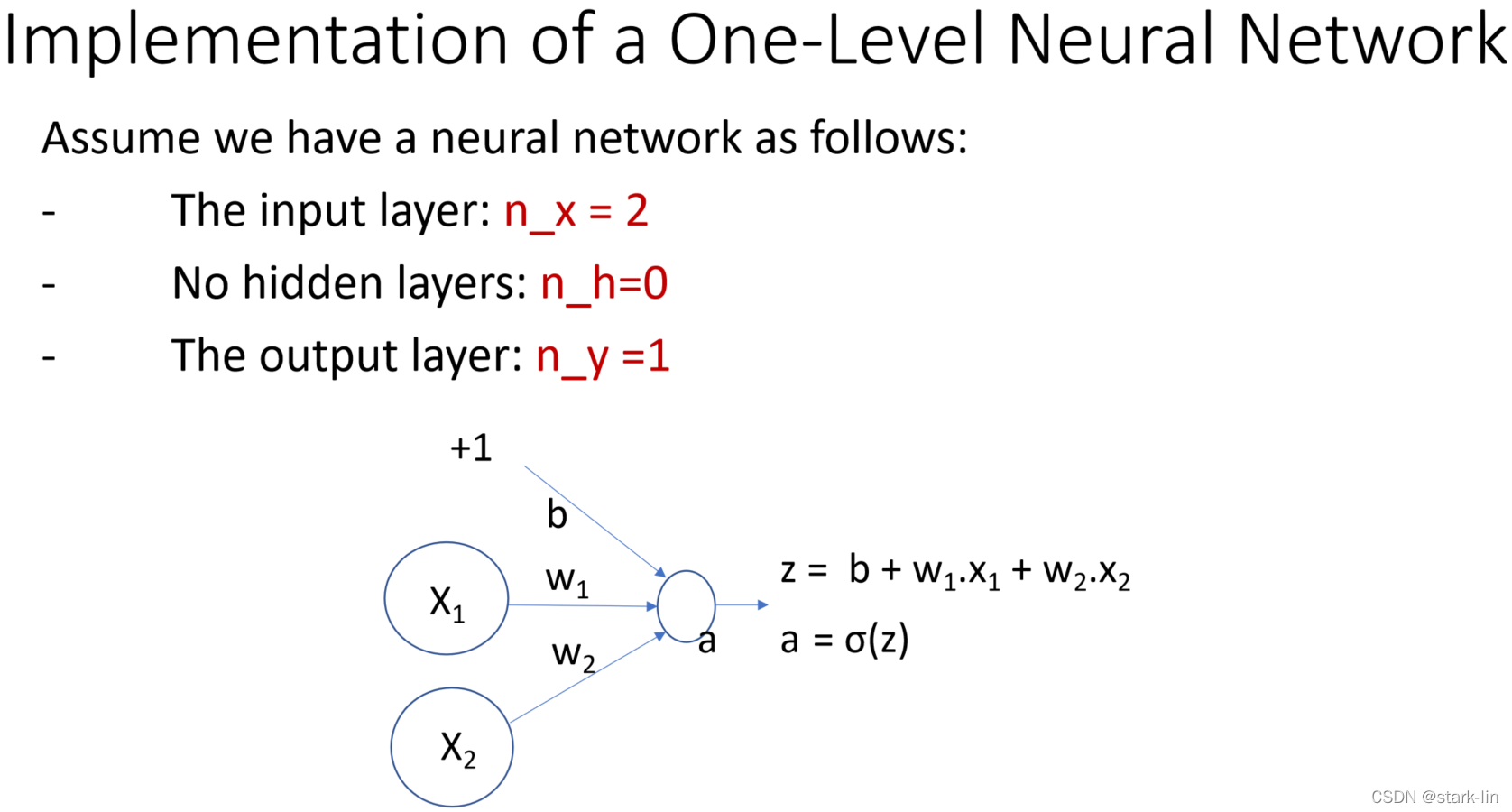
3.1数学推导

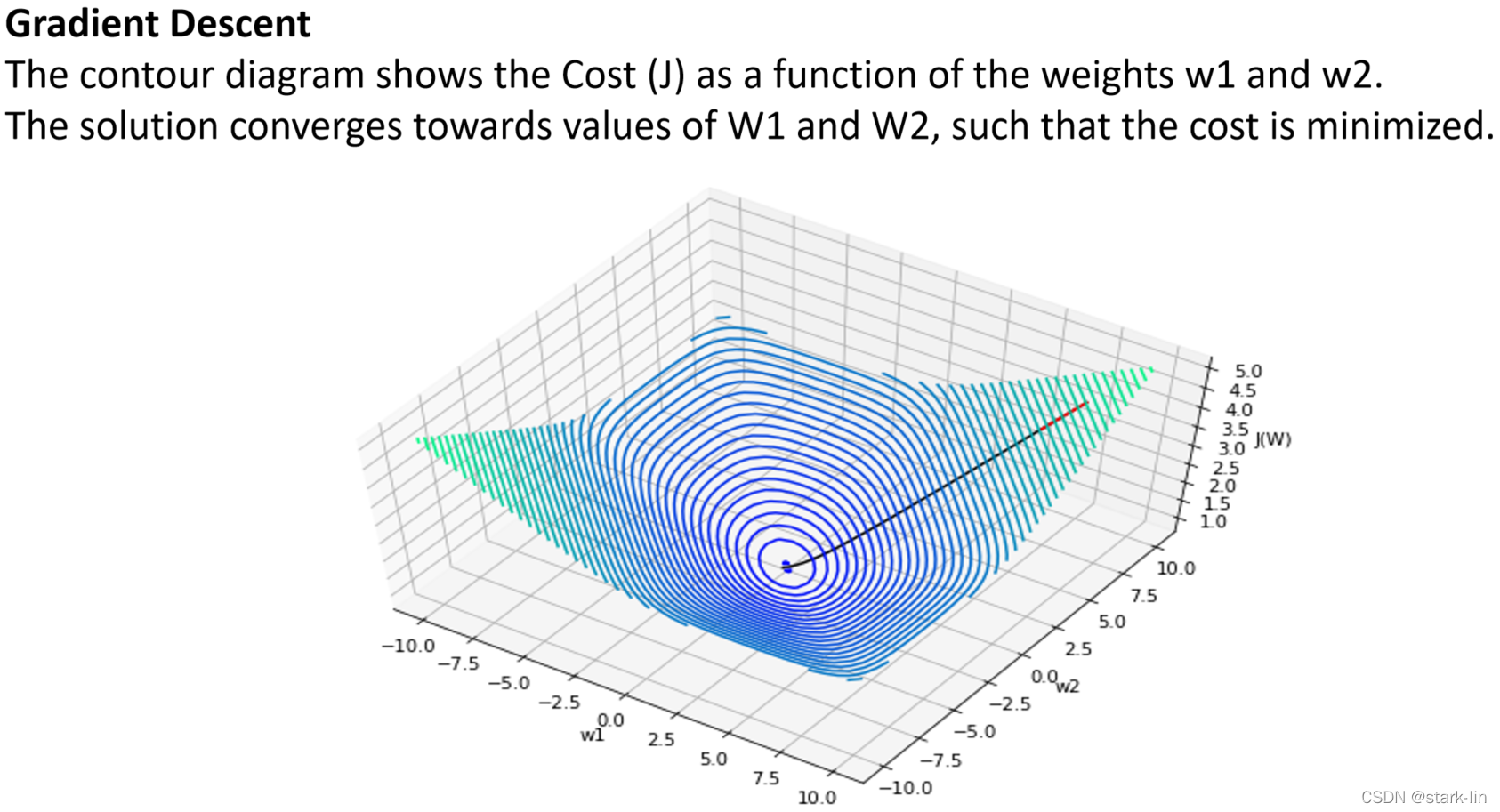
在这里插入图片描述

3.2总结

在这里插入图片描述

w1 = 1
w2 = 1
b = 1
x1 = 2
x2 = 3
y_pred = 8 + 4*w1
print('y_pred=', y_pred)
for i in range(20):
    dw1 = 24 + 32*w1
    w1 = w1 - 0.01*dw1
    y_pred = 8 + 4*w1 
    L = (y_pred - 5)**2
    print("L=", round(L,2), " 	y_pred=",round(y_pred,2), " 	w1=",round(w1,2), "dw1=", 	round(dw1,2))

在这里插入图片描述

四、numpy实现神经网络

在这里插入图片描述

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def sigmoid(z):
    return 1/(1+np.exp(-z))
def nn(X, y, m, alpha, num_of_iterations):
    b=0
    w = np.random.randn(1, X.shape[0]) * 0.01
    for iteration in range(num_of_iterations):
        J=0; dw1=0; dw2=0; db=0;
        for i in range(m):
            z = np.dot(w, X[:, i]) + b
            a = sigmoid(z)
            J += - (y[0,i]*np.log(a) + (1-y[0,i])*np.log(1-a))
            dz = a - y[0,i]
            dw1 += dz * X[0, i]
            dw2 += dz * X[1, i]
            db = db + dz
        J = J / m	
        dw1 = dw1 / m
        dw2 = dw2 / m
        db = db / m
        w[0,0] = w[0,0] - alpha * dw1
        w[0,1] = w[0,1] - alpha * dw2
        b = b - alpha * db
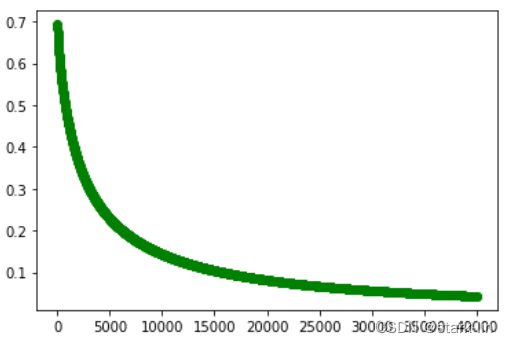
        if iteration%15 == 0:
            plt.plot(iteration, J, 'go')
    return b, w

X = np.array([[0,0], [0,1], [1,0], [1,1]]).T # The AND Operator, X is 2x4
y = np.array([[0,0,0,1]]) # y is 1x4
m = len(y[0])
alpha = 0.01
num_of_iterations = 40000
bias, w = nn(X, y, m, alpha, num_of_iterations)
print(bias, w[0,0], w[0,1])
fig = plt.figure()
plt.clf()

在这里插入图片描述

总结

以上就是神经网络基础知识、数学推导、以及numpy代码实现，懂了原理过后就可以使用一些流行的框架，比如tensorflow、pytorch、paddlepaddle进行快乐的人工智能探索了。人工智能时代，比的是谁先找到终极算法，可能是神经网络，也可能不是。