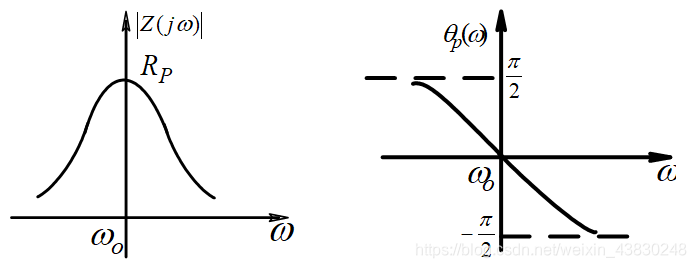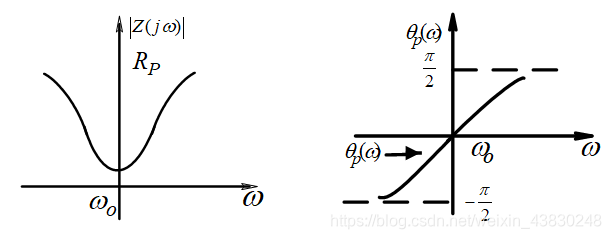作者：BerenCamlost

1 LC谐振电路

1.1 串并联谐振回路

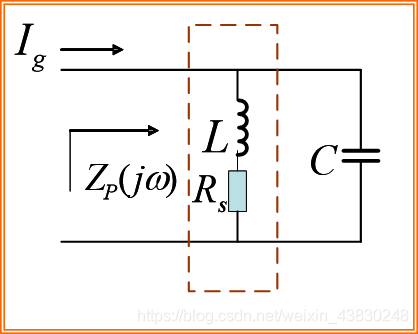
1.1.1 并联谐振回路

• 阻抗：
  $$Z_p(j\omega )=\frac{V_0(j\omega )}{I_g(j\omega )}$$
• 这个电路还可以等效成：
  
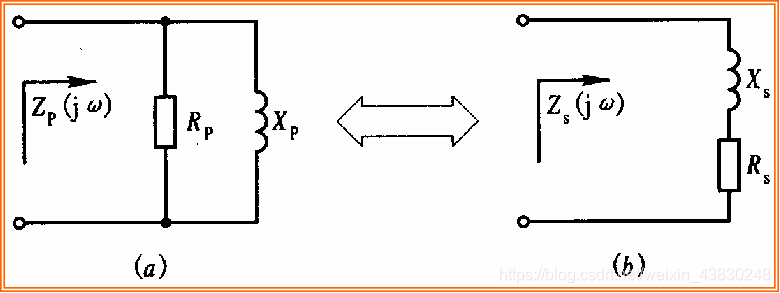
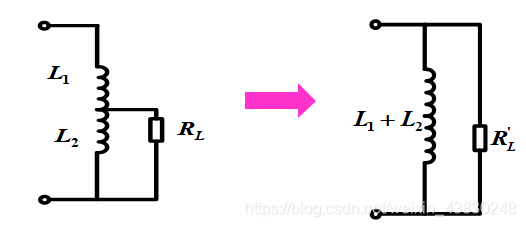
• 在基于保持其等效阻抗和Ｑ值不变的情况下，满足如下关系：
  $$Rp\approx Q^{2}Rs；Xp\approx Xs$$

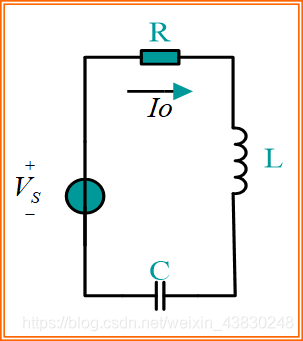
1.1.2 串联谐振回路

• 其阻抗和并联谐振回路正好互为倒数，为：
  $$Z_p(j\omega )=\frac{I_o(j\omega )}{V_g(j\omega )}$$

1.2 谐振角频率ωo

1. 回路无阻尼振荡角频率：
   $${\omega }_0=\frac{1}{\sqrt{LC}}$$
2. 谐振角频率可近似为ωo

1.3 有载品质因数

1. 串联与并联回路Q值相同，可以用下列公式计算：
   $$Q=\frac{{\omega }_{0}L}{R_s}=\frac{1}{{\omega }_{0}C{R}_s}={\omega }_{0}C{R}_p=\frac{R_p}{{\omega }_{0}L}$$
2. 如果Q不考虑电容的损耗（Rs），就等于电感的固有Q
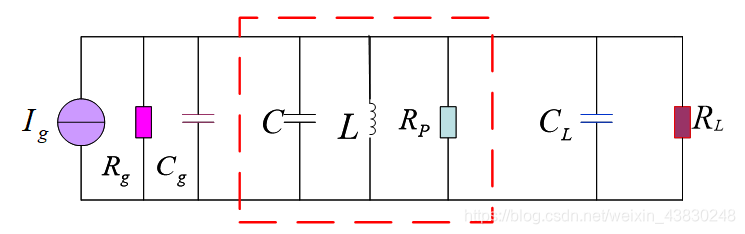
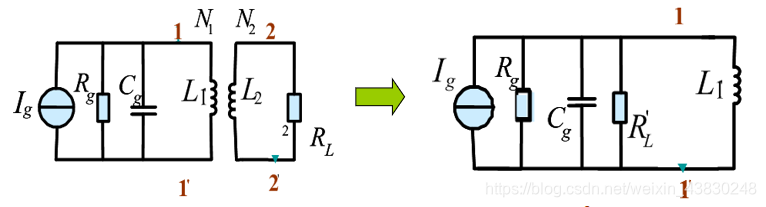
3. 在加入信号源和负载的情况下，如下图所示：
   
   此时得到的有载品质因数的计算公式：
   $$Q_e=\frac{R_{\Sigma }}{{\omega }_{0}L}$$
   其中：
   $$C_{\Sigma }=C_g+C+C_L，R_{\Sigma }=R_p//R_g//R_L$$

1.4 串并联回路的阻抗特性

1. 并联回路
   
   如上两图所示，可以知道，并联谐振时，输出电压最大。
   另外，
   ω = 0 ，呈纯电阻且阻值最大
   ω > 0 ，呈容性
   ω < 0 ，呈感性
   
2. 串联回路
   
   如上两图所示，可以知道，串联谐振时，输出电流最大。
   另外，
   ω = 0 ，呈纯电阻且阻值最小
   ω > 0 ，呈感性
   ω < 0 ，呈容性
   

1.5 通频带

1.5.1 Bw定义

当保持外加信号的幅值不变而改变其频率时, 将并联回路端电压值(串联回路电流值） 下降为谐振值的$1/\sqrt{2}$时对应的频率范围称为回路的通频带。

1.5.2 计算公式

$$BW=2\Delta f=\frac{f_0}{Q}$$
加入负载后，BW变大，选频特性变差

1.6 阻抗变化的计算

1.6.1变压器耦合电路

$$P=\frac{V_2}{V_1}=\frac{N_2}{N_1}<1，R_L^{\prime }=\frac{1}{p^2}{R}_L$$

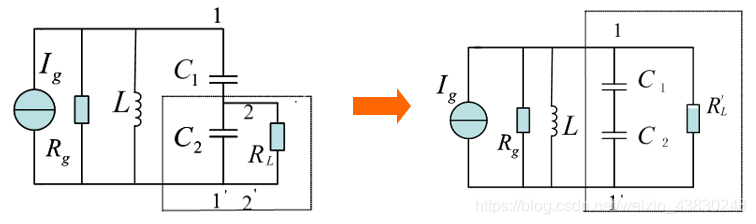
1.6.2 双电容耦合回路

• 利用部分接入法实现的双电容耦合回路，其接入系数和等效阻抗为
  $$P=\frac{V_2}{V_1}=\frac{C_1}{C_1+C_2}，R_L^{\prime }=\frac{1}{p^2}{R}_L$$

1.6.3 双电感耦合回路

• 利用部分接入法实现的双电感耦合回路，其接入系数和等效阻抗为
  $$P=\frac{V_2}{V_1}=\frac{L_2}{L_1+L_2}，R_L^{\prime }=\frac{1}{p^2}{R}_L$$
  注意电感和电容回路公式的区别

2 表面波滤波器（SAW）

2.1 基本原理

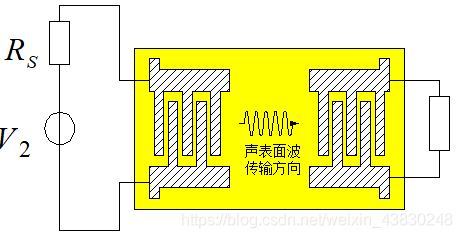
• 声表面波滤波器是一种以铌酸锂、锆钛酸铅或石英等压电材料为基体构成的一种电声换能元件。
• 转换过程：

• 其信号转换示意图：

2.2 声表面波（SAW）滤波器的特点

• 体积小、重量轻。
• 中心频率可达几MHz～几GHz，适合于高频、超高频工作。幅频特性接近理想矩形。
• 相对通频带有时可以达到50%，频率特性取决于压电基体材料及叉指换能器的指条数目、疏密和长度。
• 用与集成电路相同的平面加工工艺。制造简单、重复性好

3 电阻热噪声

3.1 热噪声电压和功率谱密度

1. 热噪声电压（奈奎斯特公式）
   $$\overline{{U_n}^2}=4kTBR$$

• 其中
  • K为玻耳兹曼常数 $=1.38\times 10^{-23}J/K$
  • T热力学温度，一般为290
  • R为电阻器的电阻值
  • B为测量带宽

2. 功率谱密度
   $$S_U=4kTR(V^2/Hz)$$

3.2 电阻器噪声额定功率

3.3 等效噪声带宽

$$U_{n2}^2=4kTR{B}_n{H}_0^2\Rightarrow B_n=\frac{{\int }_0^{\infty }{\left|H(j\omega )\right|}^{2}df}{{H_0}^2}=\frac{\pi f_0}{2Q}=1.57B_{0.7}$$

• 其中$H_0$为$\left|H(j\omega )\right|$的最大值

4 噪声系数

4.1 噪声系数的定义

• 在标准信号源激励下，网络输入信噪比与其输出信噪比的比值。
  $$N_F=\frac{S_i/N_i}{S_o/N_o}$$

4.2 噪声系数的描述方法

1. 信噪比恶化程度
   $$N_F=\frac{S_i/N_i}{S_o/N_o}$$
2. 网络输出噪声功率和输入噪声功率在输出端的比值
   $$N_F=\frac{S_i/N_i}{S_o/N_o}=\frac{N_o}{(S_o/S_i)N_i}=\frac{N_o}{K_p{N}_i}$$

• 其中$K_p$为功率增益，网络输出与输入信号功率比值$K_p=S_o/S_i$

3. 任何实际网络的噪声系数，都是在理想网络噪声系数的基础上加上一个增量

• 由2中的公式可以导出
  $$N_o=K_p{N}_i+N_a$$
• 其中$N_a$：网络附加噪声的输出功率

所以有：
$$N_F=1+\frac{N_a}{K_p{N}_i}$$

4.3 无源网络噪声系数

$$N_F=\frac{1}{K_{pm}}=L$$

• 其中$K_{pm}=\frac{S_{mo}}{S_{mi}}$
• 其中L为网络的衰减
• 无源网络的噪声系数等于网络的衰减。产生网络噪声的有损元件，是导致网络传输信号衰减的因素。

4.4 级联网络噪声系数

$$N_F=N_{F1}+\frac{N_{F2}-1}{K_{pm1}}+\frac{N_{F3}-1}{K_{pm1}{K}_{pm2}}+\cdot \cdot \cdot +\frac{N_{FN}-1}{K_{pm1}\cdot \cdot \cdot K_{pm(n-1)}}$$

4.5 接收机的灵敏度

$$S_{i(min)}={\left(\frac{S_o}{N_o}\right)}_{min}{N}_{F}kT\Delta F$$

• $\Delta F$是等效噪声带宽

4.6 最小可检测信号电压

$$S_{i(min)}=\frac{{V_{S(min)}}^2}{4R_S}\Rightarrow V_{S(min)}=2\sqrt{R_S{S}_{i(min)}}$$