前言：今天碰到了一题关于滑动窗口+二分查找的题目，用C++做题时需要使用multiset，因此前来贴出模板，望能供大家参考。

题目

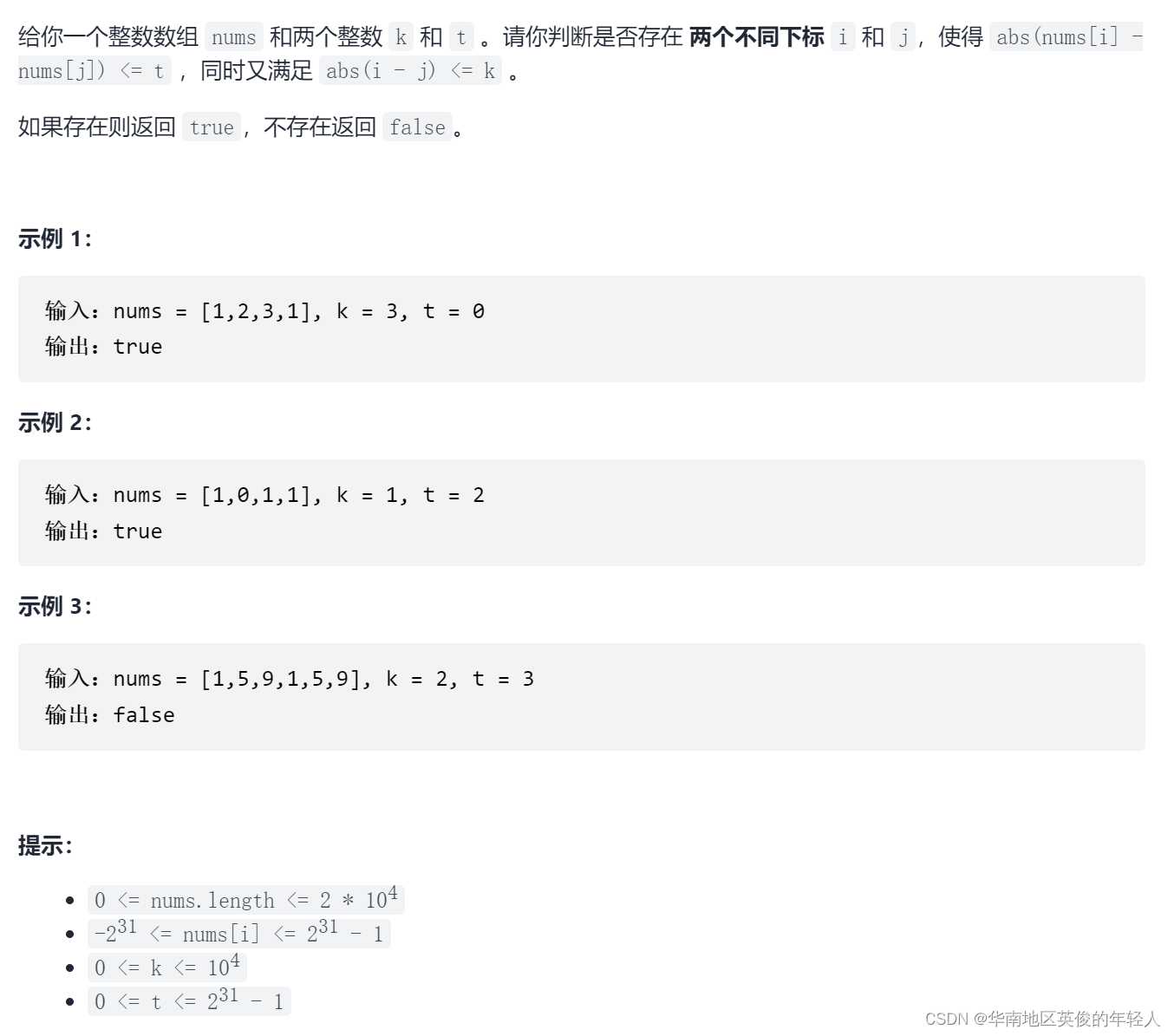
这里贴出原题：LC 220. 存在重复元素 III 供大家测试代码使用

题目解析: 本道题如果使用其他方法可能会将题目复杂化，但是如果使用滑动窗口却会非常直观：由于题目需要找两个下标不同的元素，所以我们可以将 $nums[0]$ 插入集合后，枚举窗口右边界的下标 $i(i\in [1,n-1])$，同时当集合大小超过上限 $k+1$ 后，抹除窗口左边界元素即可。

代码：

class Solution {
public:
    using LL = long long;
    
    bool containsNearbyAlmostDuplicate(vector<int>& nums, int w, int t) {
        if(w == 0)  return false;
        
        int n = nums.size();
        multiset<LL> s;
        
        s.insert(nums[0]);
        
        for(int i = 1; i < n; ++i){
            int v = nums[i];
            const auto& pos = s.lower_bound(v);
            
            if(pos != s.end() and abs(v - *pos) <= t)     return true;
            if(pos != s.begin() and abs(v - *(prev(pos, 1))) <= t)  return true;
                
            s.insert(v);
            if(i >= w){
                s.erase(s.find(nums[i - w]));
            }
        }
        
        return false;
    }
};

这里需要注意三点

• 需要使用 multiset 自带的二分查找库函数才能够保证 $O(logn)$ 的查找效率，使用 std 的二分查找库函数可能会导致查找效率退化至 $O(n)$，原因有可能是 multiset 不支持按照下标访问.
• 由于 multiset 不支持下标访问，所以访问前一个或者后一个迭代器的时候，可以使用 prev(pos, 1)/ next(pos, 1) 的方式，其中 pos 为红黑树迭代器.
• 由于 multiset 的 erase(x) 函数会删除所有值为x的节点，因此采用s.erase(s.find(x));可以保证只删除一个.

以上结论对于C++中的 set 一样适用. 收！

参考文章：关于C++ STL中对于set使用lower_bound进行二分查找的效率问题