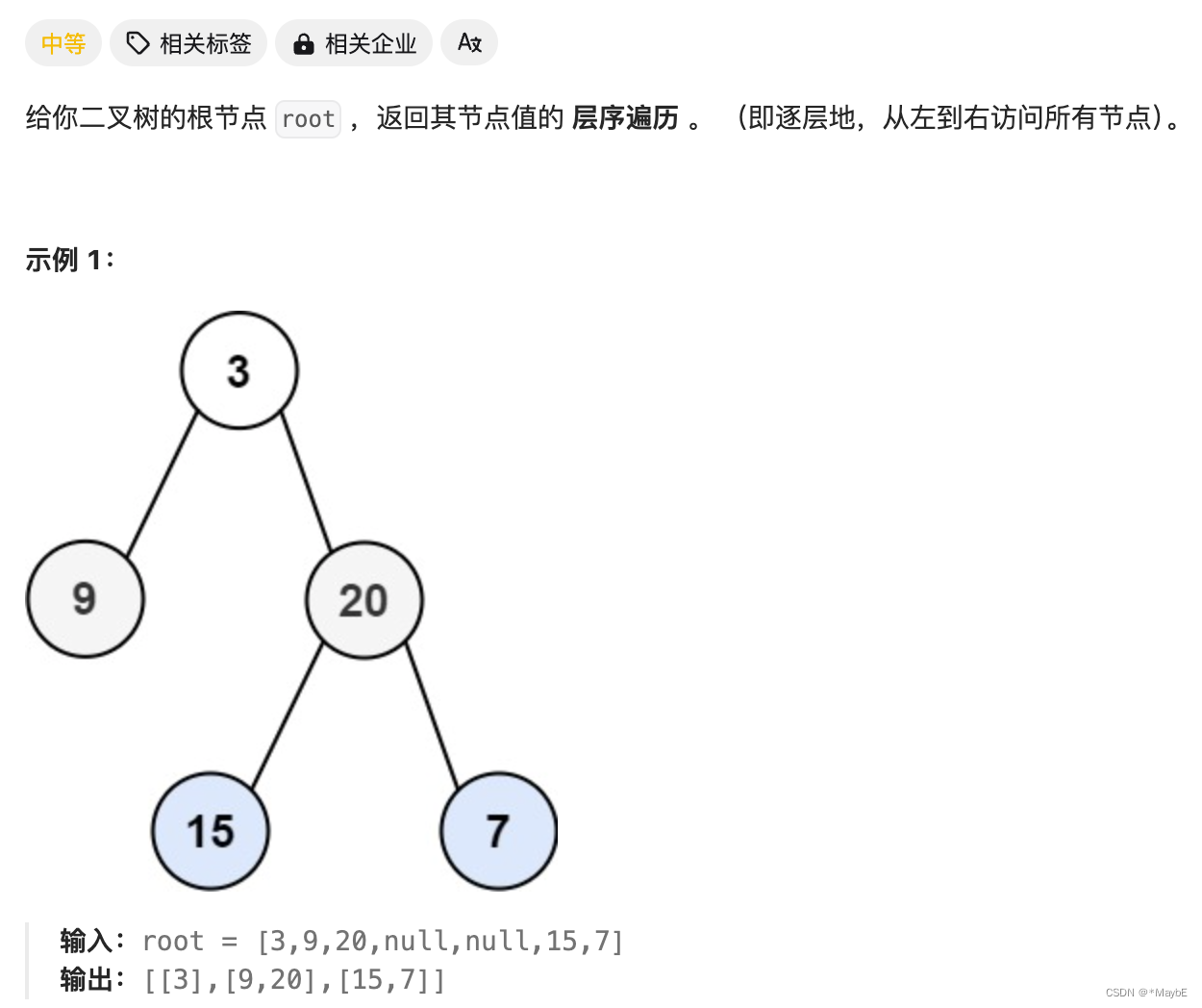
102. 二叉树的层序遍历

题目链接：102. 二叉树的层序遍历
文档讲解：代码随想录
状态：dfs没写出来，bfs不知道如何分层

import java.util.*;

public class BinaryTreeLevelOrderTraversal {
    // 用于存储每一层的节点值
    List<List<Integer>> res = new LinkedList<>();

    // 使用深度优先搜索 (DFS) 进行层序遍历
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root != null) {
            dfs(root, 0); // 从根节点开始，深度为0
        }
        return res;
    }

    // DFS辅助方法
    public void dfs(TreeNode root, int depth) {
        if (root == null) {
            return; // 如果当前节点为空，直接返回
        }
        if (res.size() == depth) {
            // 如果当前深度没有对应的列表，创建一个新的列表
            res.add(new ArrayList<>());
        }
        // 将当前节点的值添加到对应深度的列表中
        res.get(depth).add(root.val);
        // 递归处理左子节点，深度加1
        dfs(root.left, depth + 1);
        // 递归处理右子节点，深度加1
        dfs(root.right, depth + 1);
    }

    // 使用广度优先搜索 (BFS) 进行层序遍历
    public List<List<Integer>> bfs(TreeNode root) {
        Deque<TreeNode> queue = new LinkedList<>(); // 使用双端队列来存储节点
        if (root != null) {
            queue.addLast(root); // 将根节点加入队列
        }
        while (!queue.isEmpty()) {
            // 获取当前层的节点个数.
            // 重要!!!后面代码中利用size--处理掉每层的结点后,队列中剩下的结点就是下一层的结点
            int size = queue.size(); // 当前层的节点数
            ArrayList<Integer> list = new ArrayList<>(); // 用于存储当前层的节点值
            while (size > 0) {
                TreeNode node = queue.pollFirst(); // 取出当前层的节点
                list.add(node.val); // 将节点值加入当前层的列表
                if (node.left != null) {
                    queue.addLast(node.left); // 将左子节点加入队列
                }
                if (node.right != null) {
                    queue.addLast(node.right); // 将右子节点加入队列
                }
                size--;
            }
            res.add(list); // 将当前层的节点值列表加入结果列表
        }
        return res;
    }
}

// 定义树节点类
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

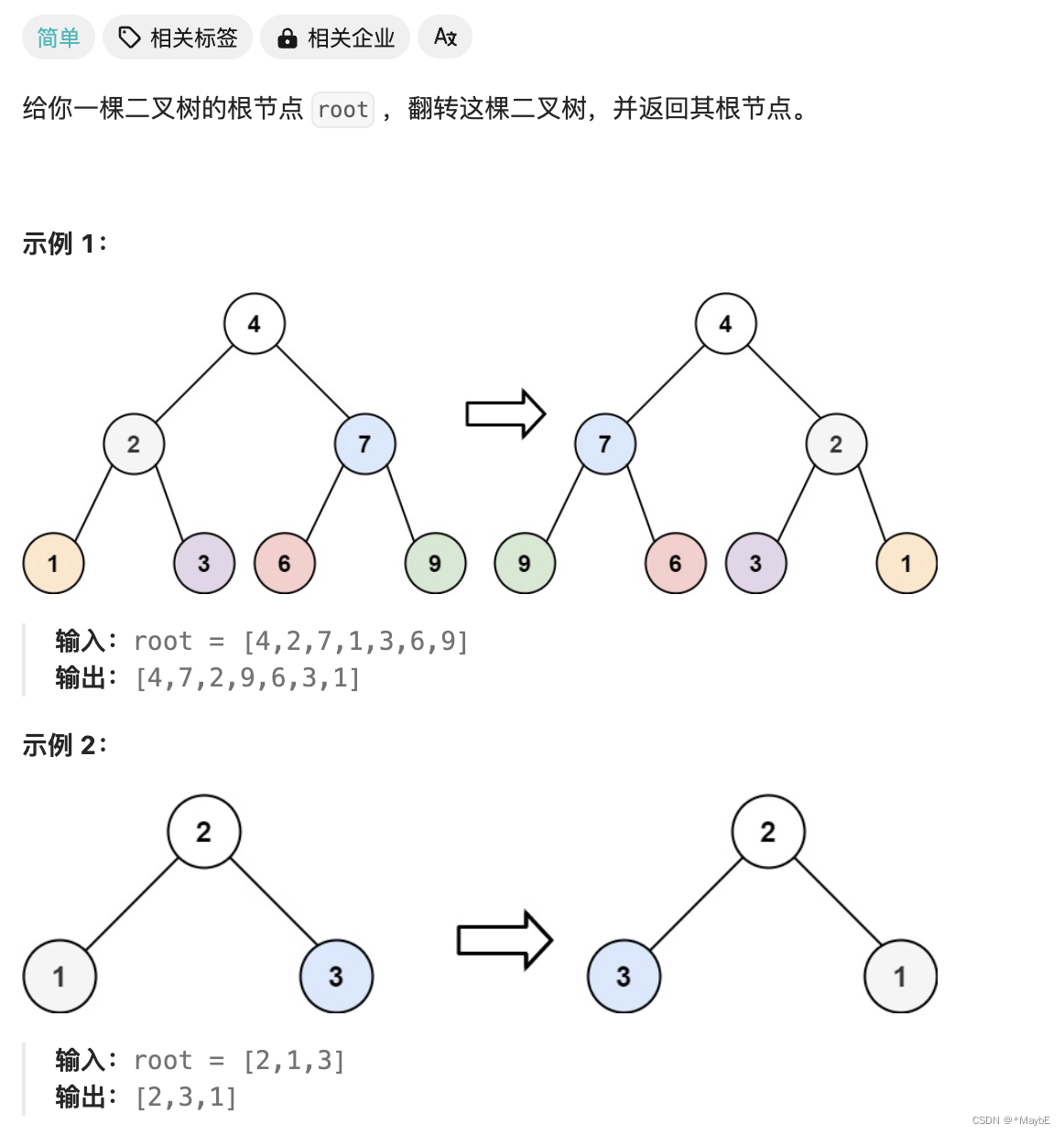
226.翻转二叉树

题目链接：226.翻转二叉树
文档讲解：代码随想录
状态：so easy

    // 使用递归方式进行二叉树翻转
    public TreeNode invertTree(TreeNode root) {
        if (root != null) {
            // 保存当前节点的左子节点
            TreeNode left = root.left;
            // 保存当前节点的右子节点
            TreeNode right = root.right;
            // 递归翻转右子树，并将其设为当前节点的左子节点
            root.left = invertTree(right);
            // 递归翻转左子树，并将其设为当前节点的右子节点
            root.right = invertTree(left);
        }
        // 返回翻转后的根节点
        return root;
    }

    // 使用广度优先搜索 (BFS) 进行二叉树翻转
    public TreeNode bfs(TreeNode root) {
        if (root != null) {
            // 创建一个双端队列来存储节点
            Deque<TreeNode> deque = new LinkedList<>();
            // 将根节点加入队列
            deque.addLast(root);
            // 当队列不为空时，继续处理
            while (!deque.isEmpty()) {
                int size = deque.size(); // 当前层的节点数
                // 遍历当前层的所有节点
                while (size-- > 0) {
                    // 取出当前层的节点
                    TreeNode node = deque.pollFirst();
                    // 翻转当前节点的左右子节点
                    TreeNode temp = node.left;
                    node.left = node.right;
                    node.right = temp;
                    // 如果左子节点不为空，将其加入队列
                    if (node.left != null) {
                        deque.add(node.left);
                    }
                    // 如果右子节点不为空，将其加入队列
                    if (node.right != null) {
                        deque.add(node.right);
                    }
                }
            }
        }
        // 返回翻转后的根节点
        return root;
    }

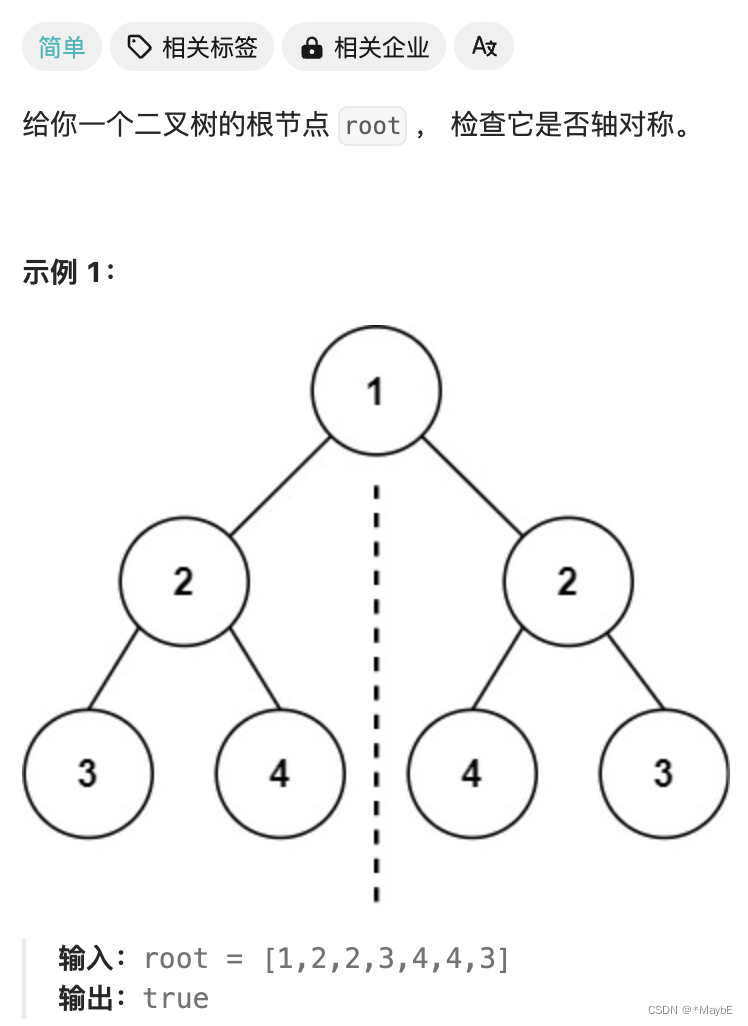
101. 对称二叉树

题目链接：101. 对称二叉树
文档讲解：代码随想录
状态：有思路，但是写代码一直卡着

    // 判断二叉树是否对称
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true; // 如果根节点为空，则认为是对称的
        }
        TreeNode left = root.left;
        TreeNode right = root.right;
        // 比较根节点的左右子树是否对称
        return compare(left, right);
    }

    // 辅助方法：比较两个子树是否对称
    public boolean compare(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true; // 如果两个子树都为空，则对称
        } else if (left == null || right == null) {
            return false; // 如果其中一个子树为空，则不对称
        } else {
            // 比较左子树的左子树与右子树的右子树，左子树的右子树与右子树的左子树，以及当前节点的值是否相等
            return compare(left.left, right.right) && compare(left.right, right.left) && left.val == right.val;
        }
    }

    public boolean isSymmetric(TreeNode root) {
        if (root == null || (root.left == null && root.right == null)) {
            return true;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        stack.addLast(root.left);
        stack.addLast(root.right);
        while (!stack.isEmpty()) {
            TreeNode right = stack.pollLast();
            TreeNode left = stack.pollLast();

            // 如果两个节点都为空，继续下一次循环
            if (left == null && right == null) {
                continue;
            }
            // 如果一个节点为空，另一个节点不为空，则不对称
            if (left == null || right == null) {
                return false;
            }
            // 如果两个节点的值不相等，则不对称
            if (left.val != right.val) {
                return false;
            }
            stack.addLast(left.left);
            stack.addLast(right.right);

            stack.addLast(left.right);
            stack.addLast(right.left);
        }
        return true;
    }