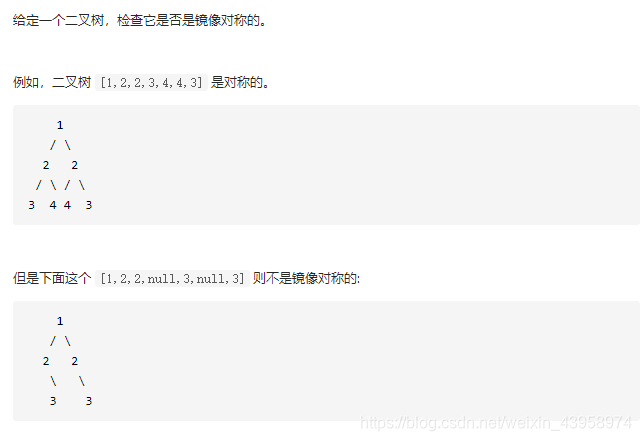
题目：对称二叉树

解题思路
对于二叉树的题目，一般都是递归解法。
如果题目变成：给两个二叉树，判断这两个二叉树是否为对称二叉树，相信大家很想到用递归来解决，从根节点一直递归到叶子节点进行比较。

而对于判断一个二叉树是否对称，不好直接递归判别函数isSymmetric()，需要借助一个辅助函数isSymmetricHelper()，辅助函数是判别两个二叉树是否为对称二叉树。
这样思路就很清晰了：

1. 首先将要判别的二叉树root作为参数传入判别函数isSymmetric()；
   • 先判别root是否为null,为空则返回true；只有不为空，才会有左右子树；
2. 将root的左右子树left和right作为参数，传入辅助函数isSymmetricHelper()；
   • 先设置一个递归终止条件（递归基），也就是越过叶子节点时的处理；
     • left和right中两者都为空，说明对称，返回true；
     • left和right中有一个为空，说明不对称了，返回false;
   • 对称判别条件，必须同时满足以下三个条件
     • left和right的val必须相同；
     • left的左子树必须和right的右子树对称，如何比较呢？调用isSymmetricHelper()；
     • left的右子树必须和right的左子树对称，如何比较呢？调用isSymmetricHelper()；

class Solution {
    //本方法：用来判断一个二叉树是否为对称二叉树
    public boolean isSymmetric(TreeNode root) {
        if(root == null) return true;
        return isSymmetricHelper(root.left, root.right);
    }
    //本方法：用来判别两个二叉树是否对称
    public boolean isSymmetricHelper(TreeNode r1, TreeNode r2){
        //递归基
        if(r1 == null && r2 == null) return true;
        if(r1 == null || r2 == null) return false;
        return r1.val == r2.val 
                && isSymmetricHelper(r1.left,r2.right) 
                && isSymmetricHelper(r1.right,r2.left);
    }
}