信用卡评分模型
项目简介
本文主要通过kaggle上Give me some credit数据进行数据分析，并根据信用评分建立原理，构建一个简易的信用评分卡模型。
数据来源
来自kaggle上的数据:https://www.kaggle.com/c/GiveMeSomeCredit/data
项目流程
-
理解数据
- 包括导入数据,查看数据集信息,从整体上了解数据
-
探索性数据分析和数据清洗
-
主要研究各个变量内部结构,自变量和因变量之间的关系
-
数据清洗
- 数据预处理(异常值和缺失值的处理)
- 特征工程(特征衍生,特征提取和特征选择)
-
-
构建模型(逻辑回归建立模型)
-
模型评估(ROC和AUC)
-
建立评分卡
项目过程
理解数据
- 导入数据/查看数据
import numpy as np
import pandas as pd
train=pd.read_csv('E:/机器学习/04_PythonCase/jupyterCase/02_data/cs-training.csv')
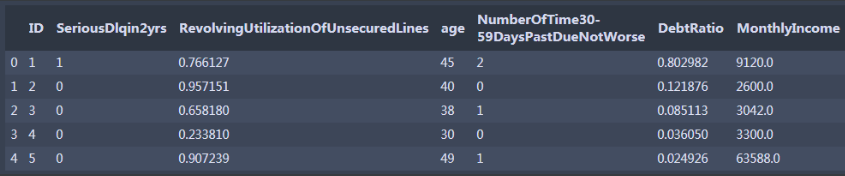
train.head()
#设置ID为索引
train.set_index('ID',inplace=True)
#查看数据大小和类型
print('数据大小：',train.shape)
print('数据类型：',train.dtypes)
#查看缺失情况
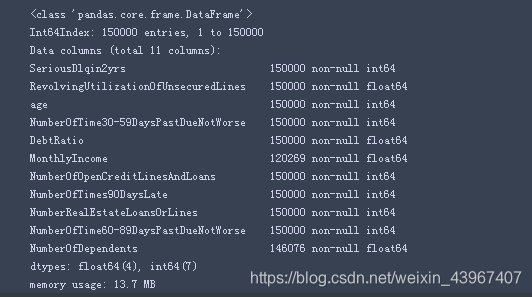
train,info()
可以看到NumberOfDependents和MonthlyIncome存在缺失
-
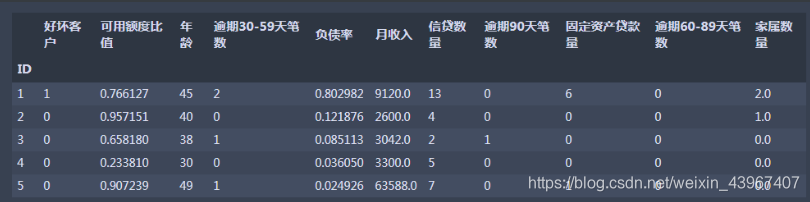
为了便于理解各个特征的含义,将特征名称更改为中文
#英文字段转换为中文字段 states={'SeriousDlqin2yrs':'好坏客户', 'RevolvingUtilizationOfUnsecuredLines':'可用额度比值', 'age':'年龄', 'NumberOfTime30-59DaysPastDueNotWorse':'逾期30-59天笔数', 'DebtRatio':'负债率', 'MonthlyIncome':'月收入', 'NumberOfOpenCreditLinesAndLoans':'信贷数量', 'NumberOfTimes90DaysLate':'逾期90天笔数', 'NumberRealEstateLoansOrLines':'固定资产贷款量', 'NumberOfTime60-89DaysPastDueNotWorse':'逾期60-89天笔数', 'NumberOfDependents':'家属数量'} #使用rename函数列的重列名 train.rename(columns=states,inplace=True) train.head()
- 查看各个特征的统计信息
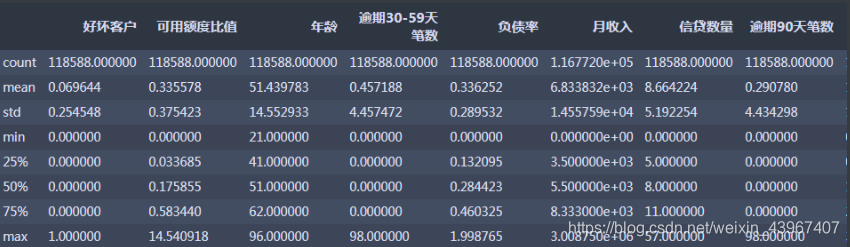
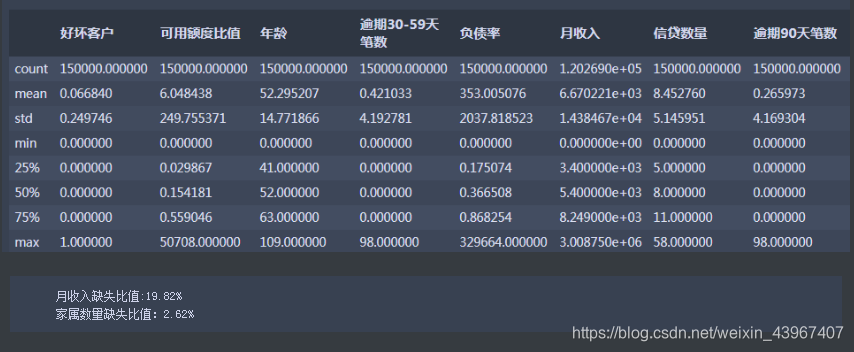
train.describe()
#查看缺失比
print('月收入缺失比值:%.2f%%'%(train[train['月收入'].isnull()].shape[0]/train.shape[0]*100))
print('家属数量缺失比值：%.2f%%'%(train[train['家属数量'].isnull()].shape[0]/train.shape[0]*100))
月收入缺失比比较大,后期需要处理
- 查看好坏客户分布情况
import seaborn as sns
sns.set_style('darkgrid', {'legend.frameon':True})
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
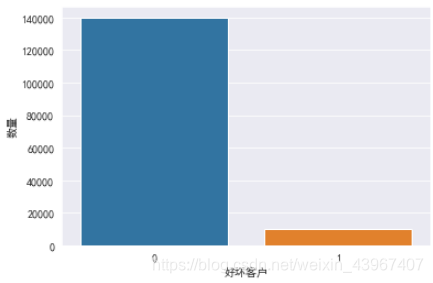
sns.countplot('好坏客户',data=train)
plt.ylabel('数量')
plt.show()
好坏客户分布不平衡,后期需要分箱,WOE编码处理
探索性数据分析和数据清洗
年龄
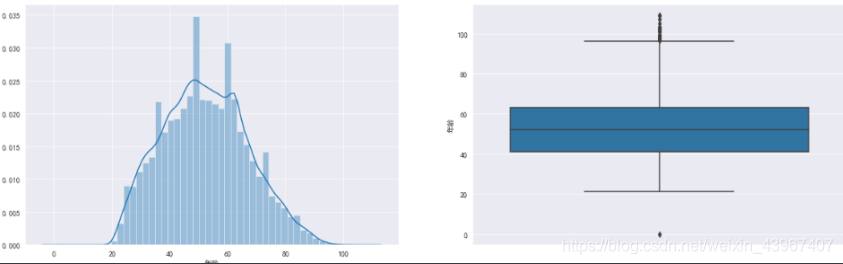
fig,[ax1,ax2]=plt.subplots(1,2,figsize=(20,6))
sns.distplot(train['年龄'],ax=ax1)
sns.boxplot(y='年龄',data=train,ax=ax2)
由图可知,年龄存在着离群值,用3倍标准差筛选数据
age_mean=train['年龄'].mean()
age_std=train['年龄'].std()
age_low=age_mean-3*age_std
age_up=age_mean+3*age_std
print('异常值下限:',age_low,'异常值上限',age_up)
## 筛选异常值
train=train[train['年龄']<age_up]
train=train[train['年龄']>age_low]
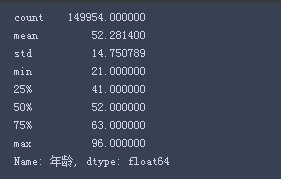
train['年龄'].describe()
- 查看不同年龄阶段的违约情况,[18,40),[40,60),[60,80),[80,97)
data_age=train.loc[:,['年龄','好坏客户']]
data_age.loc[(data_age['年龄']>=18)&(data_age['年龄']<40),'年龄']=1
data_age.loc[(data_age['年龄']>=40)&(data_age['年龄']<60),'年龄']=2
data_age.loc[(data_age['年龄']>=60)&(data_age['年龄']<80),'年龄']=3
data_age.loc[(data_age['年龄']>=80),'年龄']=4
age_isgb=data_age.groupby('年龄')['好坏客户'].sum()
age_total=data_age.groupby('年龄')['好坏客户'].count()
age_ratio=age_isgb/age_total
age_ratio.index
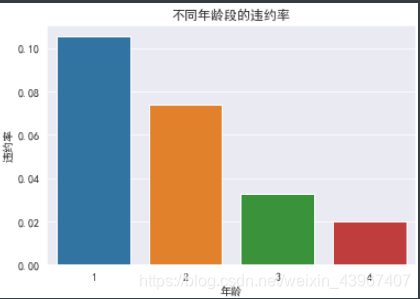
sns.barplot(x=age_ratio.index,y=age_ratio.values)
plt.title("不同年龄段的违约率")
plt.ylabel('违约率')
由图可以知道,年龄在18-40之间的违约情况最严重,随着年龄的增长,违约率逐渐降低
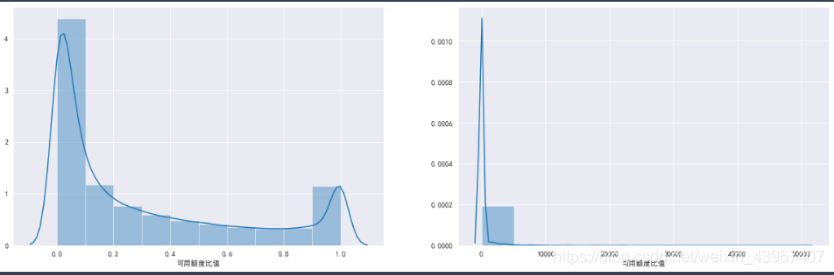
可用额度比值
#年龄-可用额度比值的散点图
figure=plt.figure(figsize=(8,6))
plt.scatter(train['可用额度比值'],train['年龄'])
plt.grid()
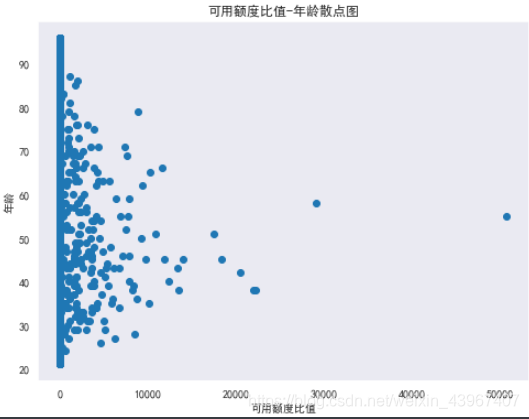
plt.title('可用额度比值-年龄散点图')
plt.xlabel('可用额度比值')
plt.ylabel('年龄')
理论上可用额度比值是小于1的,但是图示可知,可用额度比值超过10000的有多个,所以是否是异常值需要再深入确认
##四分位数观察异常值
sns.boxplot(data=train,y=train['可用额度比值'])
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hUTBCBz2-1569768518872)(E:\机器学习\05_Typora图片\1569764791119.png)]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvMDY0MDAzNWVhOTk1ODE2NzlmNjY3OTkwMWRmNjRhNzYucG5n)
###将数据分为两部分，大于1和小于1
data1=train.loc[train['可用额度比值']<1,'可用额度比值']
data2=train.loc[train['可用额度比值']>=1,'可用额度比值']
fig,[ax1,ax2]=plt.subplots(1,2,figsize=(20,6))
sns.distplot(data1,ax=ax1,bins=10)
sns.distplot(data2,ax=ax2,bins=10)
由图可以知道,可用额度比值大部分集中在0-1之间,超过1的大部分集中在1-5000之间,可再深入分析,得出划分异常值的临界数据
#将区间分为（0-1），(1-10),（10-20），（20-100），（100,1000），（1000-10000），（10000,51000）看一下违约率情况
data_r=train.loc[(train['可用额度比值']>=0)&(train['可用额度比值']<1),:]
is_1=data_r.loc[data_r['好坏客户']==1,:].shape[0]*100/data_r.shape[0]
data_r=train.loc[(train['可用额度比值']>=1)&(train['可用额度比值']<10),:]
is_2=data_r.loc[data_r['好坏客户']==1,:].shape[0]*100/data_r.shape[0]
data_r=train.loc[(train['可用额度比值']>=10)&(train['可用额度比值']<20),:]
is_3=data_r.loc[data_r['好坏客户']==1,:].shape[0]*100/data_r.shape[0]
data_r=train.loc[(train['可用额度比值']>=20)&(train['可用额度比值']<100),:]
is_4=data_r.loc[data_r['好坏客户']==1,:].shape[0]*100/data_r.shape[0]
data_r=train.loc[(train['可用额度比值']>=100)&(train['可用额度比值']<1000),:]
is_5=data_r.loc[data_r['好坏客户']==1,:].shape[0]*100/data_r.shape[0]
data_r=train.loc[(train['可用额度比值']>=1000)&(train['可用额度比值']<10000),:]
is_6=data_r.loc[data_r['好坏客户']==1,:].shape[0]*100/data_r.shape[0]
data_r=train.loc[(train['可用额度比值']>=10000)&(train['可用额度比值']<51000),:]
is_7=data_r.loc[data_r['好坏客户']==1,:].shape[0]*100/data_r.shape[0]
print('0-1违约率为：{0}%'.format(is_1),
'1-10违约率为：{0}%'.format(is_2),
'10-20违约率为：{0}%'.format(is_3),
'20-100违约率为：{0}%'.format(is_4),
'100-1000违约率为：{0}%'.format(is_5),
'1000-10000违约率为：{0}%'.format(is_6),
'10000-51000违约率为：{0}%'.format(is_7))
通过观察可知,10-20之间的违约率达到最大,1000-10000之间的违约率趋于正常(与0-1之间的违约率差不多),说明20是分界点,可以以20划分异常值和正常值
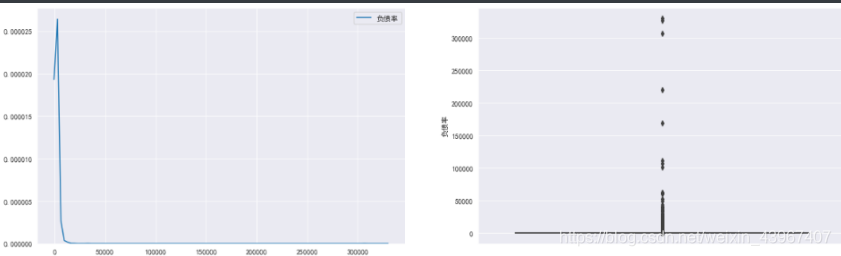
负债率
###负债率分析
sns.set_style('darkgrid', {'legend.frameon':True})
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
fig,[ax1,ax2]=plt.subplots(1,2,figsize=(20,6))
sns.kdeplot(train['负债率'],ax=ax1)
sns.boxplot(y=train['负债率'],ax=ax2)
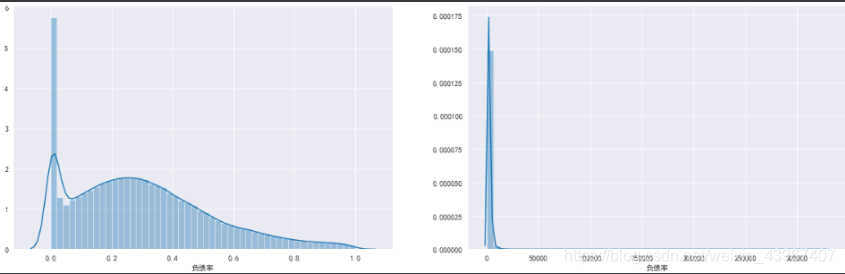
由图可知,负债率大部分集中在0-1之间,存在着离群值,可再细分分析
#将负债率划分为大于1和小于1
data1=train.loc[train['负债率']<1,'负债率']
data2=train.loc[train['负债率']>=1,'负债率']
fig,[ax1,ax2]=plt.subplots(1,2,figsize=(20,6))
sns.distplot(data1,ax=ax1)
sns.distplot(data2,ax=ax2)
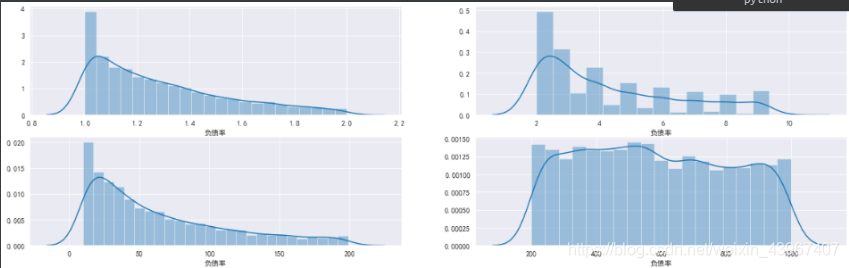
###多次细分[1,2），[2,10),[10,200），[200,1000）
data3=train.loc[(train['负债率']>=1)&(train['负债率']<2),'负债率']
data4=train.loc[(train['负债率']>=2)&(train['负债率']<10),'负债率']
data5=train.loc[(train['负债率']>=10)&(train['负债率']<200),'负债率']
data6=train.loc[(train['负债率']>=200)&(train['负债率']<1000),'负债率']
fig,[[ax1,ax2],[ax3,ax4]]=plt.subplots(2,2,figsize=(20,6))
sns.distplot(data3,ax=ax1)
sns.distplot(data4,ax=ax2)
sns.distplot(data5,ax=ax3)
sns.distplot(data6,ax=ax4)
可看到负债率数值大小在200-1000之间的数据分布较为平衡
###查看各个区间违约率情况
debt1=train.loc[(train['负债率']>0)&(train['负债率']<1),:]
DebIs_1=debt1.loc[debt1['好坏客户']==1,:].shape[0]*100/debt1.shape[0]
debt2=train.loc[(train['负债率']>=1)&(train['负债率']<2),:]
DebIs_2=debt2.loc[debt2['好坏客户']==1,:].shape[0]*100/debt2.shape[0]
debt3=train.loc[(train['负债率']>=2)&(train['负债率']<10),:]
DebIs_3=debt3.loc[debt3['好坏客户']==1,:].shape[0]*100/debt3.shape[0]
debt4=train.loc[(train['负债率']>=10)&(train['负债率']<200),:]
DebIs_4=debt4.loc[debt4['好坏客户']==1,:].shape[0]*100/debt4.shape[0]
debt5=train.loc[(train['负债率']>=200)&(train['负债率']<1000),:]
DebIs_5=debt5.loc[debt5['好坏客户']==1,:].shape[0]*100/debt5.shape[0]
print('0-1违约率为：{0}%'.format(DebIs_1),
'1-2违约率为：{0}%'.format(DebIs_2),
'2-10违约率为：{0}%'.format(DebIs_3),
'10-200违约率为：{0}%'.format(DebIs_4),
'200-1000违约率为：{0}%'.format(DebIs_5))
可以看到,1-2之间的违约率达到最大,说明负债率可以以2为分隔界限
train=train[train['负债率']<2]
train.describe()
信贷数量
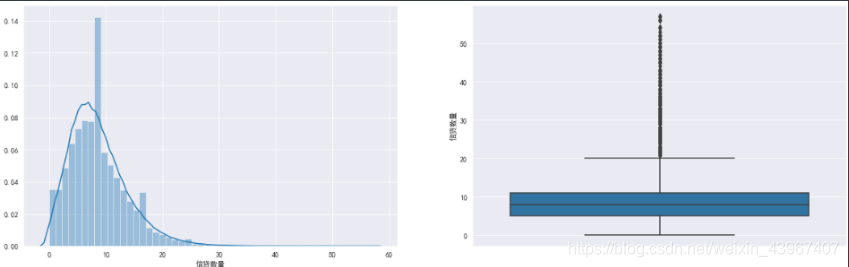
fig,[ax1,ax2]=plt.subplots(1,2,figsize=(20,6))
sns.distplot(train['信贷数量'],ax=ax1)
sns.boxplot(y=train['信贷数量'],ax=ax2)
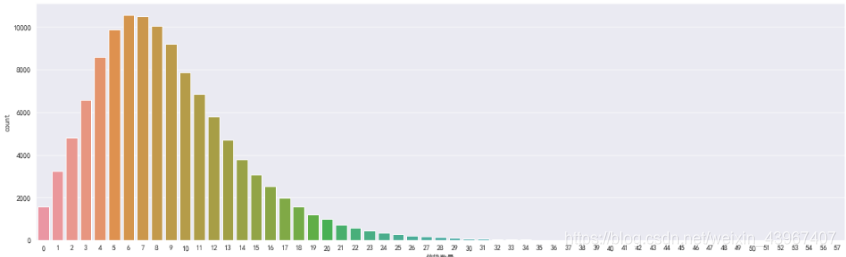
fig=plt.figure(figsize=(20,6))
sns.countplot(train['信贷数量'])
train.loc[train['信贷数量']>36,'信贷数量']=36
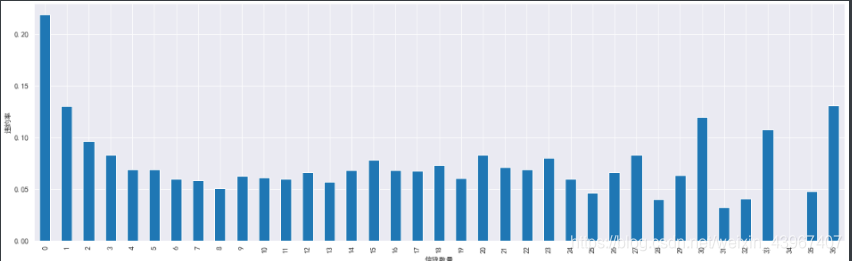
d1=train.groupby(['信贷数量'])['好坏客户'].sum()
total=train.groupby(['信贷数量'])['好坏客户'].count()
r=d1/total
r.plot(kind='bar',figsize=(20,6))
可以看到信贷数量分布较为均衡,说明可能没有异常值,不需要特殊处理
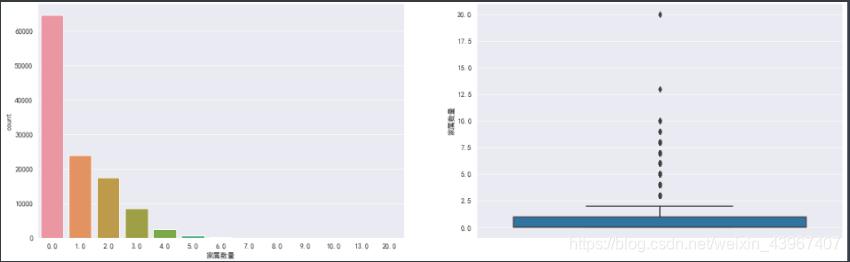
家属数量
###家属数量分析
fig,[ax1,ax2]=plt.subplots(1,2,figsize=(20,6))
sns.countplot(train['家属数量'],ax=ax1)
sns.boxplot(y=train['家属数量'],ax=ax2)
ratio=train[train['家属数量'].isnull()].shape[0]/train.shape[0]
print('家属数量缺失比值%.2f%%'%(ratio*100))
print(train[train['家属数量'].isnull()].shape[0])
家属数量缺失比为0.4%,缺失数量较少,可以直接删除
train=train[train['家属数量'].isnull()==False]
train.info()
月收入
###月收入分析
ratio=train[train['月收入'].isnull()].shape[0]/train.shape[0]
print('月收入缺失比值%.2f%%'%(ratio*100))
print('缺失数量',train[train['月收入'].isnull()].shape[0])
月收入缺失值较多,用随机森林填充
###月收入缺失值比较多，用随机森林预测填充
from sklearn.ensemble import RandomForestRegressor
X_df=train[train['月收入'].notnull()]
X=X_df.iloc[:,[1,2,3,4,6,7,8,9,10]]
Y=X_df['月收入']
X_test=train[train['月收入'].isnull()].iloc[:,[1,2,3,4,6,7,8,9,10]]
print(X.shape,Y.shape,X_test.shape)
##随机森林预测
#n_estimators:弱学习器的最大迭代次数
rfr = RandomForestRegressor(random_state=0, n_estimators=200,max_depth=3,n_jobs=-1)
rfr.fit(X,Y)
pre_Y=rfr.predict(X_test)
train.loc[train['月收入'].isnull(),'月收入']=pre_Y
train.info()
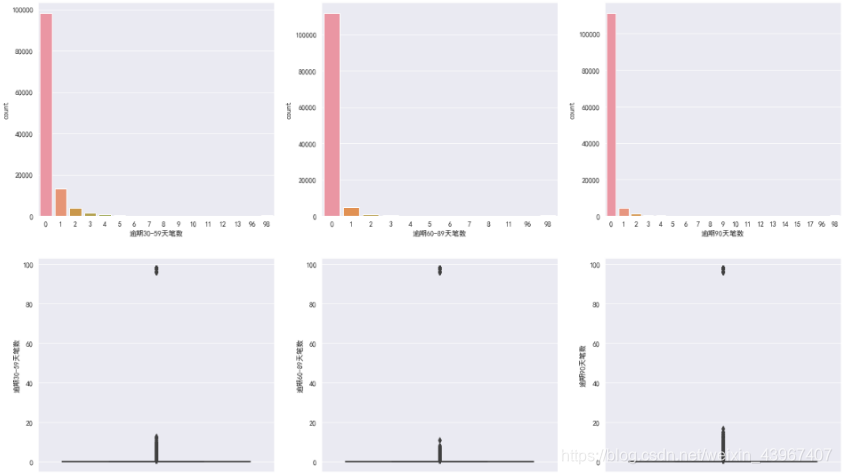
逾期天数
fig,[[ax1,ax2,ax3],[ax4,ax5,ax6]]=plt.subplots(2,3,figsize=(20,12))
sns.countplot(train['逾期30-59天笔数'],ax=ax1)
sns.countplot(train['逾期60-89天笔数'],ax=ax2)
sns.countplot(train['逾期90天笔数'],ax=ax3)
sns.boxplot(y=train['逾期30-59天笔数'],ax=ax4)
sns.boxplot(y=train['逾期60-89天笔数'],ax=ax5)
sns.boxplot(y=train['逾期90天笔数'],ax=ax6)
可以看出,超过90的为明显异常值,直接删除
train=train[train['逾期30-59天笔数']<90]
train=train[train['逾期60-89天笔数']<90]
train=train[train['逾期90天笔数']<90]
特征衍生
#特征衍生
train['总逾期数']=train['逾期30-59天笔数']+train['逾期60-89天笔数']+train['逾期90天笔数']
train['月支出']=train['负债率']*train['月收入']
train['总人数']=train['家属数量']+1 #原来数据中的家属数量不包括本人
##类型转换
train.dtypes
train['家属数量']=train['家属数量'].astype('int64')
train['总人数']=train['总人数'].astype('int64')
train['月收入']=train['月收入'].astype('int64')
train['月支出']=train['月支出'].astype('int64')
特征分箱
#可用额度比值分箱
train.loc[train['可用额度比值']<=1,'可用额度比值']=0
train.loc[(train['可用额度比值']>1)&(train['可用额度比值']<=20),'可用额度比值']=1
train.loc[train['可用额度比值']>20,'可用额度比值']=2
#负债率分箱
train.loc[train['负债率']<1,'负债率']=0
train.loc[(train['负债率']>=1)&(train['负债率']<2),'负债率']=1
train.loc[train['负债率']>=2,'负债率']=2
# 逾期天数分箱
train.loc[train['逾期30-59天笔数']>=8,'逾期30-59天笔数']=8
train.loc[train['逾期60-89天笔数']>=7,'逾期30-59天笔数']=7
train.loc[train['逾期90天笔数']>=10,'逾期30-59天笔数']=10
train.loc[train['总逾期数']>1,'总逾期数']=1
#家属数量分箱
train.loc[train['家属数量']>=7,'家属数量']=7
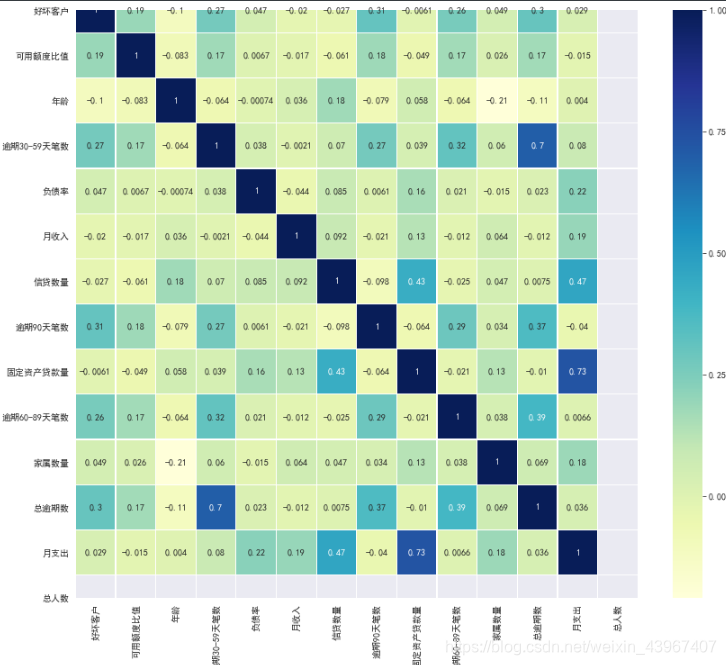
特征选择
###查看各个特征之间的相关系数
corr=train.corr()
plt.figure(figsize=(14,12))
sns.heatmap(corr,annot=True,linewidth=0.2,cmap='YlGnBu')
WOE/IV值计算
def bin_woe(tar,var,n=None,cat=None):
"""
连续自变量分箱,woe,iv变换
tar:target目标变量
var:进行woe,iv转换的自变量
n:分组数量
"""
total_bad=tar.sum()
total_good=tar.count()-tar.sum()
totalRate=total_good/total_bad
if cat=='s':
msheet=pd.DataFrame({tar.name:tar,var.name:var,'var_bins':pd.qcut(var,n,duplicates='drop')})
grouped = msheet.groupby(['var_bins'])
elif (cat == 'd') and (n is None):
msheet = pd.DataFrame({tar.name:tar,var.name:var})
grouped = msheet.groupby([var.name])
groupBad = grouped.sum()[tar.name]
groupTotal = grouped.count()[tar.name]
groupGood = groupTotal - groupBad
groupRate = groupGood/groupBad
groupBadRate = groupBad/groupTotal
groupGoodRate = groupGood/groupTotal
woe = np.log(groupRate/totalRate)
iv = np.sum((groupGood/total_good-groupBad/total_bad)*woe)
if cat == 's':
new_var, cut = pd.qcut(var, n, duplicates='drop',retbins=True, labels=woe.tolist())
elif cat == 'd':
dictmap = {}
for x in woe.index:
dictmap[x] = woe[x]
new_var, cut = var.map(dictmap), woe.index
return woe.tolist(), iv, cut, new_var
# 确定变量类型，连续变量(s)还是离散变量(d)
dvar = ['可用额度比值','负债率','逾期30-59天笔数', '逾期60-89天笔数','逾期90天笔数','总逾期数','Withdepend',
'固定资产贷款量','家属数量']
svar = ['月收入','年龄','月支出','信贷数量']
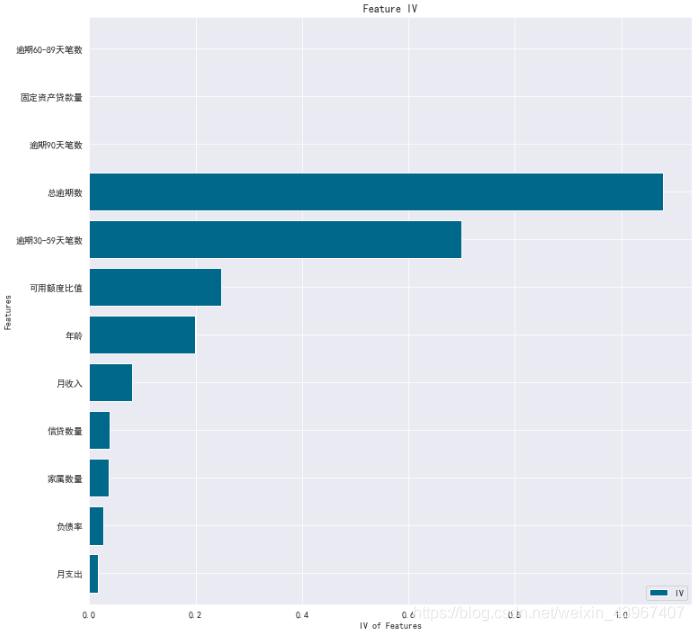
# 可视化woe得分和iv得分
def woe_vs(data):
cutdict = {}
ivdict = {}
woe_dict = {}
woe_var = pd.DataFrame()
for var in data.columns:
if var in dvar:
woe, iv, cut, new = bin_woe(data['好坏客户'], data[var], cat='d')
woe_dict[var] = woe
woe_var[var] = new
ivdict[var] = iv
cutdict[var] = cut
elif var in svar:
woe, iv, cut, new = bin_woe(data['好坏客户'], data[var], n=5, cat='s')
woe_dict[var] = woe
woe_var[var] = new
ivdict[var] = iv
cutdict[var] = cut
ivdict = sorted(ivdict.items(), key=lambda x:x[1], reverse=False)
iv_vs = pd.DataFrame([x[1] for x in ivdict],index=[x[0] for x in ivdict],columns=['IV'])
ax = iv_vs.plot(kind='barh',
figsize=(12,12),
title='Feature IV',
fontsize=10,
width=0.8,
color='#00688B')
ax.set_ylabel('Features')
ax.set_xlabel('IV of Features')
return ivdict, woe_var, woe_dict, cutdict
# woe转化
ivinfo, woe_data, woe_dict, cut_dict = woe_vs(train)
筛选出IV值大于0.1的特征,这些特征具有较大的预测能力,这些特征是年龄,可用额度比值,逾期30-59天笔数,总逾期数,其中总逾期数和逾期30-59天的相关系数为0.7,具有强相关性,因此选择总逾期数输入模型
#筛选出IV>0.1的特征
# 年龄,可用额度比值,总逾期数,逾期30-59天笔数
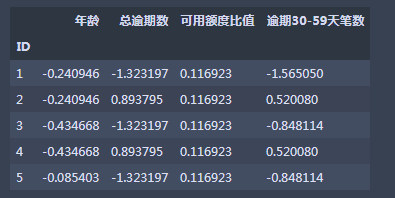
X=woe_data.loc[:,['年龄','总逾期数','可用额度比值','逾期30-59天笔数']]
y=train['好坏客户']
X.head()
构建模型
#划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=42)
#训练模型(逻辑回归)
from sklearn.linear_model import LogisticRegression
model=LogisticRegression(random_state=0,
solver="sag",
penalty="l2",
class_weight="balanced",
C=1.0,
max_iter=500)
model.fit(X_train, y_train)
model_proba = model.predict_proba(X_test)#predict_proba返回的结果是一个数组，包含两个元素，第一个元素是标签为0的概率值，第二个元素是标签为1的概率值
model_score=model_proba[:,1]
模型评估
#用ROC曲线和AUC来评估模型的预测能力
from sklearn.metrics import roc_curve, roc_auc_score
fpr,tpr,thresholds =roc_curve(y_test,model_score)
auc_score=roc_auc_score(y_test,model_score)
plt.plot(fpr, tpr, linewidth=2, label='AUC = %0.2f'%auc_score)
plt.plot([0,1],[0,1], "k--")
plt.axis([0,1,0,1])
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.legend()
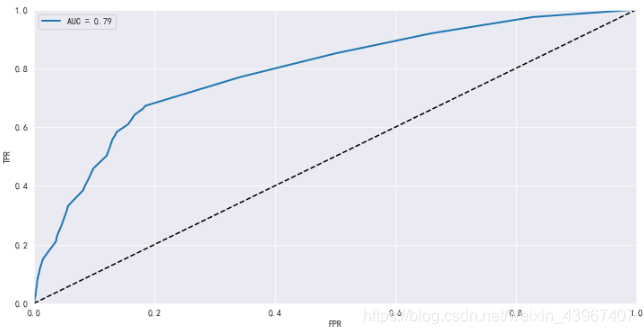
可以看到AUC是0.79,说明模型区分能力良好
制作评分卡
s
c
o
r
e
=
A
−
B
l
o
g
(
o
d
d
s
)
=
A
−
B
(
β
0
+
β
1
x
1
+
β
2
x
2
+
.
.
.
+
β
n
x
n
)
score=A-Blog(odds)=A-B(\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_nx_n)
score=A−Blog(odds)=A−B(β0+β1x1+β2x2+...+βnxn)
B
=
P
D
O
l
o
g
(
2
)
B=\frac{PDO}{log(2)}
B=log(2)PDO
A
=
P
0
+
B
l
o
g
(
β
0
)
A=P_0+Blog(\beta_0)
A=P0+Blog(β0)
IV_info=['年龄','总逾期数','可用额度比值','逾期30-59天笔数']
intercept=model.intercept_
coef=model.coef_
coe=coef[0].tolist()
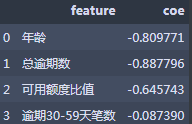
coe_df=pd.DataFrame({'feature':IV_info,'coe':coe})
coe_df
import math
B=20/math.log(2)
A=600+B*math.log(1/20)
#基础分
score=round(A-B*intercept[0],0)
featurelist = []
woelist = []
cutlist = []
for k,v in woe_dict.items():
if k in IV_info:
for n in range(0,len(v)):
featurelist.append(k)
woelist.append(v[n])
cutlist.append(cut_dict[k][n])
scoreboard = pd.DataFrame({'feature':featurelist,'woe':woelist,'cut':cutlist},
columns=['feature','cut','woe'])
score_df=pd.merge(scoreboard,coe_df)
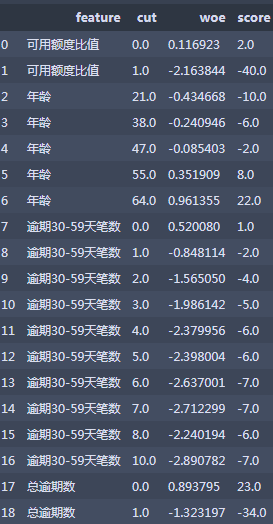
score_df['score']=round(-B*score_df['woe']*score_df['coe'],0)
score_df.drop('coe',axis=1,inplace=True)
score_df
结论
- 本次建模AUC为0.79,识别能力良好,后期可通过网格搜索超参数获取更好的结果,欢迎指正