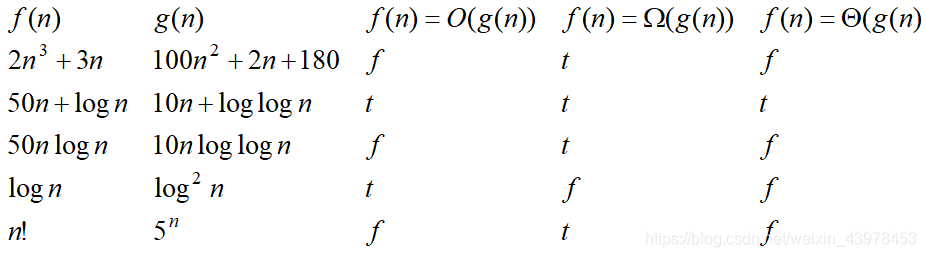无论在以后找工作还是面试中,都离不开算法设计与分析。本博文总结了相关算法设计的题目,旨在帮助加深对贪心算法、动态规划、回溯等算法的理解。
1、计算下述算法执行的加法次数:
输入:n=2^t //t为整数
输出:加法次数 k
K=0
while n>=1 do
for j=1 to n do
k:= k+1
n= n/2
return k
解析:第一次循环执行n次加法,第二次循环执行1/2次加法,第三次循环执行1/ 2 2 = 1 / 4 2^2=1/4 22=1/4次加法…因此,上述算法执行加法的次数为 n + 1 2 n + 1 4 n + . . . + 1 n+\frac{1}{2}n+\frac{1}{4}n+...+1 n+21n+41n+...+1= n + n − 1 2 n + 1 2 n − 1 4 n + . . . . − 1 n+n-\frac{1}{2}n+\frac{1}{2}n-\frac{1}{4}n+....-1 n+n−21n+21n−41n+....−1=2n-1
2、考虑下面每对函数 f(n) 和 g(n) ,如果它们的阶相等则使用Θ记号,否则使用 O 记号表示它们的关系
f ( n ) = ( n 2 − n ) / 2 , g ( n ) = 6 n f(n)=(n^2-n)/2,g(n)=6n f(n)=(n2−n)/2,g(n)=6n
解析:
前导知识:
1 < l o g n < n < n l o g n < n 2 < n 3 < 2 n < n ! < n n 1<logn<n<nlogn<n^2<n^3<2^n<n!<n^n 1<logn<n<nlogn<n2<n3<2n<n!<nn
g ( n ) = O ( f ( n ) ) g(n)=O(f(n)) g(n)=O(f(n)),因为 f ( n ) = Θ ( n 2 ) , g ( n ) = Θ ( n ) f(n)=\Theta(n^2),g(n)=\Theta(n) f(n)=Θ(n2),g(n)=Θ(n)
f ( n ) = n + 2 n , g ( n ) = n 2 f(n)=n+2\sqrt{n},g(n)=n^2 f(n)=n+2n,g(n)=n2
解析: f ( n ) = O ( g ( n ) ) f(n)=O(g(n)) f(n)=O(g(n)),因为 f ( n ) = Θ ( n ) , g ( n ) = Θ ( n 2 ) f(n)=\Theta(n),g(n)=\Theta(n^2) f(n)=Θ(n),g(n)=Θ(n2)
f ( n ) = n + n l o g n , g ( n ) = n n f(n)=n+nlogn,g(n)=n\sqrt{n} f(n)=n+nlogn,g(n)=nn
解析: f ( n ) = O ( g ( n ) ) f(n)=O(g(n)) f(n)=O(g(n)),因为 f ( n ) = Θ ( n l o g n ) , g ( n ) = Θ ( n 3 2 ) f(n)=\Theta(nlogn),g(n)=\Theta(n^\frac{3}{2}) f(n)=Θ(nlogn),g(n)=Θ(n23)
f ( n ) = 2 ( l o g n ) 2 , g ( n ) = l o g n + 1 f(n)=2(log^n)^2,g(n)=logn+1 f(n)=2(logn)2,g(n)=logn+1
解析: g ( n ) = O ( f ( n ) ) g(n)=O(f(n)) g(n)=O(f(n))
f ( n ) = l o g ( n ! ) , g ( n ) = n 1.05 f(n)=log(n!),g(n)=n^{1.05} f(n)=log(n!),g(n)=n1.05
解析: f ( n ) = O ( g ( n ) ) f(n)=O(g(n)) f(n)=O(g(n))
3、在表1.1中填入 true 或 false
解析:利用上题的前导知识就可以得出。
4、对于下面每个函数 f(n),用f(n) =Θ(g(n))的形式,其中g(n)要尽可能简洁,然后按阶递增序排列它们(最后一列)
( n − 2 ) ! = Θ ( ( n − 2 ) ! ) (n-2)!=\Theta((n-2)!) (n−2)!=Θ((n−2)!)
5 l o g ( n + 100 ) 10 = Θ ( l o g n ) 5log(n+100)^{10}=\Theta(logn) 5log(n+100)10=Θ(logn)
2 2 n = Θ ( 4 n ) 2^{2n}=\Theta(4^n) 22n=Θ(4n)
0.001 n 4 + 3 n 3 + 1 = Θ ( n 4 ) 0.001n^4+3n^3+1=\Theta(n^4) 0.001n4+3n3+1=Θ(n4)
( l n n ) 2 = Θ ( l n 2 n ) (ln n)^2=\Theta(ln^2n) (lnn)2=Θ(ln2n)
n 3 + l o g n = Θ ( n 3 ) \sqrt[3]n+logn=\Theta(\sqrt[3]n) 3n+logn=Θ(3n)
3 n = Θ ( 3 n ) 3^n=\Theta(3^n) 3n=Θ(3n)
l o g ( n ! ) = Θ ( n l o g n ) log(n!)=\Theta(nlogn) log(n!)=Θ(nlogn)
l o g ( n n + 1 ) = Θ ( n l o g n ) log(n^{n+1})=\Theta(nlogn) log(nn+1)=Θ(nlogn)
1 + 1 2 + . . . . + 1 n = Θ ( l o g n ) 1+\frac{1}{2}+....+\frac{1}{n}=\Theta(logn) 1+21+....+n1=Θ(logn)
解析:最后一个用到了调和公式: ∑ k = 1 n 1 k = l o g n + O ( 1 ) \sum_{k=1}^{n}\frac{1}{k}=logn+O(1) ∑k=1nk1=logn+O(1)
按阶递增的顺序排列:
1 + 1 2 + . . . . + 1 n 1+\frac{1}{2}+....+\frac{1}{n} 1+21+....+n1、 5 l o g ( n + 100 ) 10 5log(n+100)^{10} 5log(n+100)10、 ( l n n ) 2 (ln n)^2 (lnn)2、 n 3 + l o g n \sqrt[3]n+logn 3n+logn、 l o g ( n ! ) log(n!) log(n!)、 l o g ( n n + 1 ) log(n^{n+1}) log(nn+1)、 0.001 n 4 + 3 n 3 + 1 0.001n^4+3n^3+1 0.001n4+3n3+1、 3 n 3^n 3n、 2 2 n 2^{2n} 22n、 ( n − 2 ) ! (n-2)! (n−2)!
5、求解递推方程
前导知识:主定理
前导知识:递归树:
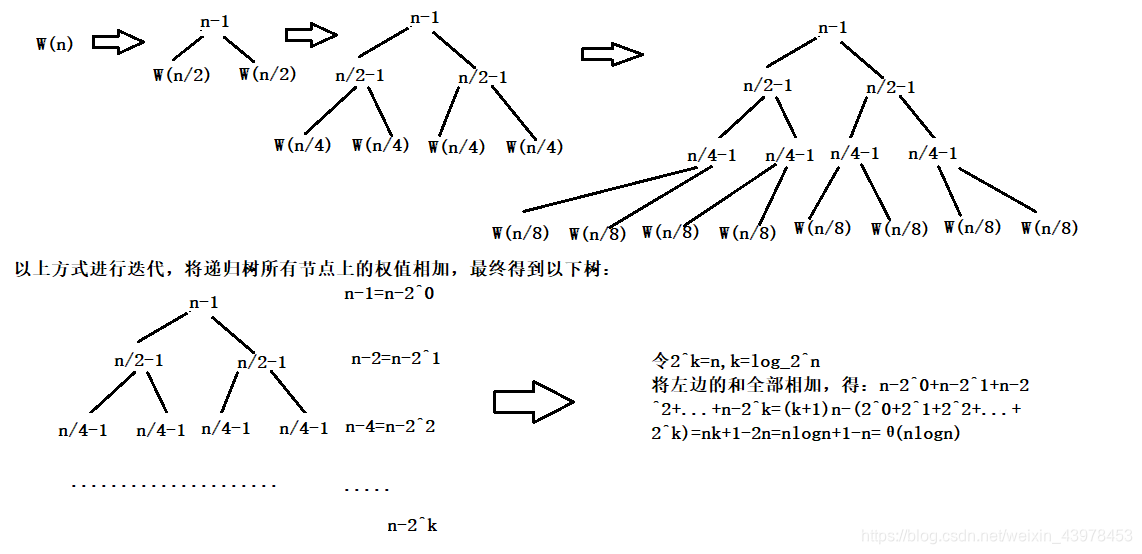
例子:递归树是一棵节点带权的二叉树,初始递归树只有一个结点,标记为权重W(n),然后不断进行迭代,最后直到树种不再含有权为函数的结点为止,然后将树根结点到树叶节点的全部权值加起来,即为算法的复杂度。以二路归并排序算法的递推方程为例子进行递归树讲解。
已知 W ( n ) = 2 W ( n / 2 ) + n − 1 W(n)=2W(n/2)+n−1 W(n)=2W(n/2)+n−1,并且W(1)=0,递归树求解过程如下图:
(1) T ( n ) = T ( n − 1 ) + n 2 , T ( 1 ) = 1 T(n)=T(n-1)+n^2,T(1)=1 T(n)=T(n−1)+n2,T(1)=1
解析:
T ( n − 1 ) = T ( n − 2 ) + ( n − 1 ) 2 T(n-1)=T(n-2)+(n-1)^2 T(n−1)=T(n−2)+(n−1)2
T ( n − 2 ) = T ( n − 3 ) + ( n − 2 ) 2 T(n-2)=T(n-3)+(n-2)^2 T(n−2)=T(n−3)+(n−2)2
T ( n − 3 ) = T ( n − 4 ) + ( n − 3 ) 2 T(n-3)=T(n-4)+(n-3)^2 T(n−3)=T(n−4)+(n−3)2
…
因此,将上述各式相加,得到 T ( n ) = 1 + 2 2 + 3 3 + . . . + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 T(n)=1+2^2+3^3+...+n^2=\frac{n(n+1)(2n+1)}{6} T(n)=1+22+33+...+n2=6n(n+1)(2n+1)
(2) T ( n ) = 9 T ( n / 3 ) + n , T ( 1 ) = 1 T(n)=9T(n/3)+n,T(1)= 1 T(n)=9T(n/3)+n,T(1)=1
解析: a = 9 , b = 3 a=9,b=3 a=9,b=3,因此, n l o g b a = n l o g 3 9 = n 2 , f ( n ) = n n^{log_b^a}=n^{log_3^9}=n^2,f(n)=n nlogba=nlog39=n2,f(n)=n
因为, f ( n ) < O ( n 2 ) f(n)<O(n^2) f(n)<O(n2),因此, T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
(3) T ( n ) = T ( n / 2 ) + T ( n / 4 ) + c n , T ( 1 ) = 1 T(n)=T(n/2) + T(n/4) +cn,T(1)=1 T(n)=T(n/2)+T(n/4)+cn,T(1)=1
解析:
(3) T ( n ) = 5 T ( n / 2 ) + ( n l o g n ) 2 , T ( 1 ) = 1 T(n)=5T(n/2) + (nlogn)^2,T(1)=1 T(n)=5T(n/2)+(nlogn)2,T(1)=1
解析: a = 5 , b = 2 , n l o g b a = n l o g 2 5 , f ( n ) = ( n l o g n ) 2 a=5,b=2,n^{log_b^a}=n^{log_2^5},f(n)=(nlogn)^2 a=5,b=2,nlogba=nlog25,f(n)=(nlogn)2,由于, n l o g 2 5 > O ( f ( n ) ) n^{log_2^5}>O(f(n)) nlog25>O(f(n)),因此,T(n)= O ( n l o g 2 5 ) O(n^{log_2^5}) O(nlog25)
5、设A是 n 个非0实数构成的数组,设计一算法重排数组的数,使得负数都在正数的前面。
要求时间、空间复杂性为 O(n)和O(1)
解析:由于时间复杂度为O(n),空间复杂度为O(1),说明只需要遍历一次数组,不需要额外的存储空间,就能完成该问题的求解。
算法:
- 从右向左扫描直到找到第一个负数A[p]
- 从左向右扫描直到找到第一个正数A[q]
- 若p>q,则交换A[p]、A[q]
- 若p<=q,则停止,否则重复上述步骤
6、给定含 n 个不同的数的数组 L = < X 1 , … , X n L=<X_1,…,X_n L=<X1,…,Xn>. 如果 L 中存在 X i X_i Xi 使 x 1 < x 2 < … < X i > X i + 1 > … > x n x_1<x_2<…<X_i>X_i+1>…>x_n x1<x2<…<Xi>Xi+1>…>xn 则说 L 是单峰的,并称 x i x_i xi 是 L的峰顶。假设 L 是单峰的,设计算法找到 L 的峰顶。
解析:用二分法:
- 若|L|=3,则L[2]即为所求
- 若|L|>3,则取k=[n/2],检查若L[k-1]<L[k]>L[k+1],则找到
- 否则,若L[k-1]<L[k]<L[k+1],说明单峰在右边,若L[k-1]>L[k]>L[k+1],说明单峰在左边,继续进行二分查找
7、设A 是 n 个不同的数排好序的数组,给定数 L 和 U , L<U, 设计算法找到A 中满足 L<x<U 的所有 x。
解析:一般对于已经排好序的数组相关的算法,可以想想是否可以用到二分算法。
使用二分查找:
- 用二分查找法找到等于或大于L的最小的位置k,等于的情况k+1(因为题目要求的是大于)
- 类似的用二分查找找到等于或小于U的最大数的位置j(等于的情况j-1)
- 输出从k到j的数
8、用动态规划算法求解下面的组合优化问题:
m a x { g 1 ( x 1 ) + g 2 ( x 2 ) + g 3 ( x 3 ) } max\{g_1(x_1)+g_2(x_2)+g_3(x_3)\} max{
g1(x1)+g2(x2)+